一、題目解析

1、需返回排序好的第k個最大元素
2、要求時間復雜度為O(N)
二、算法原理
解法1:堆排序(大根堆) k*O(N)
借用大堆的性質,將元素插入到大堆中,按照k輸出堆頂第k個元素
解法2:堆排序(小根堆) (N-k)*O(logN)
先建k個小堆,然后插入元素,依次與堆頂元素比較,比堆頂元素大,則pop(刪除堆頂元素)掉堆頂元素,插入nums[i],最終小堆中存儲前k個最大的數
解法3:分治-快排 O(N)
基于數組分三塊+隨機數選擇元素
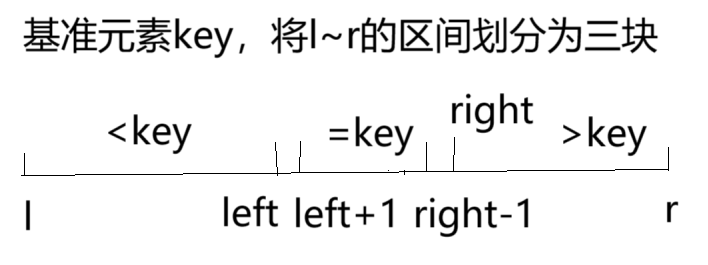
通過埋下隨機數種子srand(time(NULL)),rand() % (right-left+1) + left,找到隨機數下標,得到基準元素key
由i移動遍歷數組,left = -1,right = nums.size()+1,如果nums[i]<key,? ? swap(nums[i++],nums[++left]);如果nums[i] == key,i++;如果nums[i]>key,swap(nums[i],nums[--right])
依據排序好的數組,統計區間各個元素的個數判斷情況

三、代碼示例
解法1:
int findKthLargest(vector<int>& nums, int k){sort(nums.begin(),nums.end(),greater<int>());return nums[k-1];// O(N)//大堆priority_queue<int> pq(nums.begin(),nums.end());while(--k){pq.pop();}return pq.top();//K*logN}
解法2:
int findKthLargest(vector<int>& nums, int k){//小堆//(N-K)*logNpriority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k);//建k個數的小堆for(int i = k;i < nums.size();i++){if(nums[i] > pq.top()){pq.pop();pq.push(nums[i]);}}return pq.top();}
解法3:
int findKthLargest(vector<int>& nums, int k){//快排srand(time(NULL));return qsort(nums,0,nums.size()-1,k);}int qsort(vector<int>& nums,int l,int r,int k){if(l == r) return nums[l];//隨機選擇基準元素int key = getRandom(nums,l,r);//基準元素分三塊int left = l-1,right = r+1,i = l;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i] == key) i++;else swap(nums[i],nums[--right]);}//分情況討論int c = r - right +1,b = right - left - 1;if(c>=k) return qsort(nums,right,r,k);else if(b+c>=k) return key;else return qsort(nums,l,left,k-b-c);}int getRandom(vector<int>& nums,int left,int right){return nums[rand() % (right - left + 1) + left];}
看到最后,如果對您有所幫助,還請點贊、收藏和關注,我們下期再見!







)

)









)





