目錄

前言：

1、二叉搜索樹的概念

2、二叉搜索樹性能分析

3、二叉搜索樹的實現

BinarySelectTree.h

test.cpp

4、key 和 key / value（ map 和 set 的鋪墊 ）?

---

前言：

? 又回到數據結構了，這次我們將要學習一些復雜的數據結構，例如 map，set，multimap，multiset 和紅黑樹，AVL樹等，而這些復雜數據結構的基礎都是二叉搜索樹，避免大家沒有聽過這個玩意，今天咱們來單獨講一講二叉搜索樹。

1、二叉搜索樹的概念

?二叉搜索樹又稱二叉排序樹（因為二叉搜索樹中序遍歷的結果是從小到大排序的），它或者是一棵空樹，或者是具有以下性質的二叉樹:

? 若它的左子樹不為空，則左子樹上所有結點的值都小于等于根結點的值

? 若它的右子樹不為空，則右子樹上所有結點的值都大于等于根結點的值

? 它的左右子樹也分別為二叉搜索樹

? 二叉搜索樹中可以支持插入相等的值，也可以不支持插入相等的值，具體看使用場景定義，后續我們學習map/set/multimap/multiset系列容器底層就是二叉搜索樹，其中map/set不支持插入相等 值(所以在需要去重的算法題中 set 和 map 是很好用的)，multimap/multiset支持插入相等值。

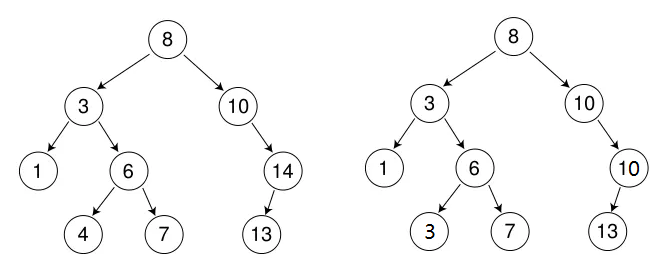
?下面我實現的二叉搜索樹就是以左邊的樹作為例子進行增刪查操作的。

2、二叉搜索樹性能分析

? 由于二叉搜索樹每一層只會選擇左節點和右節點中的一個比較大小，所以正常情況下性能為其高度。

? 最優情況下：二叉樹是一棵完全二叉樹，那么此時，每次搜索都能排除一半情況，此時高度為logN，所以搜索時間復雜度為O（logN）。

? 最壞情況下：二叉樹的所有結點都放在一條分叉上，此時高度最高，為N，此時時間復雜度為O（N）。

? 所以綜合而言，二叉搜索樹增刪查的時間復雜度為O（N），二叉搜索樹一般不支持改，因為一改二叉搜素樹就混亂了。

? 由于當出現一個分叉的情況時，時間復雜度有點高，所以就出現了平衡二叉樹這一做法，這個比較復雜，后面AVL樹和紅黑樹會講。

? 其實二分查找時間復雜度也是O（logN），但是缺陷也很大：

1、首先下標要滿足隨機訪問，而且必須有序。

2、其次插入和刪除效率太低了，刪除或插入一個數據需要挪動一堆數據。

到這里二叉搜索樹的基礎知識就結束了，下面我們來實現一下這個簡單的數據結構吧。

3、二叉搜索樹的實現

我們分兩個文件來寫，代碼中給出了注釋：

BinarySelectTree.h

#define _CRT_SECURE_NO_WARNINGS 1#include <iostream>
#include <algorithm>
using namespace std;template <class K>
class BSTreeNode
{
public:K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){ }
};template <class K>
class BSTree
{
public:typedef BSTreeNode<K> Node;BSTree() = default;//由于我們已經有了拷貝構造，所以不寫構造函數就會報錯（因為缺少默認構造），//而這個類沒必要寫構造，這個句子就是告訴編譯器構造函數交給你默認生成了~BSTree()//析構函數，利用后序遍歷析構，從葉子節點開始析構，運用遞歸{Destroy(_root);_root = nullptr;}void Destroy(Node* root)//這里我們把Destroy單獨封裝，因為要寫遞歸{if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}BSTree(const BSTree<K>& bst)//拷貝構造{_root = Copy(bst._root);}Node* Copy(Node* root)//這里要從根節點開始復制，運用的是先序遍歷{if (root == nullptr){return nullptr;}Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}bool Insert(K key){if (_root == nullptr)//如果樹為空，則直接插入{_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur)//直到cur為空為止{if (cur->_key > key)//結點值大于插入值，則往左孩子方向走{parent = cur;cur = cur->_left;}else if (cur-> _key < key)//結點值小于插入值，則往右孩子方向走{parent = cur;cur = cur->_right;}else//結點值等于插入值，我們這里不支持插入相等值{return false;}}if (key < parent->_key)//cur到空后你并不知道插入值比父節點大還是小，判斷后再插入{parent->_left = new Node(key);}if (key > parent->_key){parent->_right = new Node(key);}return true;}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);}bool Find(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//開始刪除if (cur->_right == nullptr)//只有左子樹{if (cur == _root)//如果要刪除的為根節點，如果不寫，下面的parent就會使空，//空的引用會報錯{_root = cur->_left;}else{if (parent->_left == cur)//如果父節點的左孩子為要刪除的節點{parent->_left = cur->_left;//cur只有左子樹，把左子樹放在父節點的左子樹上}if (parent->_right == cur)//如果父節點的右孩子為要刪除的節點{parent->_right = cur->_left;//把cur左子樹放到父節點的右子樹上}}delete cur;}else if (cur->_left == nullptr)//只有右子樹{if (_root == cur){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}if (parent->_right == cur){parent->_right = cur->_right;}}delete cur;}else//左右子樹都有，將要刪除的節點與中序遍歷的前驅節點（中序遍歷前一個結點）//或后繼節點（中序遍歷的后一個節點）交換//中序遍歷的前驅節點即待刪除節點的左子樹的最大節點，也就是左子樹最右節點//中序遍歷的后繼節點即待刪除節點的右子樹的最小節點，也就是右子樹最左節點{Node* replace = cur->_right;Node* replaceParent = cur;while (replace->_left)//尋找右子樹的最左節點{replaceParent = replace;replace = replace->_left;}swap(replace->_key, cur->_key);if (replaceParent->_left == replace)//有兩種情況(通過replaceParent和replace有沒有移動來判斷)：有可能找到了最左節點replaceParent->_left = replace->_left;else//還有可能replace就沒有左節點，此時它為右子樹最小節點replaceParent->_right = replace->_right;delete replace;}return true;}}return false;}
private :Node* _root = nullptr;
};void test()
{int arr[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : arr){t.Insert(e);}t.InOrder();//cout << t.Find(3) << endl;//cout << t.Find(5) << endl;////左右都不為空//t.Erase(8);//t.InOrder();//t.Erase(3);//t.InOrder();////右為空//t.Erase(14);//t.InOrder();////左為空//t.Erase(6);//t.InOrder();//for (auto e : arr)//{//	t.Erase(e);//	t.InOrder();//}BSTree<int> t1(t);t1.InOrder();
}

test.cpp

#define _CRT_SECURE_NO_WARNINGS 1#include "BinarySelectTree.h"int main()
{test();return 0;
}

4、key 和 key / value（ map 和 set 的鋪墊 ）?

? 在二叉搜索樹中，我們都是以 key 作為樹排序的依據的，比如整型的插入，結點里存儲的整型就是它的鍵值，也就是我們這里所說的 key ，key 是二叉搜索樹排序的依據。

? key的應用場景，比如我們小區的門衛系統，如果車主住在小區，那么業主的汽車的信息就會存入門衛系統，每次只需要按照 key 來查找就可以了（當然小區系統存儲肯定用的是數據庫，但也可以是二叉搜索樹的應用，只不過存儲空間小，這樣存儲的數據都存到內存里了，容易弄丟）。

? 接著就是鍵值對 key / value，這個就是 map 的關鍵，上面說過，multimap 是支持等值存儲的，在 multimap 中，key 和 value 是綁定存儲的，比如我們在 multimap 中存儲了 3 這個整型，那么鍵值 key 就是 3 ，如果他只出現了一次，那么 value 就是 1 ，每多存儲一個 key ，value 就++，當然，這只是? multimap 的一個應用，value同樣可以存儲字符串等，這里只是告訴大家兩者是綁定的。

? 但是有一點大家要知道，不管是 map 和 set ，都只看key，而不去看value。

OK,到這里我們的二叉搜索樹就結束了，接下來我們將要面對的是高階數據結構，讓我們一起加油吧。