1. 問題描述

我們現在寫一個3D的Unity程序，我們現在設置了一個物體后，我們想旋轉使其改為我們想要的情況。但是我們如果rotation輸入了3個值后，我們發現現在旋轉的時候，rotation的值會突然跳轉變換到另一個值。這個時候我們修改例如x的值，y和z值也會隨著x值發生變化。我們在這種情況下難以通過不斷調整三個坐標軸的旋轉將我們的物體旋轉到我們想要的情況。

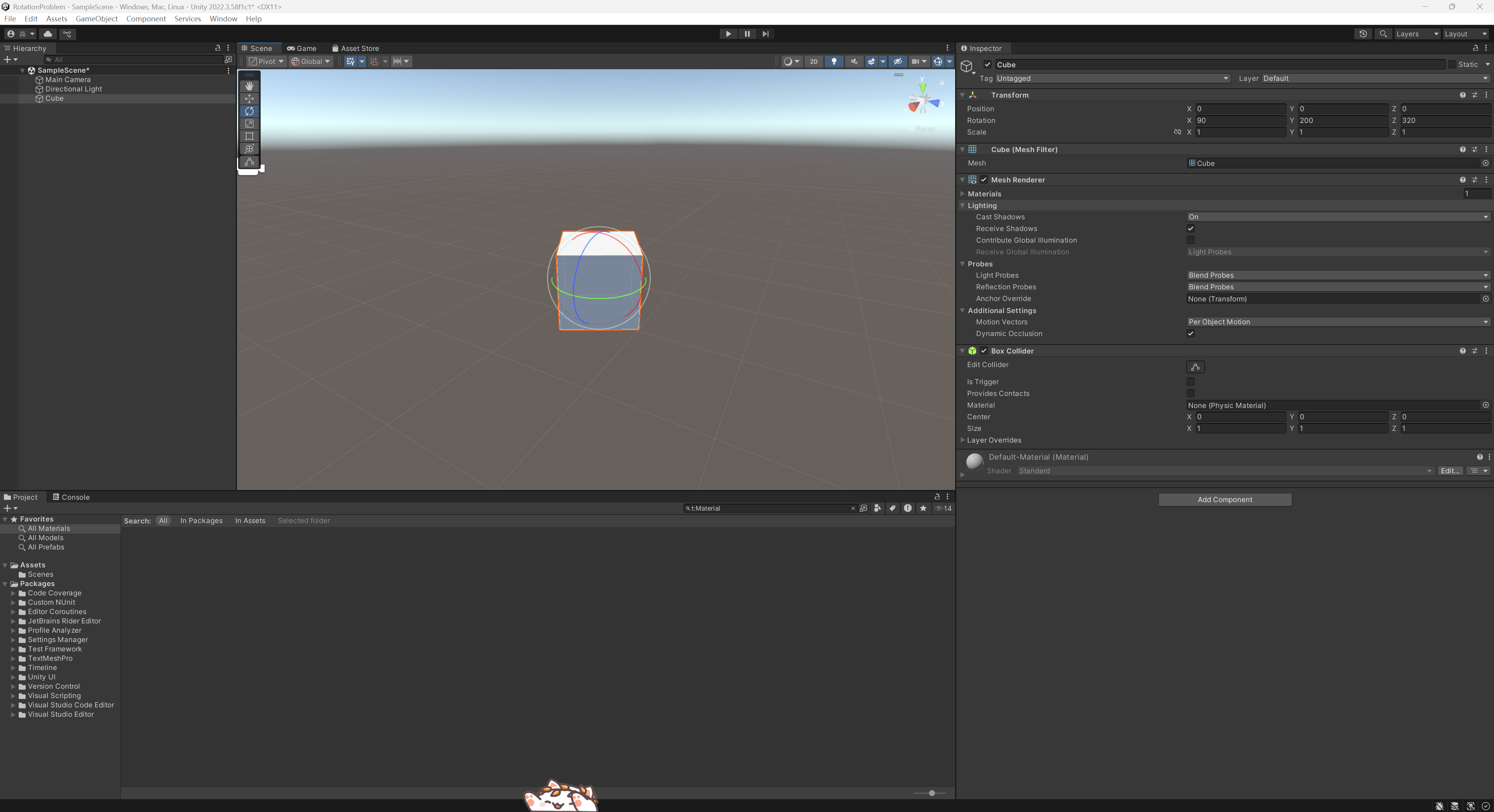
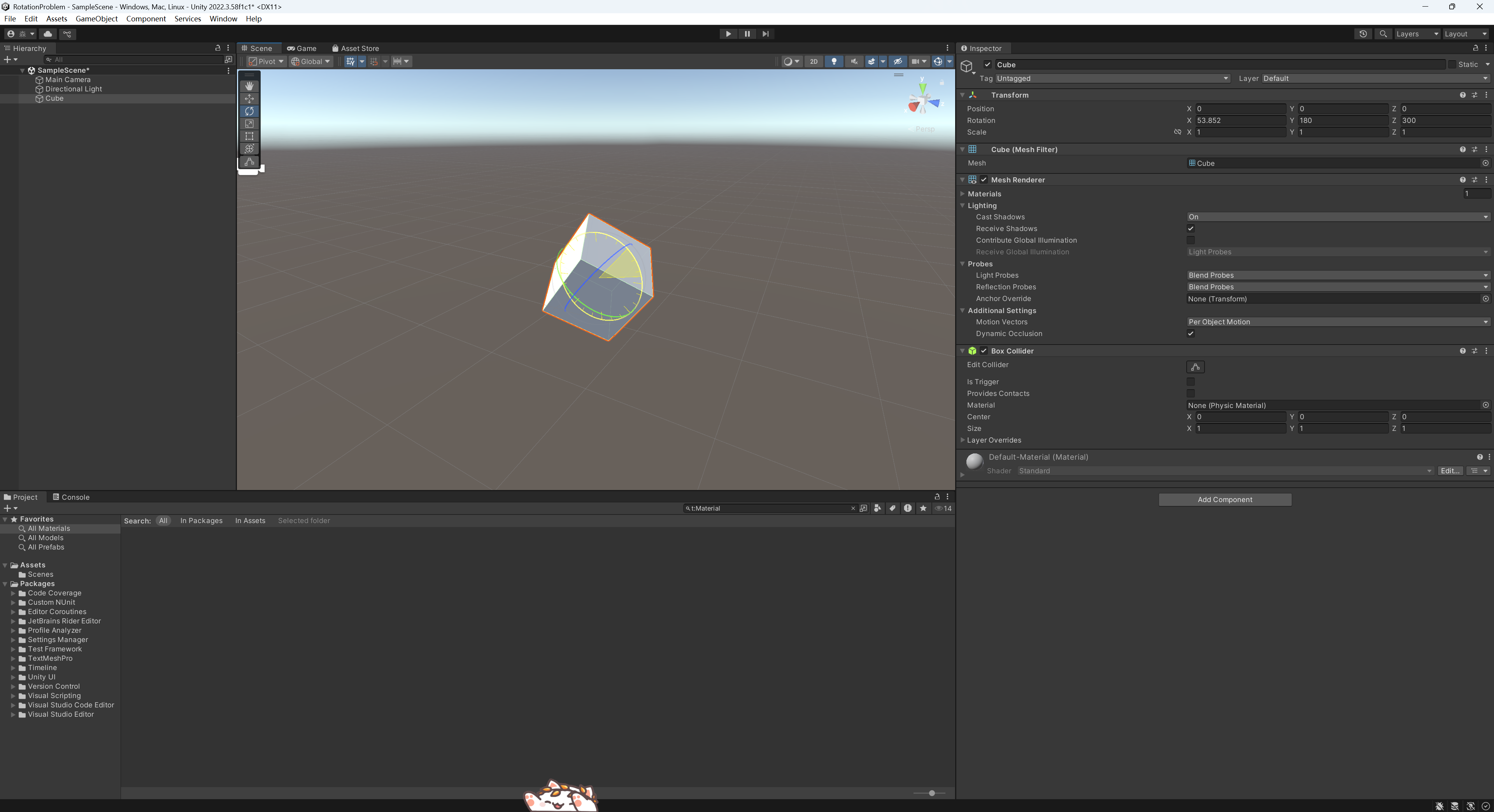
2. 問題原因

了解圖形學的話，我們知道旋轉（Rotation）是變換（Transformation）的一種，其底層計算使用矩陣來表示。
我們一般使用homogeneous co0ordinates（齊次坐標）來進行計算。
在三維空間中，繞z軸的旋轉可以看作是在所有z坐標相同的平面上進行的二維旋轉。
因此關于z軸旋轉的情況如下：

關于y軸和x軸旋轉的情況如下：

由于是矩陣計算，矩陣乘法有結合律但是沒法使用交換律。
因此當我們完成了旋轉之后，我們再次更改值，旋轉順序就被我們打亂了，因此矩陣的值會突然發生變化，此時我們再修改值，也不會是我們想象中的只變化一個軸的值，另外的值也會發生變化。

3. 解決方案

3.1通過多個父子關系從而控制旋轉（推薦）

在 Unity中，旋轉的順序是先繞 Z 軸旋轉，然后繞 X 軸旋轉，最后繞 Y 軸旋轉。也就是說，對于歐拉角 (30, 40, 50)，旋轉順序如下：

1. 先繞 Z 軸旋轉 50°。
2. 再繞 X 軸旋轉 30°。
3. 最后繞 Y 軸旋轉 40°。

因此我們可以分別使用三個父子關系從而分別控制不同的軸進行旋轉。
但是這里我們并不是Z軸在最外面作為父物體，而是Y軸在最外面作為父物體。
因為在 Unity 中使用父子關系來控制旋轉時，每個子物體的旋轉是相對于其父物體的局部坐標系進行的。在 Unity 中直接設置一個物體的歐拉角旋轉時，這個旋轉是相對于世界坐標軸的。
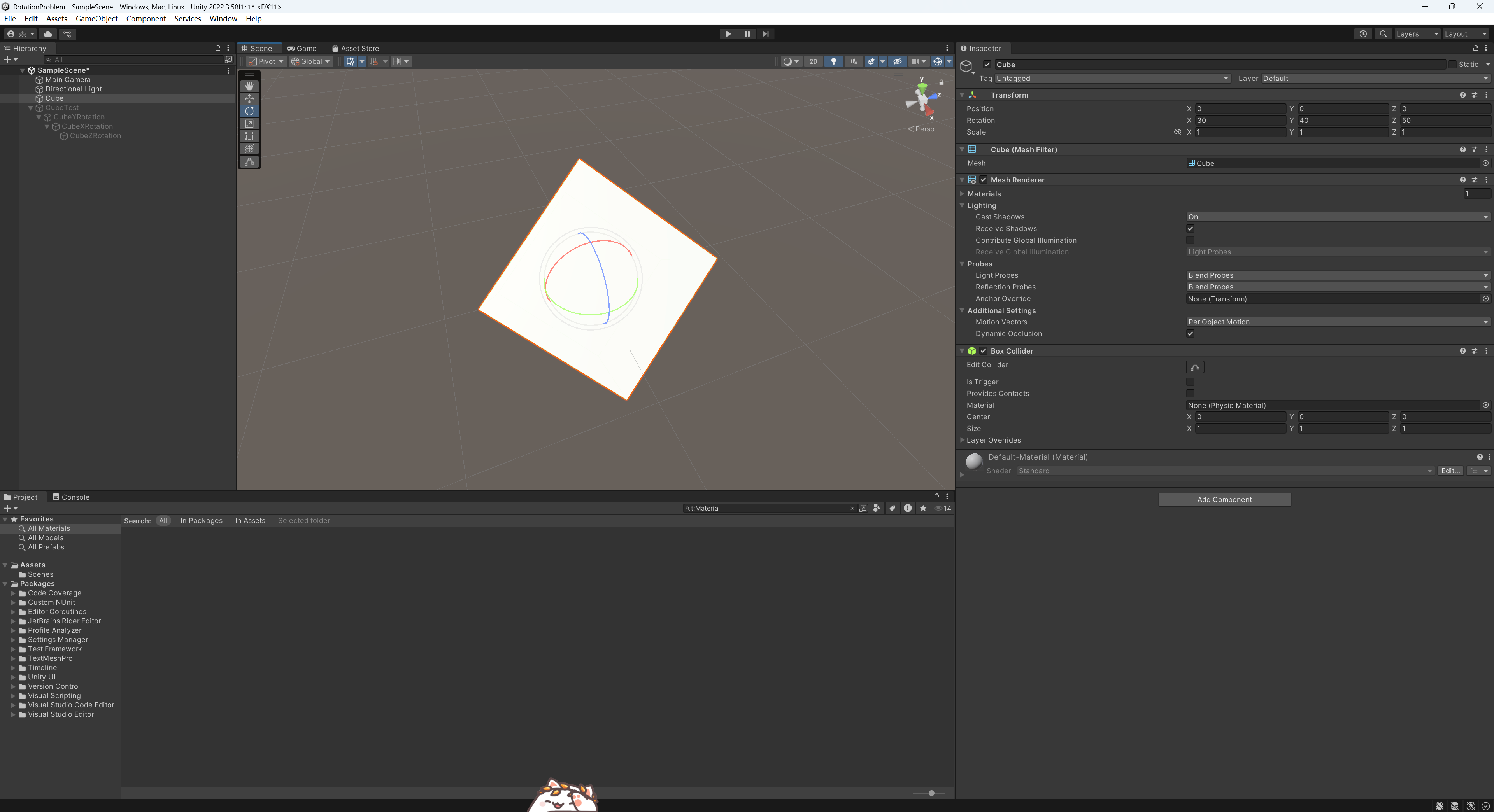
換句話說在Unity中根據自身坐標系旋轉的順序是Y-X-Z，根據世界坐標系旋轉的順序是Z-X-Y。所以這里正確的父子關系如圖所示，順序為Y-X-Z。

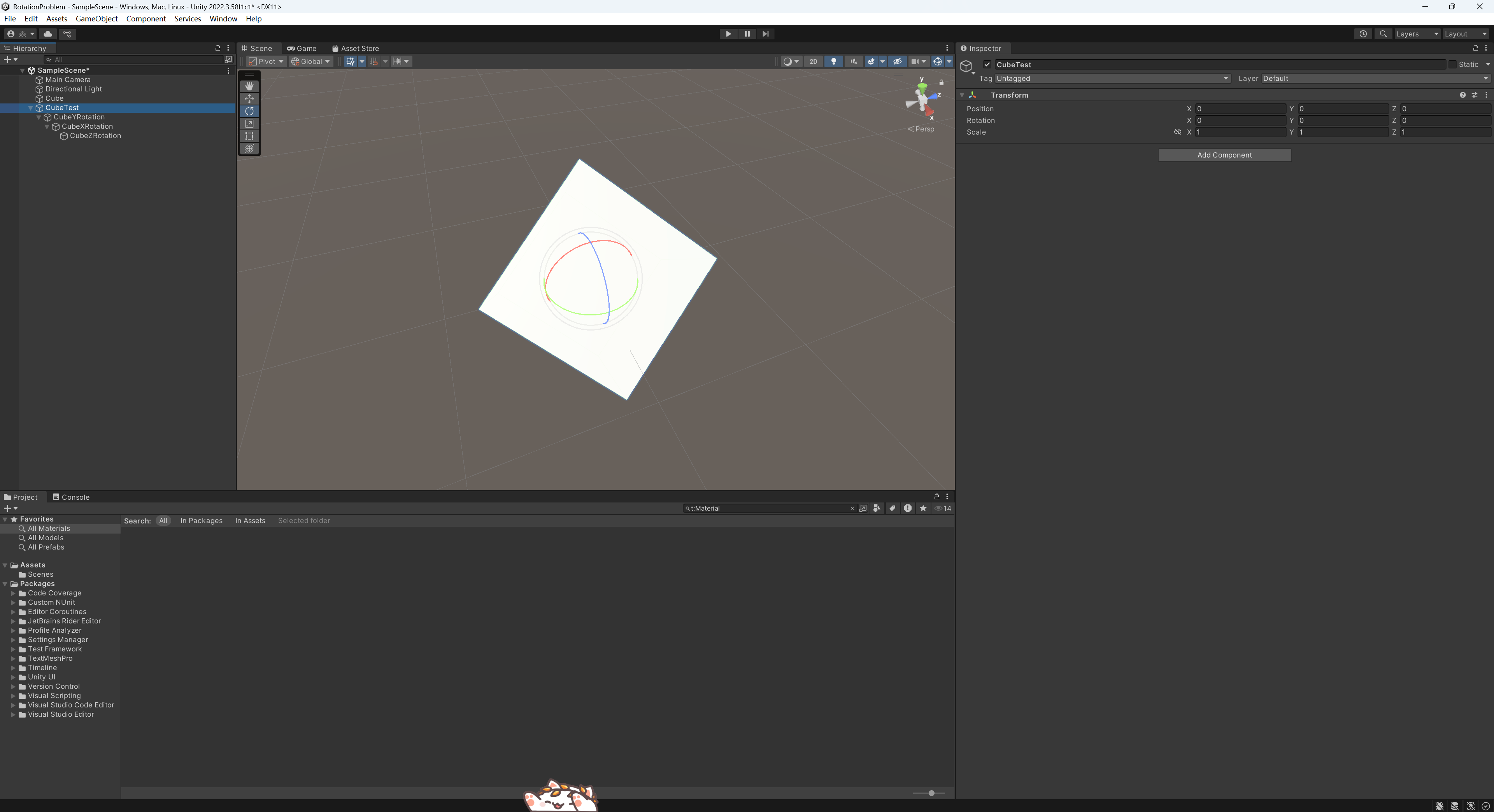
這里使用CubeYRotation控制Y軸的旋轉。

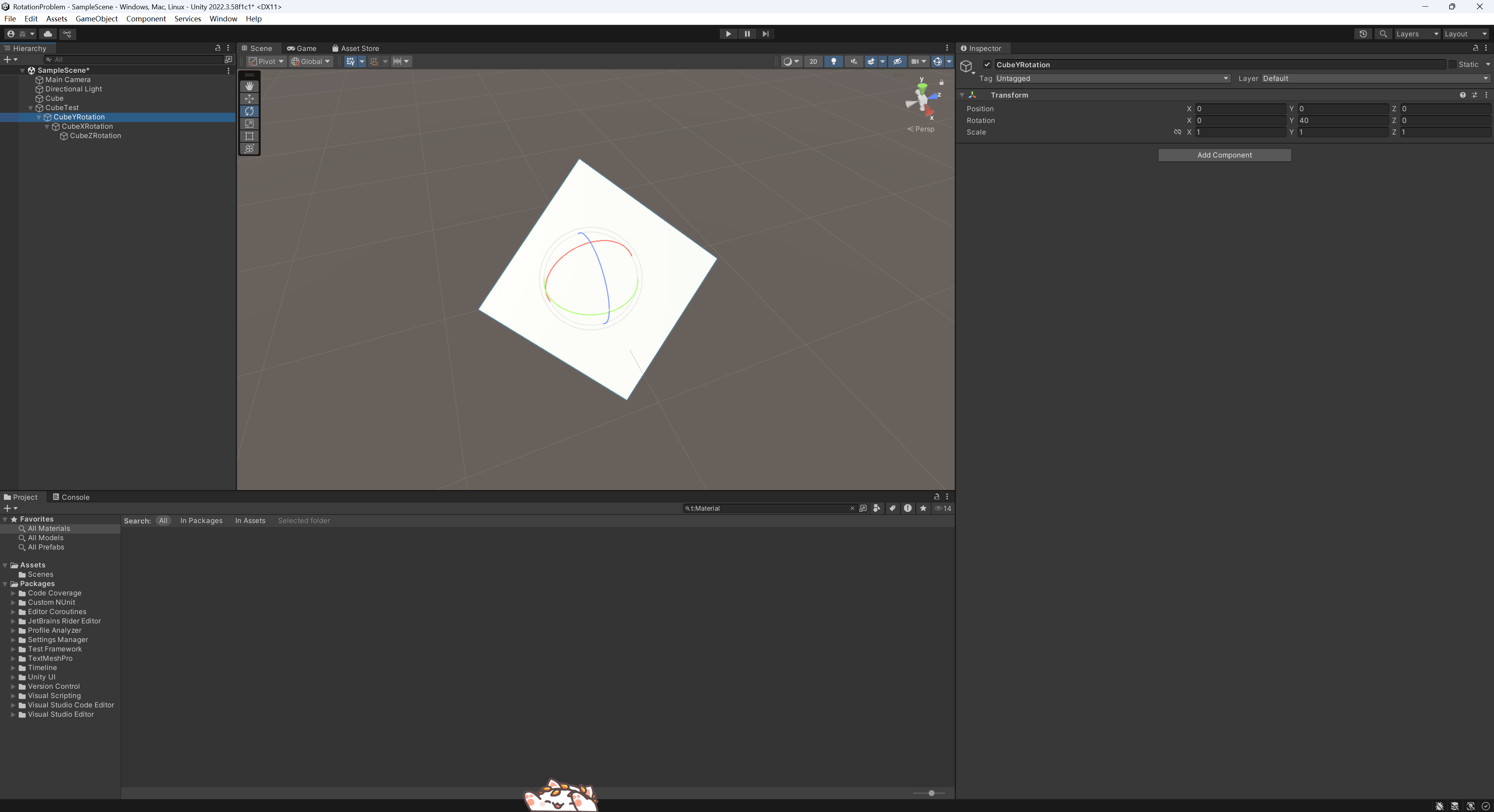
接著用其子物體CubeXRotation控制X軸的旋轉。

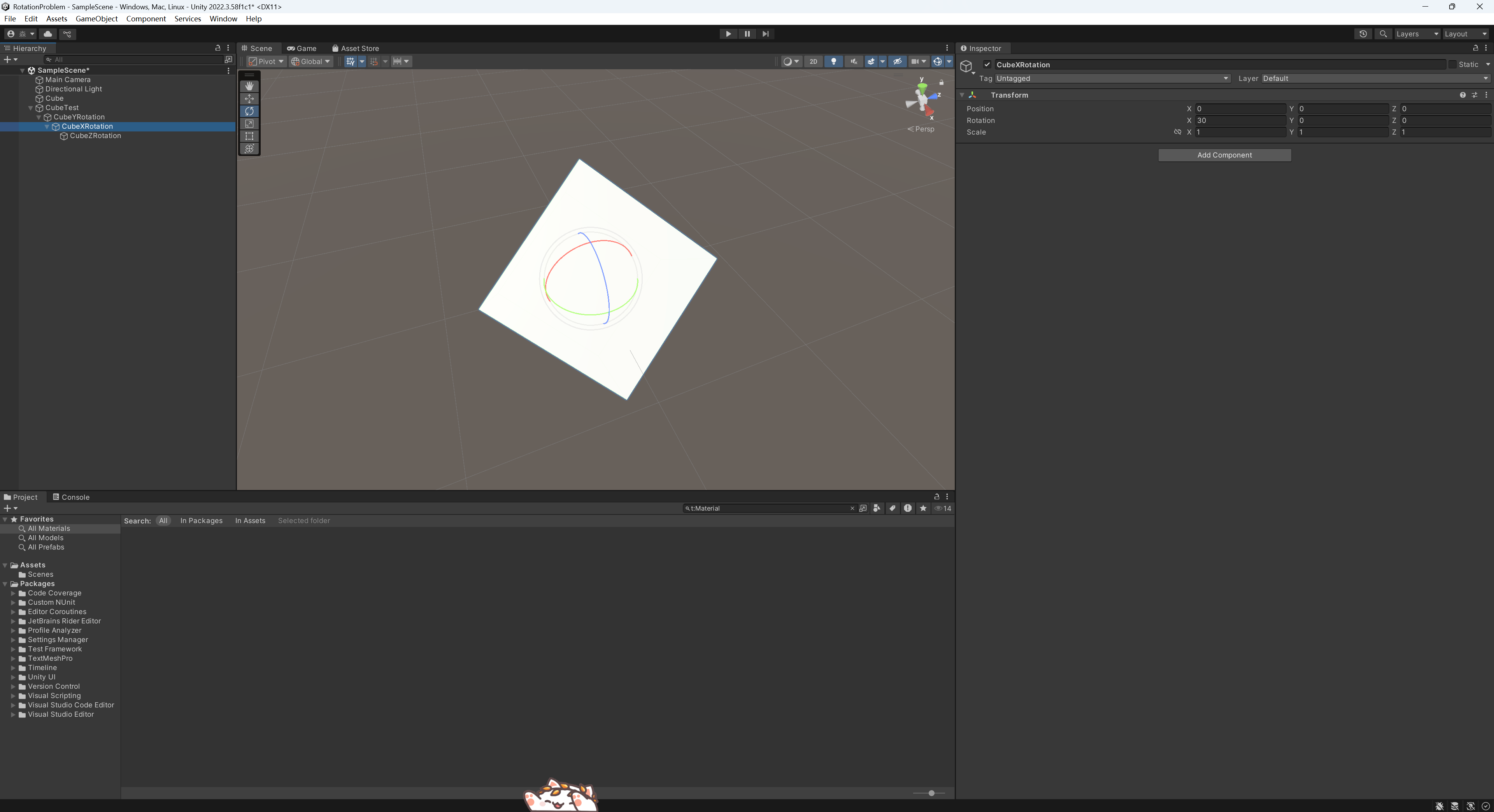
最后使用其子物體CubeZRotation控制Z軸的旋轉。

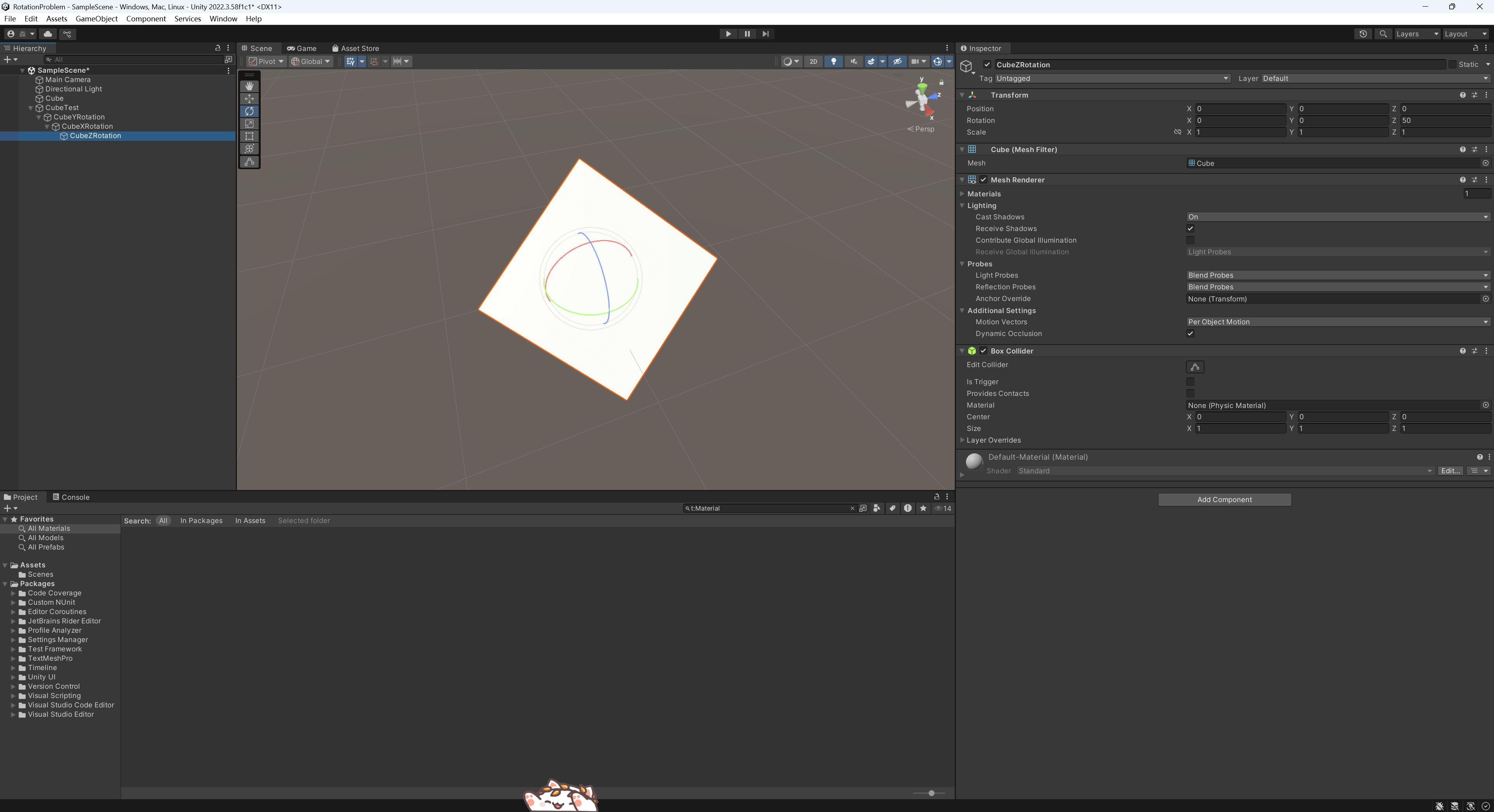
將其分別設置為和原來的Cube一樣的旋轉值，通過這樣的方式我們可以得到和原來的Cube一樣的效果，而且，這時候我們再分別旋轉這些對象的Rotation可以只修改一個軸的Rotation，不會產生一次旋轉多個值變化的情況。

這種方法易于控制，并且使用我們日常使用的歐拉角，所以方便理解，現實實踐的時候可以不按照這個順序進行控制，用這種父子關系控制旋轉即可。
我們在實際使用Unity中也可以多使用父子關系控制對象的變換（包含位置、旋轉、縮放），通過父子關系我們可以更好控制對象的位置關系和實際效果，還可以幫助我們更好管理對象的層級結構。
如圖所示，我將這個場景里的所有對象放在了一個大的父物體下，方便控制。

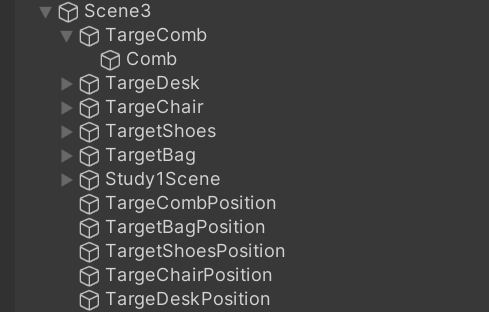
為了驗證前面我們的結論我們可以試驗下面的幾個代碼。
第一個代碼：

transform.Rotate(45, 45, 45);

第二個代碼：

transform.Rotate(0, 0, 45, Space.World);
transform.Rotate(45, 0, 0, Space.World);
transform.Rotate(0, 45, 0, Space.World);

第三個代碼：

transform.Rotate(0, 45, 0);
transform.Rotate(45, 0, 0);
transform.Rotate(0, 0, 45);

這三個代碼的效果一樣，也能說明在Unity中根據自身坐標系旋轉的順序是Y-X-Z，根據世界坐標系旋轉的順序是Z-X-Y。

3.2 使用四元數進行旋轉

如果我們學習Unity的教程，一般會告訴你旋轉Unity采取四元數來表示和計算旋轉，因為四元數不會像歐拉角一樣存在萬向鎖（萬向鎖是使用歐拉角表示旋轉時可能遇到的一個問題，即當旋轉到某些特定角度時，會失去一個維度的自由度，導致旋轉變得不穩定。）和表達方式多樣的問題（歐拉角有無數種表達方式，這可能導致在計算或存儲時出現混淆或錯誤）。
但是它并沒有歐拉角那樣易于理解，這里只稍微說下簡單的概念。
它是一種擴展了復數的概念，可以表示為一個實部和三個虛部的組合，通常表示為 $q=w+xi+yj+zk$，其中$w,x,y,z$是實數，而$i,j,k$是虛數單位。這里實部與旋轉的余弦值有關，虛部與旋轉軸的方向向量有關。
四元數可以表示為：$q=cos(\theta /2)+(u?i)sin(\theta /2)$其中，$\theta$是旋轉角度， $u$是旋轉軸的單位向量。

我們這里使用四元數進行旋轉，這是Unity比較推薦的方式。
我們先創建三個旋轉四元數，分別對應 X、Y、Z 軸的旋轉角度。然后將這三個四元數相乘，得到最終的旋轉四元數。將這里的最終四元數賦給物體的rotation從而完成旋轉。

Quaternion rotationX = Quaternion.Euler(30f, 0f, 0f);
Quaternion rotationY = Quaternion.Euler(0f, 40f, 0f);
Quaternion rotationZ = Quaternion.Euler(0f, 0f, 50f);
Quaternion finalRotation = rotationZ * rotationY * rotationX;transform.rotation = finalRotation;

這個方式相較于前者在Inspector里修改不夠直觀方便，因此更推薦前者。