題目鏈接
Leetcode快樂數
題目描述
?
如下圖:?
 ?
?
題目解析:
?1.雙指針法
算法核心思路
判斷快樂數的關鍵挑戰是如何檢測是否進入無限循環。這里使用了快慢指針法(Floyd 循環檢測算法),這是一種高效檢測循環的技巧:
- 慢指針:每次計算一次數字的平方和(走一步)
- 快指針:每次計算兩次數字的平方和(走兩步)
- 如果是快樂數:最終都會收斂到 1,此時快慢指針會相遇在 1
- 如果不是快樂數:快慢指針會在某個非 1 的數字處相遇(檢測到循環)

算法執行流程示例
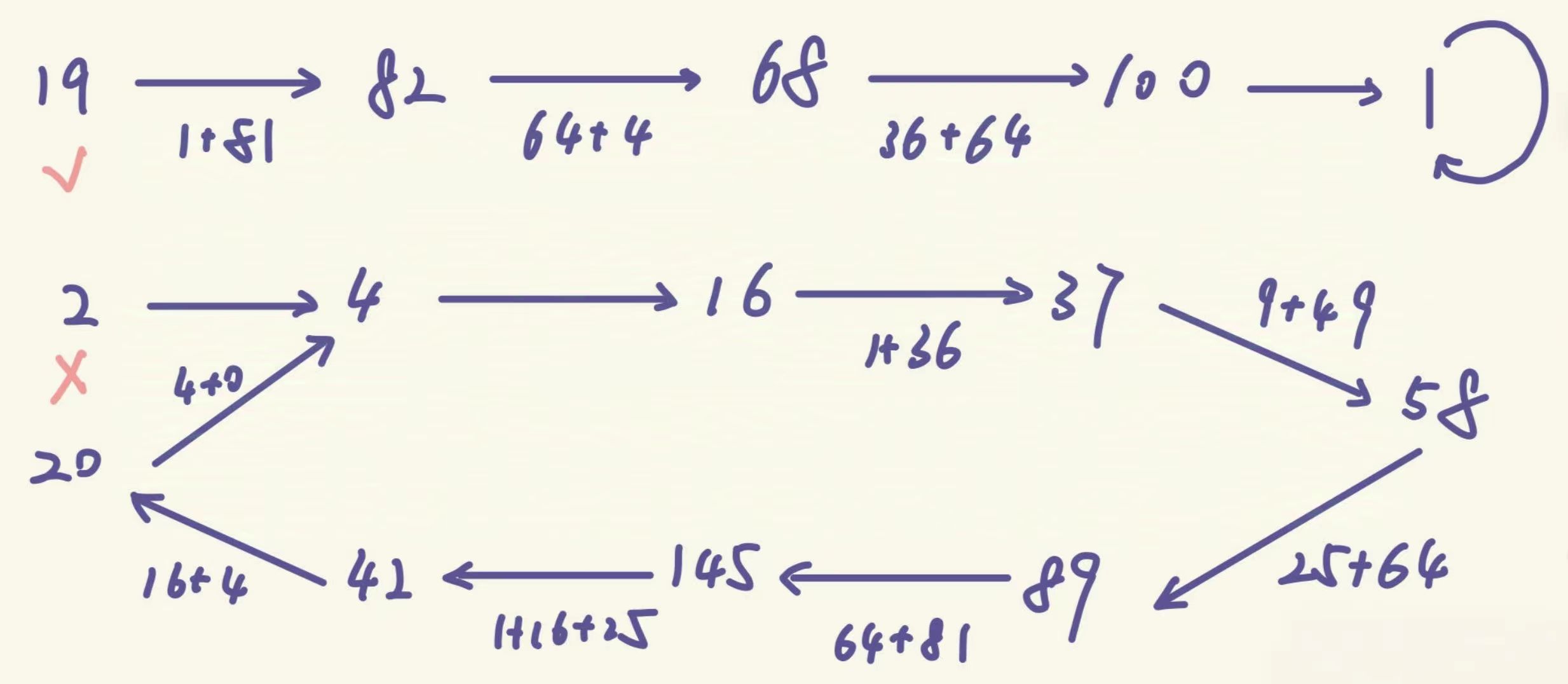
以非快樂數 11 為例,看看算法如何工作:
- 初始狀態:slow=11,fast=11
- 第一次循環:
- slow = Sum(11) = 12 + 12 = 2
- fast = Sum(Sum(11)) = Sum(2) = 4
- 此時 slow≠fast,繼續循環
- 第二次循環:
- slow = Sum(2) = 4
- fast = Sum(Sum(4)) = Sum(16) = 12 + 62 = 37
- 此時 slow≠fast,繼續循環
- 后續循環中,快慢指針會逐漸接近,最終在某個非 1 的數字相遇,此時返回 false
算法復雜度分析
-
時間復雜度:O(log n)
- 每次計算平方和時,數字的位數大約是 log??n
- 快慢指針相遇前最多執行 O (log n) 次操作
-
空間復雜度:O(1)
- 只使用了常數個額外變量,沒有使用額外的數據結構
?
2.哈希表法?
使用哈希表(Hash Set)求解快樂數問題是另一種直觀且容易理解的方法。其核心思路是記錄每次計算得到的平方和,如果某個平方和重復出現,說明進入了循環,該數不是快樂數;如果最終得到 1,則是快樂數。?
哈希表解法思路?
1.計算數字的各位平方和?
2. 檢查該平方和是否為 1:
?????若是 1,返回 true(是快樂數)
???? 若不是 1,檢查該平方和是否已在哈希表中:?
- 若已存在,說明進入循環,返回 false(不是快樂數)
- 若不存在,將其加入哈希表,繼續計算下一個平方和?
?完整代碼:
代碼解析
-
getSum 函數:與之前的 Sum 函數功能相同,計算一個數的各位數字平方和。
-
isHappy 函數:
- 使用
unordered_set<int> seen存儲已經出現過的數字 - 循環計算平方和,直到結果為 1 或檢測到循環:
- 若 n=1,返回 true(找到快樂數)
- 若 n 已在哈希表中,返回 false(檢測到循環)
- 否則將 n 加入哈希表,繼續計算下一個平方和
- 使用
?
執行流程示例(以 19 為例)
- 初始 n=19,哈希表為空
- 19 不在哈希表中,加入哈希表,計算下一個值:12+92=82
- 82 不在哈希表中,加入哈希表,計算下一個值:82+22=68
- 68 不在哈希表中,加入哈希表,計算下一個值:62+82=100
- 100 不在哈希表中,加入哈希表,計算下一個值:12+02+02=1
- 此時 n=1,返回 true(19 是快樂數)
復雜度分析
-
時間復雜度:O(log n)
- 每次計算平方和處理 log??n 位數字
- 最多處理 O (log n) 個不同的數字(因為平方和的增長有上限)
-
空間復雜度:O(log n)
- 最壞情況下,哈希表需要存儲 O (log n) 個不同的數字
?
















)


