一、p129-JZ21使奇數位于偶數前面（不考慮相對位置）（hoare快排雙指針）

調整數組順序使奇數位于偶數前面(二)_牛客題霸_牛客網

? ? ? ? ?如果不考慮相對位置的話，那么我們可以模仿hoare快排，使用雙指針的思想，一個指針在前向后找偶數，一個指針在后，向前找奇數，然后再交換就行 時間復雜度是n?

class Solution {public:vector<int> reOrderArrayTwo(vector<int>& nums) {//用雙指針int n = nums.size();if (n == 0) return{};int left = 0, right = n - 1;//左邊找偶數，右邊找奇數 然后交換while (left < right) {while (left < right && nums[left] & 1) ++left;while (left < right && (nums[right] & 1) == 0) --right;if (left < right) swap(nums[left], nums[right]);}return nums;}
};

二、p129-JZ21使奇數位于偶數前面（考慮相對位置）（插入排序）

調整數組順序使奇數位于偶數前面(一)_牛客題霸_牛客網

因為要考慮相對位置，所以我們就要借鑒一下插入排序的思想?

class Solution {public:vector<int> reOrderArray(vector<int>& nums) {//奇數位于偶數前面，并且還要保證相對位置不變//那就得用到插入排序的思想了！ //從前往后 看到奇數我就想辦法往前挪//1 3 5 6 7int n = nums.size();int k = 0;for (int i = 0; i < n; ++i)if (nums[i] &1) { //從左向右，每次遇到的，都是最前面的奇數，一定將來要被放在k下標處int temp = nums[i]; //先將當前奇數保存起來int j = i;while (j >  k) { //將該奇數之前的內容(偶數序列)，整體后移一個位置nums[j] = nums[j - 1];--j;}//將奇數保存在它將來改在的位置，因為我們是從左往右放的，沒有跨越奇數，所以一定是相對位置不變的nums[k++] =temp; }return nums;}
};

??擴展：如果面試官問你如果想要把題目改成將負數放在非負數前面，或者將可以被3整除的放在不能被3整除的數的前面，這個時候我們可以通過傳入仿函數來設計一套通用的解法，然后只需要在判斷的邏輯那里調用仿函數可以。這樣可以實現解耦成兩部分：一是判斷數字應該在數組的前半部分還是后半部分的標準，而是拆分數組的操作。

三、p249-JZ51數組中的逆序對（歸并排序）

數組中的逆序對_牛客題霸_牛客網

? ? 該題能夠使用歸并排序，本質是利用了待合并有序數組的單調性，我們在題目中需要去找到區間前的數和區間后的數存在某種大小關系的時候，我們就可以用分治思想中的歸并排序在兩段待排序的升序區間中根據單調性去找我們想要的結果。

升序的做法： 以后面區間為基點，找前面區間有多少數字比我大

class Solution {
public:
//升序 以l2為基準 找前面有多少數字比我大const int MOD=1e9+7;int InversePairs(vector<int>& nums) {int n=nums.size();vector<int> temp(n);return mergesort(nums,0,n-1,temp);}int mergesort(vector<int>& nums,int begin,int end,vector<int>& temp){if(begin>=end) return 0;int mid=(begin+end)>>1;int ret=mergesort(nums,begin,mid,temp)+mergesort(nums,mid+1,end,temp);int cur1=begin,cur2=mid+1,i=begin;while(cur1<=mid&&cur2<=end)if(nums[cur1]<=nums[cur2]) temp[i++]=nums[cur1++];else{ret+=mid-cur1+1;ret%=MOD;temp[i++]=nums[cur2++];}while(cur1<=mid) temp[i++]=nums[cur1++];while(cur2<=end) temp[i++]=nums[cur2++];//開始還原for(i=begin;i<=end;++i) nums[i]=temp[i];return ret;}
};

降序的做法： 以前面區間為基點，找后面區間有多少數字比我小

class Solution {
public:
//降序 以l1為基準 找后面有多少數字比我小const int MOD=1e9+7;int InversePairs(vector<int>& nums) {int n=nums.size();vector<int> temp(n);return mergesort(nums,0,n-1,temp);}int mergesort(vector<int>& nums,int begin,int end,vector<int>& temp){if(begin>=end) return 0;int mid=(begin+end)>>1;int ret=mergesort(nums,begin,mid,temp)+mergesort(nums,mid+1,end,temp);int cur1=begin,cur2=mid+1,i=begin;while(cur1<=mid&&cur2<=end)if(nums[cur1]<=nums[cur2]) temp[i++]=nums[cur2++];else{ret+=end-cur2+1;ret%=MOD;temp[i++]=nums[cur1++];}while(cur1<=mid) temp[i++]=nums[cur1++];while(cur2<=end) temp[i++]=nums[cur2++];//開始還原for(i=begin;i<=end;++i) nums[i]=temp[i];return ret;}
};

?四、p209-JZ40最小的k個數（快速選擇排序）

最小的K個數_牛客題霸_牛客網

方法1：建大堆 一個個和堆頂比較，最后剩下的k個數要找的（適合處理海量數據）

#include <queue>
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {int n=input.size();if(k==0||n==0||k>n) return {};//搞一個大根堆  然后讓前k個進去  然后再一個個排除 最后剩下的就是最小的k個數priority_queue<int> q;for(int i=0;i<k;++i) q.push(input[i]);//前k個丟進去//然后開始排除for(int i=k;i<n;++i) if(input[i]<q.top()){q.pop();q.push(input[i]);}//插入到數組中返回vector<int> ret(k);for(int i=0;i<k;++i){ret[i]=q.top();q.pop();}return ret;}
};

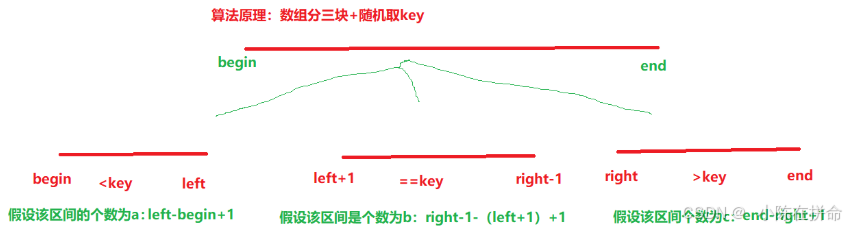
方法2：快速選擇排序算法（適合單次查找且可以修改原數組的情況下）

#include <cstdlib>
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));//時間種子qsort(nums,0,nums.size()-1,k);return {nums.begin(),nums.begin()+k};}void qsort(vector<int>& nums,int begin,int end,int k){if(begin>=end) return;//要按照數組分三塊的思想int key=nums[rand()%(end-begin+1)+begin];int left=begin-1,right=end+1,cur=begin;while(cur<right)if(nums[cur]<key) swap(nums[cur++],nums[++left]);else if(nums[cur]>key) swap(nums[--right],nums[cur]);else ++cur;//根據區間大小進行選擇int a=left-begin+1,b=(right-1)-(left+1)+1;if(k<a) qsort(nums,begin,left,k);//說明在左邊區間里 繼續排序else if(k<=a+b) return;else qsort(nums,right,end,k-a-b);//說明在第三塊區間里}
};

五、p214-JZ41數據流中的中位數（優先級隊列）

數據流中的中位數_牛客題霸_牛客網

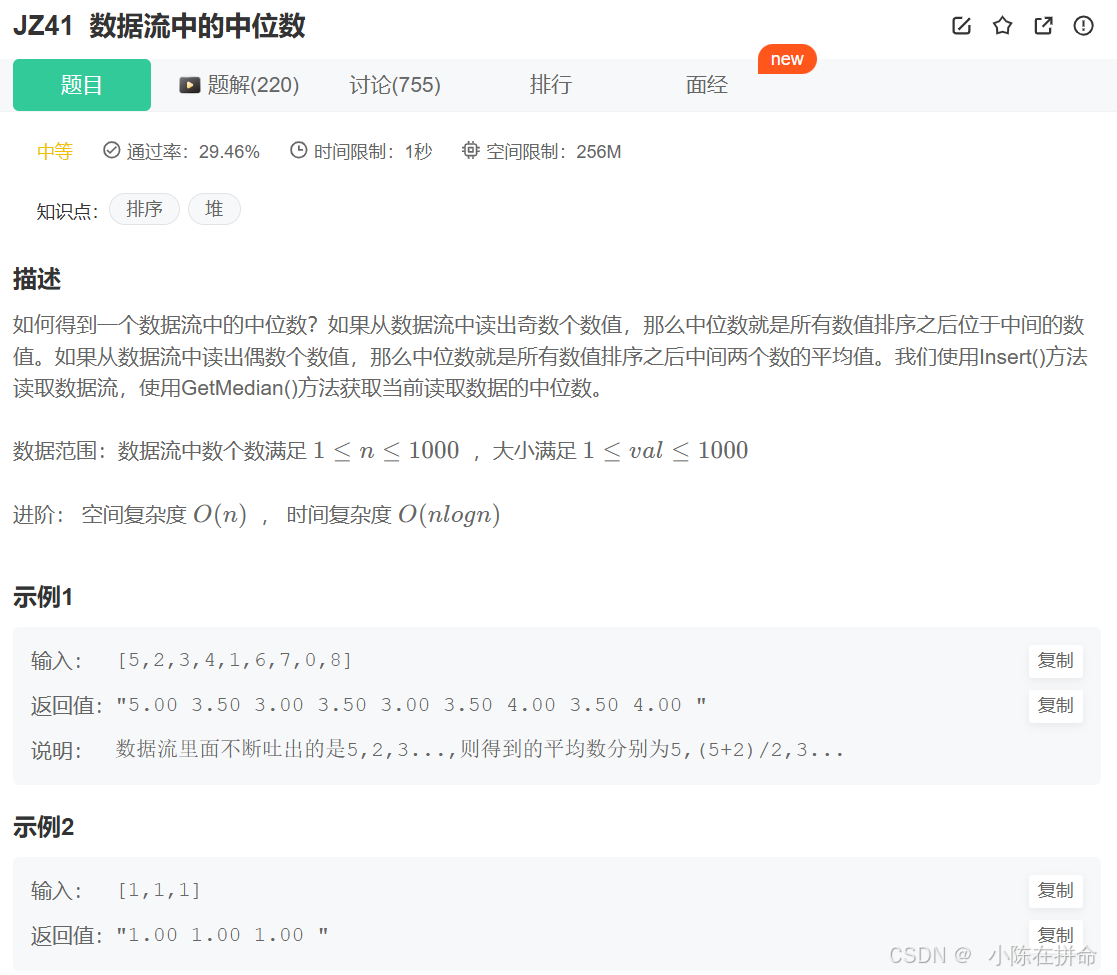
策略：優先級隊列大小堆維護中位數 ? add(logN) ?find(1)

設計思路：

1、建立left為大根堆，right為小根堆

2、我們的add控制始終保持left的數量要么和right相等，要么比right多一個，為了能夠滿足在O（1）的復雜度內完成找到中位數的任務，我們希望當left多一個的時候，left堆頂的元素就是中位數，而當left和right相等的時候，中位數就是兩個堆的堆頂元素的平均值。

3、為了達到這個目的，我們在時刻控制left和right的數量的同時，一定要保證left里面的元素是小于等于right里面的元素的，所以add要分兩種情況去討論：

情況1：當兩個堆的元素個數相等的時候

? ? （1）如果left為空，或者是add的元素比left的堆頂元素小，那么就讓該元素直接進left

? ? （2）如果add的元素比left的堆頂元素大，那么他也有可能會比right的元素大，所以我們必須要將這個元素丟到right中，但是直接丟就會破壞規則，所以我們要先將add的元素丟到right中進行調整，然后再將right的堆頂元素丟到left中去，保持left和right的數量關系。 （注意，這里的先后順序很重要，我們不能先將right的堆頂元素丟到left中，然后再將add丟到right中進行調整，因為我們只是知道這個數比left的堆頂元素大，但是他是比right的堆頂元素大還是小我們不得而知，必須要通過他自己的向下調整去選出來）

情況2：當left的元素比right多一個的時候

? （1）如果add的元素比left的堆頂元素大，這個時候無腦進右邊就行了。

? ?（2）如果add的元素比left的堆頂元素小，這個時候我們也得把add的元素丟到left中，然后為了保持數量關系，將調整過后的left的堆頂元素移到right中即可。

細節處理：

1、我們在比較的時候始終實用left的元素進行比較，因為左邊不為空的時候右邊也可能為空，所以我們如果不用left去比較而是用right去比較，那么還需要多考慮一種邊界情況。

2、雖然我們add的都是int類型，但是當兩個堆的元素個數相同的時候，我們去取兩個堆頂元素取平均值的，而平均值是有可能會出現小數的，所以如果我們還用int的話可能會造成小數點丟失，所以我們在/2的時候變成/2.0,這樣結果就會被強轉成double；

class Solution {
public:void Insert(int num) {//如果為空 直接插入左邊//如果兩邊一樣多,  若<=left 直接插左邊 若>right 就先插入右邊 然后再移堆頂int m=left.size(),n=right.size();if(m==n)if(left.empty()||num<=left.top()) left.push(num);else{//num>left>left.topright.push(num);left.push(right.top());right.pop();} //如果左邊比右邊多  else{//m==n+1if(num>left.top()) right.push(num);else{//num<=left.topleft.push(num);right.push(left.top());left.pop();}}}double GetMedian() { //如果左邊比右邊多 就返回左邊     如果相等就返回中間值if(left.size()>right.size()) return left.top();else return (left.top()+right.top())/2.0;}
private://需要有一個大根堆(在前面) 一個小根堆(在后面)priority_queue<int> left;//大根堆priority_queue<int,vector<int>,greater<int>> right;///右邊是小根堆
};

六、p227-JZ45把數組排成最小的數（重寫排序/冒泡排序）

把數組排成最小的數_牛客題霸_牛客網

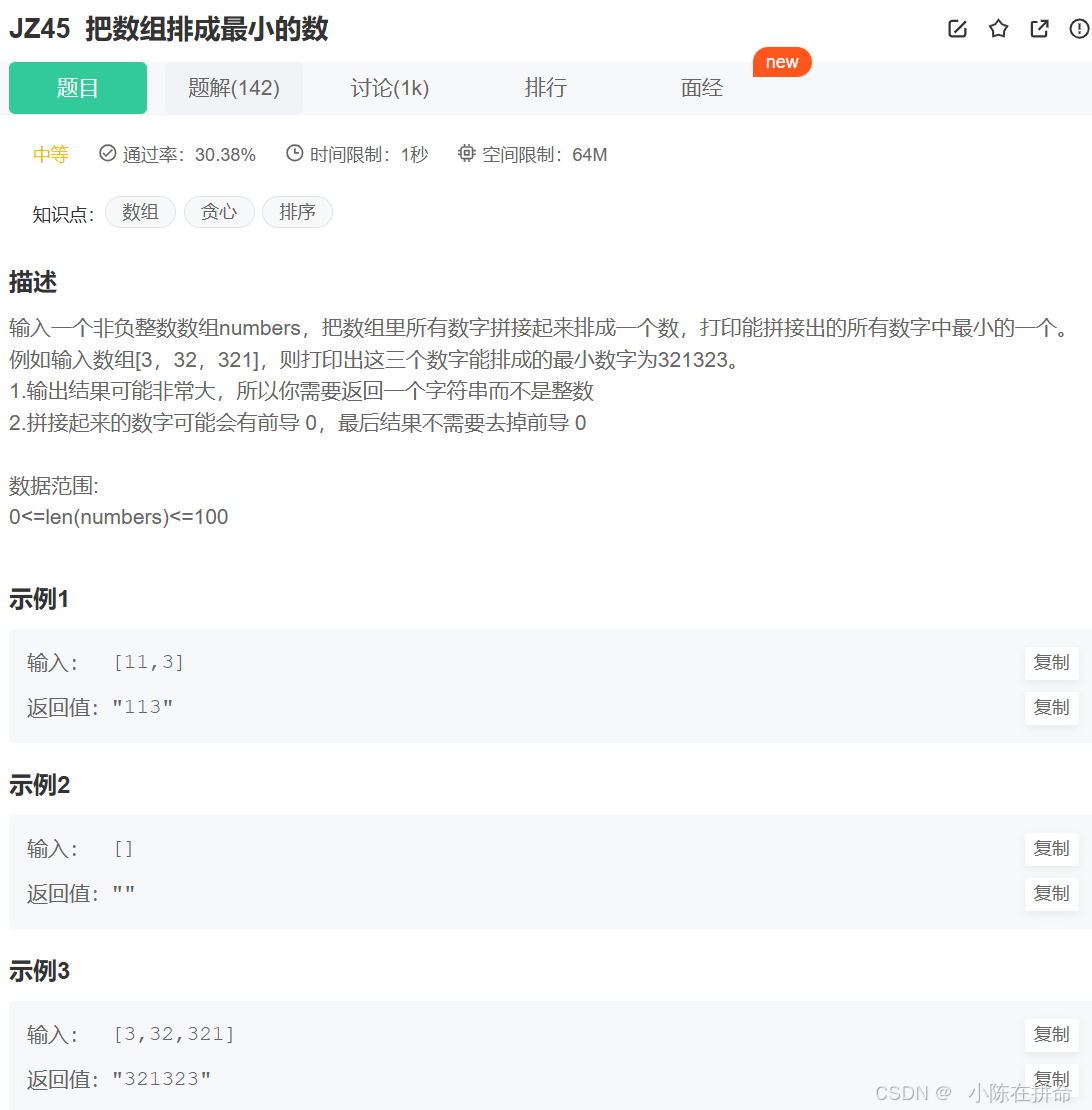
方法一：重載比較的排序（推薦使用）

具體做法：

• step 1：優先判斷空數組的特殊情況。
• step 2：將數組中的數字元素轉換成字符串類型。
• step 3：重載排序比較為字符串類型的x + y < y + x，然后進行排序。
• step 4：將排序結果再按照字符串拼接成一個整體。

class Solution {
public:string PrintMinNumber(vector<int>& nums) {int n=nums.size();if(n==0) return"";vector<string> strs;strs.reserve(n);for(auto&num:nums) strs.emplace_back(to_string(num));sort(strs.begin(),strs.end(),[&strs](const string&s1,const string&s2){return s1+s2<s2+s1;});string ret;for(auto&s:strs) ret+=s;return ret;}
};

方法二：冒泡排序（擴展思路）

class Solution {
public:string PrintMinNumber(vector<int> numbers) {string res = "";//空數組的情況if(numbers.size() == 0)return res;vector<string> nums;//將數字轉成字符for(int i = 0; i < numbers.size(); i++)nums.push_back(to_string(numbers[i]));//冒泡排序for(int i = 0; i < nums.size() - 1; i++){for(int j = 0; j < nums.size() - i - 1; j++){string s1 = nums[j] + nums[j + 1];string s2 = nums[j + 1] + nums[j];//比較拼接的大小交換位置if(s1 > s2) swap(nums[j], nums[j + 1]);}}//字符串疊加for(int i = 0; i < nums.size(); i++)res += nums[i];return res;}
};

七、p280-JZ57和為S的兩個數字（雙指針+單調性）

和為S的兩個數字_牛客題霸_牛客網

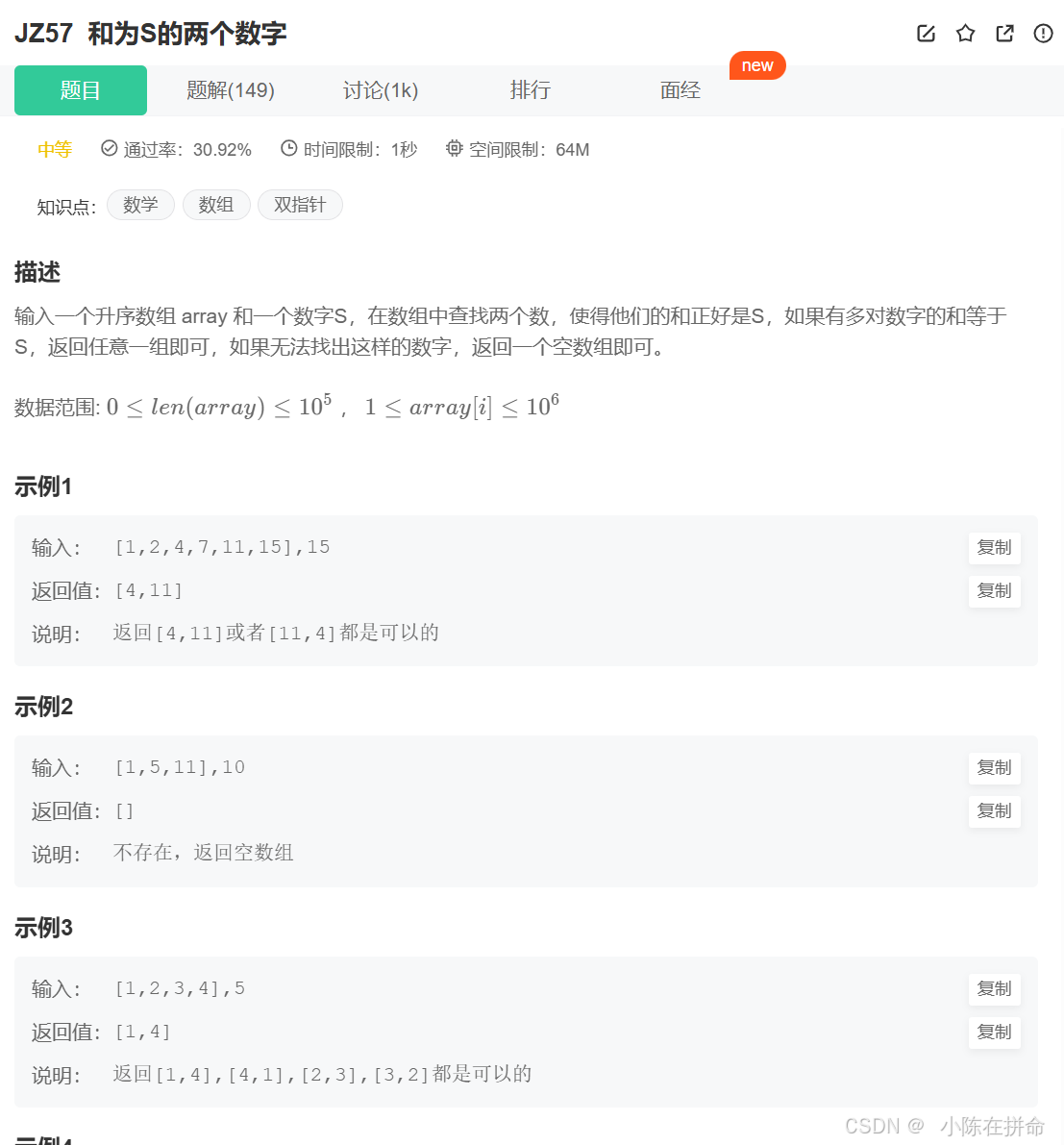
思路：

我們能想到最直觀的解法，可能就是兩層遍歷，將數組所有的二元組合枚舉一遍，看看是否是和為目標值，但是這樣太費時間了，既然加法這么復雜，我們是不是可以嘗試一下減法：對于數組中出現的一個數a，如果目標值減去a的值已經出現過了，那這不就是我們要找的一對元組嗎？這種時候，快速找到已經出現過的某個值，可以考慮使用哈希表快速檢驗某個元素是否出現過這一功能。

具體做法：

• step 1：構建一個哈希表，其中key值為遍歷數組過程中出現過的值
• step 2：遍歷數組每個元素，如果目標值減去該元素的結果在哈希表中存在，說明我們先前遍歷的時候它出現過，根據保存的值，就可以得到結果。
• step 3：如果相減后的結果沒有在哈希表中，說明先前遍歷的元素中沒有它對應的另一個值，那我們將它加入哈希表，等待后續它匹配的那個值出現即可。

class Solution {
public:vector<int> FindNumbersWithSum(vector<int> nums,int sum) {unordered_set<int> hash; //在哈希表中查找sum-array[i]for(auto&e:nums){int temp=sum-e;if(hash.find(temp)==hash.end()) hash.insert(e);else return {temp,e};}return {};}
};

思路：

這道題目還有一個條件是數組是升序序列，在方法一中沒有用到。這個條件有什么用？既然數組是有序的，那我們肯定知道和找到一定程度就不找了，我們為什么要從最小的兩個數開始相加呢？我們可以用二分法的思路，從中間開始找。

使用雙指針指向數組第一個元素和最后一個元素，然后雙指針對撞移動，如果兩個指針下的和正好等于目標值sum，那我們肯定找到了，如果和小于sum，說明我們需要找到更大的，那只能增加左邊的元素，如果和大于sum，說明我們需要找更小的，只能減小右邊的元素。

具體做法：

• step 1：準備左右雙指針分別指向數組首尾元素。
• step 2：如果兩個指針下的和正好等于目標值sum，則找到了所求的兩個元素。
• step 3：如果兩個指針下的和大于目標值sum，右指針左移；如果兩個指針下的和小于目標值sum，左指針右移。
• step 4：當兩指針對撞時，還沒有找到，就是數組沒有。

class Solution {
public:vector<int> FindNumbersWithSum(vector<int> nums,int sum) {//雙指針int left=0,right=nums.size()-1;while(left<right){int x=nums[left]+nums[right];if(x<sum) ++left;else if(x==sum) return{nums[left],nums[right]};else --right;}return {};}
};

八、擴展p282-JZ57 和為S的連續正數序列（滑動窗口）

?和為S的連續正數序列_牛客題霸_牛客網

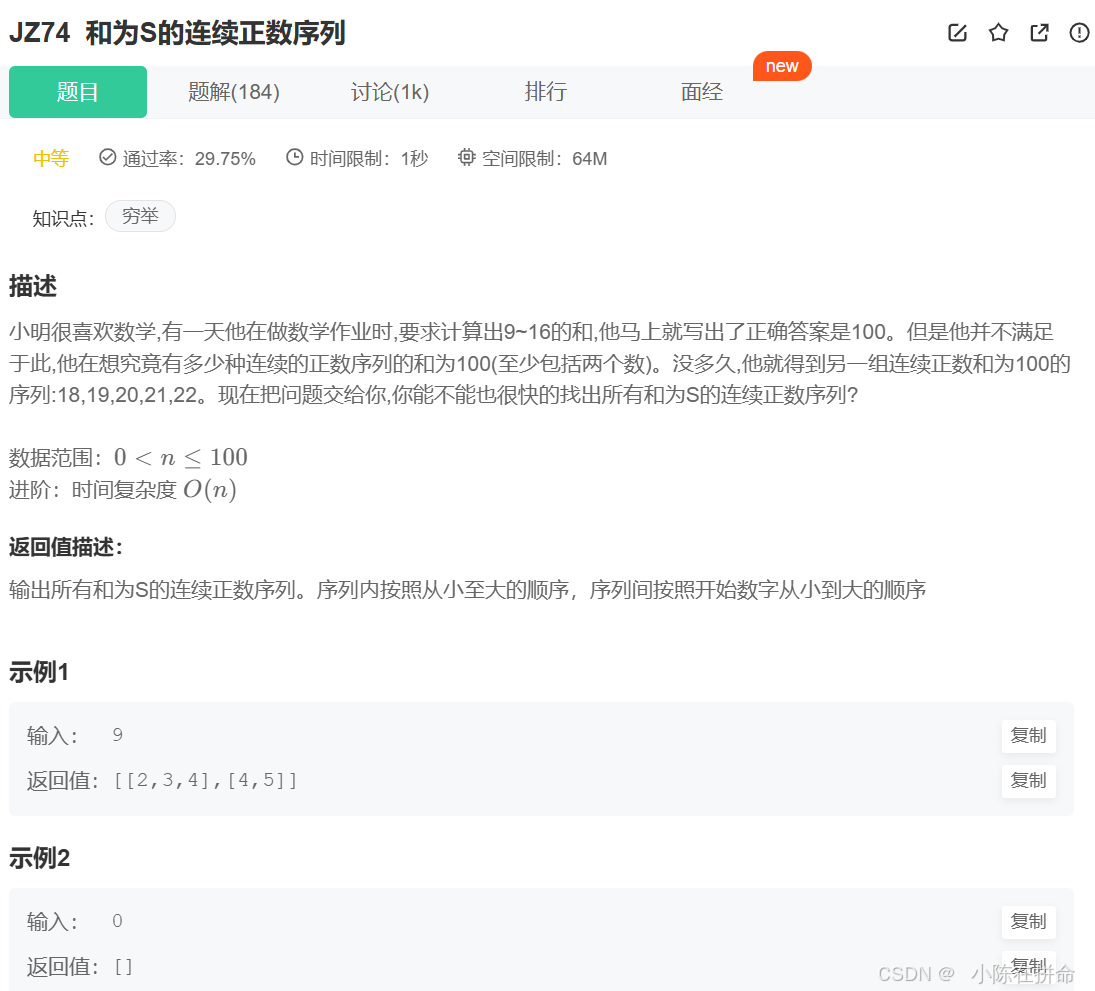
思路：

從某一個數字開始的連續序列和等于目標數如果有，只能有一個，于是我們可以用這個性質來使區間滑動。

兩個指針l、r指向區間首和區間尾，公式(l+r)?(r?l+1)/2(l+r)?(r?l+1)/2計算區間內部的序列和，如果這個和剛好等于目標數，說明以該區間首開始的序列找到了，記錄下區間內的序列，同時以左邊開始的起點就沒有序列了，于是左區間收縮；如果區間和大于目標數，說明該區間過長需要收縮，只能收縮左邊；如果該區間和小于目標數，說明該區間過短需要擴大，只能向右擴大，移動區間尾。

具體做法：

• step 1：從區間[1,2][1,2]開始找連續子序列。
• step 2：每次用公式計算區間內的和，若是等于目標數，則記錄下該區間的所有數字，為一種序列，同時左區間指針向右。
• step 3：若是區間內的序列和小于目標數，只能右區間擴展，若是區間內的序列和大于目標數，只能左區間收縮。

class Solution {
public:vector<vector<int>> FindContinuousSequence(int n) {//滑動窗口if(n<3) return {};vector<vector<int>> ret;//結果集vector<int> path;//存儲結果for(int left=1,right=2,total=3;left<right;total-=left,++left){while(total<n){++right;total+=right;}if(total==n){for(int i=left;i<=right;++i)  path.emplace_back(i);ret.emplace_back(path);path.clear();//清空}}return ret;}
};