本節主要講的是模型訓練時的算法設計
數據預處理:
關于數據預處理,我們有常用的3個符號,數據矩陣X,假設其尺寸是,N是數據樣本的數量,D是數據的維度
均值減法(Mean subtraction):
是預處理最常用的形式,它對數據中每個獨立特征減去其該獨立特征在所有樣本中的平均值
對于圖片來說,更常見的時對所有像素都減去所有像素值的平均值,也可以在3個顏色通道上分別操作
歸一化(Normalization):
指將數據的所有維度都歸一化,使其數值范圍都近似相等
這個操作的意義在于當不同維度的輸入特征具有不同的數值范圍(或計量單位)且差異較大時,可以避免傳播時部分特征相關的權重的梯度過大
在圖像處理中,由于像素的數值范圍幾乎是一致的,所以額外進行這個預處理步驟就顯得沒有那么必要
歸一化的兩種方法:
第一種方法:
對數據做0中心化處理,然后對每個維度都除以其維度對應的標準差
即
其中S為X的標準差
第二種方法:
對每個維度都做歸一化,使得每個維度的最大值和最小值是1和-1
即
PCA與白化(Whitening):
我們可以對協方差矩陣進行SVD(奇異值分解),并利用奇異值分解來減小數據矩陣的size
這里先來復習一下SVD
SVD的描述如下:
奇異值:
設是秩為r的
?的矩陣,則
是對稱矩陣且可以正交對角化,則
的特征值
,設對應的特征向量為
, 則規定奇異值
,且
奇異值分解:
矩陣A同上,那么存在一個矩陣,其中D的對角元素是A的前r個奇異值,滿足排序
,且存在一個
?的正交矩陣U和一個
?的正交矩陣V,使得
其中
?是U的第i個列向量,當m>n時,多余的u自行補充單位向量,使U滿足正交矩陣
和上面提到的意義一致,構成V的第i個列向量
PCA過程:
原理:
設表示以
為樣本觀測值的是隨機變量,如果能找到
,使得
的值達到最大,就表明了這m個變量的最大差異,當然需要規定
,否則Var可以是無窮大
這個解是m維空間的一個單位向量,代表一個方向,稱之為主成分方向
一般來說代表原來m個變量的主成分不止一個,但不同主成分信息之間不能相互包含,即兩個主成分的協方差應為0
即:
設表示第i個主成分
則要使
達到最大,又要有
與
垂直,且使
達到最大,以此類推,至多可以得到m個主成分
步驟:
1.先對數據進行0中心化處理,然后計算協方差矩陣R(這里也是相關系數矩陣),假設size為
R的第(i,j)個元素是第i個維度和第j個維度的協方差,所以可以知道,這個矩陣是一個方陣,且是對角矩陣,且對角線上的元素,比如第(i,i)個元素,恰好是第i維特征的方差。且該矩陣是半正定矩陣
2.計算出R的特征值,以及對應的標準正交化特征向量
,其中
則得到m個主成分,第i個主成分為
,其中
已經被歸一化了
3.計算前j個主成分的累計貢獻率:
取定貢獻率一個閾值,比如75%,進而解得j,從而確定保留j個主成分
4.最后我們保留j個主成分代替之前的m個X進行分析即可,也就是把維度m降低到了j
實際計算中,我們常用SVD代替步驟2的特征分解(計算效率更高),也就是先對數據矩陣進行標準化,然后直接對數據矩陣D進行SVD分解(跳過計算協方差矩陣這一步),然后用SVD的V里的替代上文的
,
就取
的
,假設最后保留j個主成分,其對應的向量為
,則降維后的矩陣變成
優點:
通常使用PCA降維后的數據訓練神經網絡的性能會更好,同時節省時間和儲存器空間
白化:
目的是為了讓數據具有以下特性:
1.均值為0,數據分布的中心在原點
2.單位協方差,所有維度的方差為1
3.無相關性,不同維度之間完全獨立,協方差為0
步驟:
1.中心化,減去均值
2.計算協方差矩陣
3.對協方差矩陣進行特征值分解
4.對每個維度除以其特征值的平方根,在除的時候,為了防止分母為0,需要添加一個小常量
PCA與白化通常不用于卷積神經網絡
預處理重要規則:
對于訓練集/驗證集/測試集,我們在中心化的時候,只采用集合內有的樣本所產生的統計特征量進行預處理,比如,對訓練集進行預處理的時候,只用訓練集的均值/方差;對驗證集、測試集同理
權重初始化:
小隨機數初始化:
由于數據經過了恰當的歸一化處理,可以假設所有權重數值大約一半為正數,一半為負數,則其期望應為0,但又不能全為0,因為神經元之間是不對稱的,所以,我們可以將權重初始化為小的數值,隨機且不相等,通常的隨機是從基于0均值和標準差為1的高斯分布中生成隨機數。但不是小數值就一定會得到好的結果,因為這樣會導致反向傳播時出現非常小的梯度,從而很大程度地減小反向傳播中的梯度信號
使用?來校準方差
上述的做法存在一個問題,隨著輸入數據量的增大,隨機初始化神經元的輸出數據分布中的方差也在增大,因此,我們需要將其除以輸入數據量的平方根,來調整其方位,使其輸出的方差歸一化到1
證明過程如下:
第三個等號到第四個等號用到了
所以,如果想要s和x有一樣的方差,就需要滿足,又我們之前是由標準差為1的高斯分布隨機取得w,所以
,所以我們只要令
即可
稀疏初始化(Sparse initialization):
將所有權重矩陣設為0,但為了打破對稱性,每個神經元都要與下一層固定數目(經典連接數目是10個)的神經元隨機連接(權重由小的高斯分布生成)
偏置的初始化:
通常將偏置初始化為0,這是因為隨機數權重矩陣已經打破了對稱性,對于ReLU非線性激活函數,有人喜歡用0.01這樣的小數值常量作為所有偏置的初始值,認為這樣做能夠使所有的ReLU單元一開始就激活
批量歸一化(Batch Normalization):
核心思想是在網絡的每一層(尤其是全連接層/卷積層之后,激活函數之前),對輸入數據進行標準化處理,使其在訓練過程中保持相對穩定的分布,從而緩解梯度消失/爆炸,提高對初始化和學習率的魯棒性
步驟:
假設我們有一個mini_batch的數據輸入,size為m,對于每個神經元的輸入,我們都計算mini_batch的均值以及方差,并利用這個均值與方差對輸入進行標準化
正則化(Regularization):
控制神經網絡過擬合的方法之一
L2正則化:
對每個權重w,我們都向Loss中添加一項,系數為
?是因為這樣子梯度的系數就為1了,L2正則化的直觀理解是它對大數值的權重向量進行嚴厲的乘法,傾向于更加分散的權重向量,使網絡更傾向于使用所有輸入特征,而不是嚴重依賴于輸入特征中的某些小部分特征
使用L2正則化意味著所有的權重梯度都會有一個以的線性下降的方向成分
L1正則化:
對每個w我們向Loss加入,L1正則化會讓權重向量在最優化的過程中變得稀疏(非常接近0),也就是說使用L1正則化后,神經元更傾向于使用輸入數據中最重要特征所構成的稀疏子集,同時對噪聲的輸入不敏感。
一般來說L2正則化的效果要優于L1正則化
最大范氏約束(Max norm constraints)
另一種形式的正則化,給每個神經元的權重向量的量級設定上限,并使用投影梯度下降來確保這一約束,即,其中c為常數,一般為3或4,這種正則化有一個好處,在學習率設置過高的時候,網絡中也不會出現數值爆炸,因為參數更新始終被限制
隨機失活(Dropout):
非常簡單且有效的正則化方法
實現方法:在訓練時,讓神經元以p(超參數)的概率被激活或者設置為0(失活)
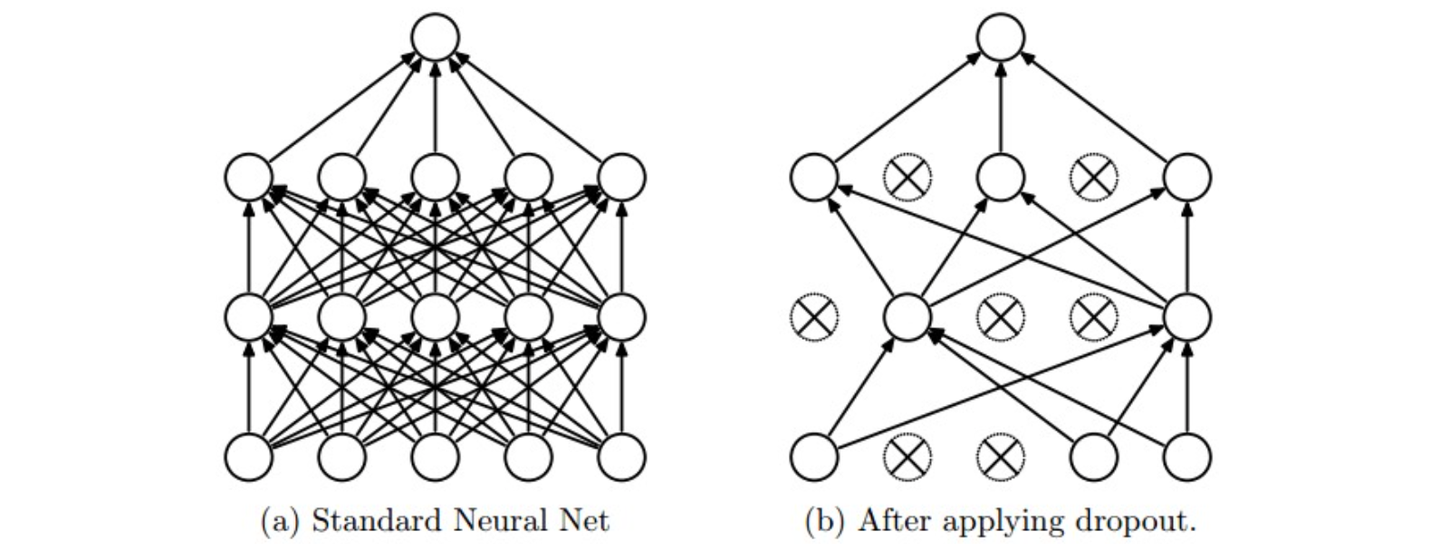
在訓練過程中,可以認為是對完整的神經網絡中抽樣出一些子集,每次基于輸入數據只更新子網絡的參數(但子網絡并不是相互獨立的,它們都共享參數)
在測試過程中,不再使用隨機失活,而是使用整個神經網絡進行預測,可以理解為對數量巨大的子網絡做了模型集成(model ensemble),從而計算出一個平均的預測
前向傳播中的噪聲:
Dropout屬于網絡在前向傳播中具有隨機行為的方法,則會對真實分布產生一定的噪聲,可以通過分析法、數值法將噪聲邊緣化
分析法:
由于Dropout只在訓練時進行隨機失活,導致每個神經元對其接受的輸入x的期望是px。則在預測的時候,不再隨機失活,為了保證神經元能夠復現之前訓練的環境,來保證其預測的正確性,需要將其接受的每個輸入x乘上一個系數p,從而保證同樣的預測期望輸出
數值法:
抽樣出很多的子網絡,隨機選擇不同的子網絡進行前向傳播,最后對他們的預測取平均值
損失函數:
屬性分類:
之前講到的損失公式的前提,都是假設每個樣本只有一個正確的標簽,但如果每個樣本都可以有或沒有多個標簽,且標簽之間互不排斥呢?
這種情況下,我們需要為每個屬性創立一個獨立的二分類的分類器,并都對其采用一個Loss函數,最后將這多個Loss函數求和
或者,我們可以對每種屬性訓練一種獨立的邏輯回歸分類器



顧客管理、供應商管理、用戶管理)


 流媒體解決方案)



CA1區域(vCA1)的混合調諧細胞(mixed-tuning cells)對NLP中的深層語義分析的積極影響和啟示)

)


: 陰影(shadowMap,PCF,PCSS))


![[STM32][HAL]stm32wbxx 超聲波測距模塊實現(HY-SRF05)](http://pic.xiahunao.cn/[STM32][HAL]stm32wbxx 超聲波測距模塊實現(HY-SRF05))
