上篇文章我們詳細介紹了堆和樹的基本概念以及它們之間的關系，還要知道一般實現堆的方式是使

用順序結構的數組進行存儲數據及實現。下來我們看看利用順序結構的數組如何實現對的內容:

1.堆的實現

關于堆的實現，也是三個文件，頭文件，實現文件和測試文件。下面我們逐一進行講解:

1.1 頭文件(Heap.h)

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//堆的結構
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;     //有效數據個數int capacity; //空間大小
}HP;//交換函數
void Swap(int* x, int* y);
//向上調整函數
void AdjustUp(HPDataType* arr, int child);
//向下調整函數
void AdjustDown(HPDataType* arr, int parent, int n);//初始化函數
void HPInit(HP* php);
//銷毀函數
void HPDestroy(HP* php);
//打印函數
void HPPrint(HP* php);//插入函數
void HPPush(HP* php, HPDataType x);
//刪除函數
void HPPop(HP* php);
//取堆頂數據
HPDataType HPTop(HP* php);// 判空函數
bool HPEmpty(HP* php);

以下從 頭文件作用、各部分代碼解析、整體功能梳理 角度，詳細介紹這個堆實現的頭文件：

1. 頭文件基礎作用

?#pragma once??是編譯器指令，保證頭文件 只被編譯一次，避免重復包含導致的符號沖突）。

引入的標準庫：

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

- ?stdio.h?：用于輸入輸出（如 ?HPPrint??可能用到 ?printf??打印堆內容 ）。

- ?stdlib.h?：提供內存分配（?malloc?/?free??）、數值轉換等函數，堆的動態擴容會用到。

- ?assert.h?：提供 ?assert??斷言，用于調試時檢查關鍵條件（如指針非空）。

- ?stdbool.h?：引入 ?bool??類型（?true?/?false??），讓代碼語義更清晰。

2. 堆的結構定義（?struct Heap?）

typedef int HPDataType;
typedef struct Heap
{HPDataType* arr; ? ?// 存儲堆數據的動態數組int size; ? ? ? ? ? // 堆中有效元素個數（當前堆的大小）int capacity; ? ? ? // 數組總容量（空間大小，避免頻繁擴容）
}HP;

- ?HPDataType?：用 ?typedef??把 ?int??重命名為 ?HPDataType?，方便后續修改堆存儲的數據類型

（如改成 ?float?/自定義結構體，只需改這里 ）。

- ?arr?：動態數組，底層用數組模擬堆結構（完全二叉樹按層序存儲特性，可通過下標快速找父子

節點 ）。

- ?size?：記錄當前堆中有多少個元素，決定堆的有效范圍。

- ?capacity?：記錄數組總共能存多少元素，?size??超過 ?capacity??時需要擴容。

3. 函數聲明解析（堆的核心操作）

//交換函數
void Swap(int* x, int* y);
//向上調整函數
void AdjustUp(HPDataType* arr, int child);
//向下調整函數
void AdjustDown(HPDataType* arr, int parent, int n);//初始化函數
void HPInit(HP* php);
//銷毀函數
void HPDestroy(HP* php);
//打印函數
void HPPrint(HP* php);//插入函數
void HPPush(HP* php, HPDataType x);
//刪除函數
void HPPop(HP* php);
//取堆頂數據
HPDataType HPTop(HP* php);// 判空函數
bool HPEmpty(HP* php);

頭文件里聲明的函數，覆蓋了堆的 初始化、銷毀、增刪查、調整 等功能，是堆的核心接口：

關于這些函數的實現, 我們在下一個實現文件中進行詳細解釋

?
4. 頭文件的整體作用

這個頭文件是堆的 “接口規范”：

- 對 調用者（其他 ?.c??文件）：只需包含頭文件，就能用堆的功能，不用關心底層實現。

- 對 實現者（寫堆邏輯的 ?.c??文件）：要按頭文件的函數聲明，去實現具體功能（如 ?HPInit??怎么

初始化、?HPPush??怎么擴容+調整 ）。

簡單說，頭文件像 “說明書”，定義了堆能用哪些功能、怎么用；實際的邏輯（函數體）寫在對應的

?.c??文件里，實現 “接口和實現分離”，讓代碼更清晰、易維護。

1.2 實現文件(Heap.c)

1. 堆初始化函數---HPInit函數

void HPInit(HP* php) 
{php->arr = NULL;php->size = php->capacity = 0;
}

功能：把堆的結構體成員置為初始狀態。

步驟：

1.??php->arr = NULL?：讓存儲堆數據的動態數組指針指向空，表明還沒分配內存。

2.??php->size = 0?：標記堆里當前沒有有效元素。

3.??php->capacity = 0?：標記數組容量為 0（還沒分配空間 ）。

復雜度：

- 時間復雜度：?O(1)??。直接賦值操作，和堆規模無關。

- 空間復雜度：?O(1)??。沒額外分配大內存，只是改幾個變量值。

聯系：是堆使用的“第一步”，后續?HPPush 等操作前，得先初始化堆結構體，讓指針、容

量、大小有合法狀態。

2. 堆的銷毀函數---HPDestroy函數

void HPDestroy(HP* php) 
{if (php->arr) {?free(php->arr);?php->arr = NULL;?}php->size = php->capacity = 0;
}

功能：釋放堆占用的動態內存，防止內存泄漏，把堆恢復到“初始空狀態”。

步驟：

1.?檢查 ?php->arr??是否非空（非空才需要釋放 ）。

2.?用 ?free(php->arr)??釋放動態數組內存，再把 ?php->arr??置 ?NULL?，避免野指針。

3.?把 ?size??和 ?capacity??置為 0，讓堆結構體回到初始化類似狀態。

復雜度：

- 時間復雜度：?O(1)??。就幾個判斷和賦值，釋放內存是常數時間）。

- 空間復雜度：?O(1)??。主要是釋放已有內存，沒新增大內存占用。

聯系：堆不用了就調用它，和 HPInit 呼應，一個負責“開”，一個負責“關”，保證內存合理管

理。

3. 堆打印函數---HPPrint函數

void HPPrint(HP* php) 
{for (int i = 0; i < php->size; i++) {printf("%d ", php->arr[i]);}printf("\n");
}

功能：按數組順序打印堆里的元素，方便調試看堆當前存了啥數據。

步驟：

用?for?循環遍歷 ?php->arr??的前 ?php->size??個元素，逐個用 ?printf??輸出，最后換行。

復雜度：

- 時間復雜度：?O(n)??。?n??是堆當前元素個數（?php->size??），循環次數和元素數量成正

比。

- 空間復雜度：?O(1)??。沒額外分配大內存，只是臨時循環變量。

聯系：純調試輔助函數，和堆核心邏輯（增刪調整）沒直接關聯，但調試時，調用

?HPPush?/?HPPop??后，用它打印能直觀看堆數據變化。

4. 交換函數(輔助功能)---Swap函數

void Swap(int* x, int* y) 
{int tmp = *x;*x = *y;*y = tmp;
}

功能：交換兩個?int?變量的值，堆調整（?AdjustUp?/?AdjustDown?）時，父子節點值需要交

換就靠它。

步驟：

用臨時變量 ?tmp??存 ?*x??的值，把 ?*y??賦給 ?*x?，再把 ?tmp?（原來的 ?*x??）賦給 ?*y??。

復雜度：

- 時間復雜度：?O(1)??。固定三步賦值，和變量值無關。

- 空間復雜度：?O(1)??。就一個臨時變量 ?tmp??。

聯系：是 ?AdjustUp??和 ?AdjustDown??的“工具人”，堆調整時發現父子節點值不符合堆序

（大堆/小堆），用它交換值，讓堆序恢復。

5. 堆向上調整函數---AdjustUp函數(核心)

在堆的插入函數和刪除函數(后面會講到)中，我們分別會用到堆向上調整函數和向下調整函數。所

以為了更好的維持代碼的觀賞性以及邏輯合理性。小編專門將堆向上和向下調整的邏輯封裝成函

數。小編會用圖片及文字的形式詳細為大家講解:

在堆的插入函數中:

將新數據插入到數組的尾上，再進行向上調整算法，直到滿足堆。

向上調整算法:

- 先將元素插入到堆的末尾，即最后一個孩子之后

- 插入之后如果堆的性質(滿足大堆或者小堆的順序)遭到破壞，將新插入結點順著其雙親往上調整

到合適位置即可

下面來看一個簡單的例子:

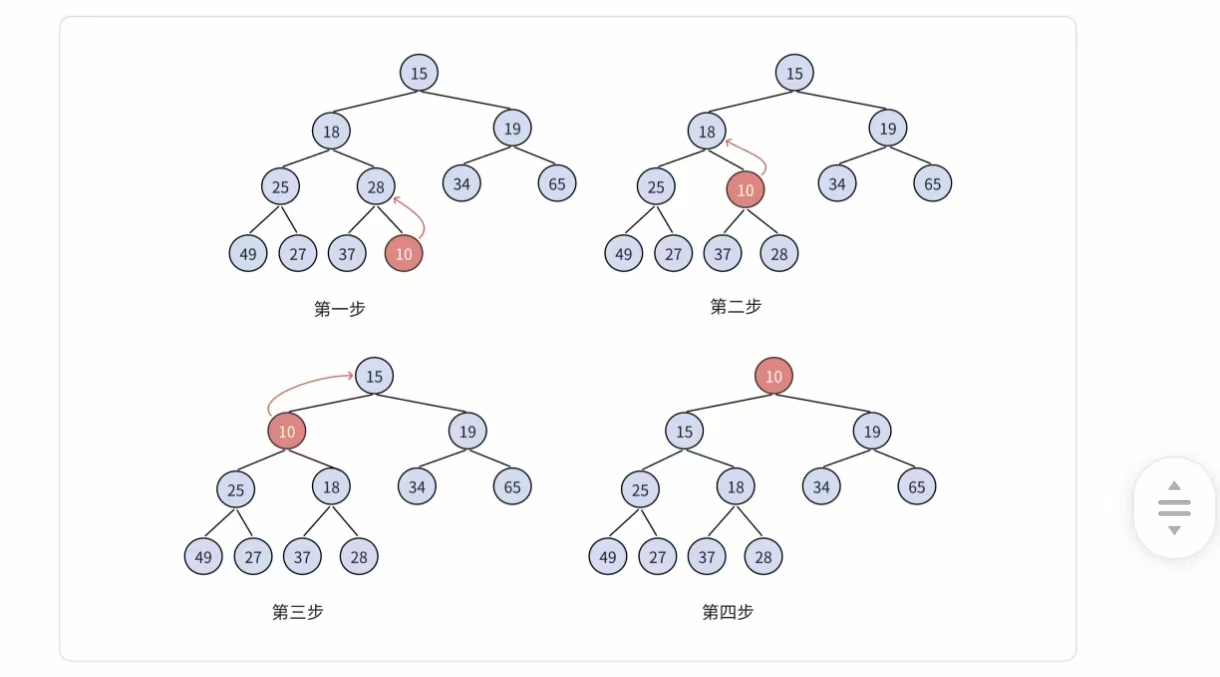
這是堆插入元素時 向上調整（AdjustUp） 的完整過程演示，以“往小堆（父節點值 <?子節

點值）中插入 10?”為例，一步步看新元素如何“上浮歸位”：

初始狀態（插入前）

假設堆原本是一個小堆，結構如下（僅示意關鍵節點）：

- 根是 ?15?，第二層 ?18?、?19?，第三層 ?25?、?28?、?34?、?65??…… 所有父節點值 <?子節點

值，滿足小堆性質(即小堆)。

第一步：插入新元素到末尾

把新數據 ?10??放到堆的數組末尾（對應完全二叉樹的“最后一個葉子節點”位置 ）。此時堆結

構被破壞（?10??比父節點 ?28??小，不滿足大堆“父 <?子” ），需要調整。

第二步：第一次向上調整（和父節點 ?28??比較）

- 新元素 ?10??的下標是 ?child?，計算父節點下標 ?parent = (child-1)/2??→ 找到 ?28?。

- 比較 ?10??和 ?28?：?10 < 28?（小堆要求父 <?子，這里子 <?父，不滿足 ）→ 交換兩者位

置。

- 交換后，?10??跑到 ?28??的位置，?28??下沉到葉子。此時 ?10??的父節點變成 ?18?（繼續檢查

）。

第三步：第二次向上調整（和父節點 ?18??比較）

- 新的 ?child??是 ?18??的下標，重新算 ?parent = (child-1)/2??→ 找到根節點 ?15?？不，這里要

看交換后的層級：

實際步驟是：交換后 ?10??到了原 ?28??的位置，它的新父節點是 ?18?（第二層 ）。

- 比較 ?10??和 ?18?：?10 < 18?（仍不滿足小堆“父 <?子” ）→ 再次交換兩者位置。

- 交換后，?10??跑到 ?18??的位置，?18??下沉到下一層。此時 ?10??的父節點變成 ?15?（根節點

）。

第四步：第三次向上調整（和父節點 ?15??比較）

- 新的 child?是 15?的下標，算 parent = (child-1)/2??→ 父節點不存在（已到根 ）。

- 比較?10??和?15?：?10 < 15?（滿足小堆“父 <?子” ）→ 停止調整。
?
最終，?10??穩定在當前位置，堆重新滿足小堆性質，插入完成。

核心邏輯總結:

向上調整的本質是：新元素從“末尾葉子”開始，不斷和父節點比較，若不滿足堆性質（大堆/

小堆）就交換，直到“父 <?子（小堆）”或“父 >?子（大堆）”，讓新元素“浮”到正確層級。

這一系列交換，保證了插入后堆的結構仍然合法，是堆支持“動態插入”的關鍵！

下面我們來看代碼的實現(先看向上調整函數的實現):

void AdjustUp(HPDataType* arr, int child)
//參數: HPDataType* arr:指向堆數據的數組指針int child  : 插入元素在數組中的下標
{int parent = (child - 1) / 2;while(child > 0){//大堆: >//小堆: <if (arr[child] < arr[parent])   //對應上述例子,若 子<父 ,則二者交換位置{//調整Swap(&arr[child], &arr[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

功能：讓新插入的元素（在?child?位置 ）“往上爬”，直到滿足堆的性質（小堆：子 <?父；

大堆將(子 <?父)改為(子 >?父)即可 ）。

步驟：

1.?計算 ?child??對應的父節點下標 ?parent = (child - 1) / 2??。

2.?循環判斷：只要 ?child > 0?（沒到根節點 ），就比較 ?arr[child]??和 ?arr[parent]??。

- 若子 <?父（小堆情況 ），用 Swap?函數交換兩者值，然后更新 ?child??為 ?parent?，再重新

算新的 ?parent??，繼續往上比較。

- 若子 >?父，說明已滿足堆序， 就break?跳出循環。

復雜度：

- 時間復雜度：?O(log n)??。?n??是堆元素總數，每次調整最多從葉子走到根，路徑長度是堆

的高度。

- 空間復雜度：?O(1)??。就幾個臨時變量（?parent?/?child??），和堆規模無關。

聯系：?HPPush??的核心！?HPPush??把新元素放數組末尾后，調用 ?AdjustUp??讓它“歸

位”，保證插入后堆還是合法的。

需要注意的是上面的這些內容都是使用向上調整函數調整為小堆的邏輯，如果要使用向上調整函數

調整為大堆的呢？要怎樣實現？其實很簡單:? 如果要將堆從小堆改為大堆，核心是修改比較邏輯的

符號，但需要關注兩個關鍵位置：

原小堆的比較條件是? arr[child] <?arr[parent]?（子 <?父 → 交換 ），大堆需要反過來：

void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while(child > 0){// 小堆 → 大堆：把 < 改成 >?if (arr[child] > arr[parent]) ?{Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

修改點：

- 把 ?arr[child] <?arr[parent]??改為 ?arr[child] >?arr[parent]??。

- 含義：當 "子>?父" 時，違反大堆“父 >?子”的規則，需要交換，讓更小的值往上“浮”。

6. 堆插入函數---HPPush函數

void HPPush(HP* php, HPDataType x)
{assert(php);?if (php->size == php->capacity) {?int newCapcity = php->capacity == 0 ? 4 : 2 * php->capacity;?HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapcity * sizeof(HPDataType));?if (tmp == NULL){?perror("realloc fail!");exit(1);?}php->arr = tmp;?php->capacity = newCapcity;?}php->arr[php->size] = x;?AdjustUp(php->arr, php->size);?++php->size;?
}

功能：往堆里加新元素，同時保證堆的結構（大堆/小堆）不變。先處理擴容，再插入、調

整。

步驟：

1.?斷言 ?php??非空（防止傳空指針崩掉 ）。

2.?檢查容量：若 ?size == capacity?，說明數組滿了，需要擴容。

- 擴容策略：原來容量是 0 就開 4 個空間，否則開 ?2 * capacity??個空間。

- 用 ?realloc??重新分配內存，失敗的話打印錯誤并退出。

3.?把新元素 ?x??放到數組末尾（?php->arr[php->size]??位置 ）。

4.?調用 ?AdjustUp?，讓新元素從末尾開始向上調整，恢復堆序。

5.??size++?，更新堆的元素個數。

復雜度：

- 時間復雜度：?O(log n)??。主要耗時在 ?AdjustUp?（?O(log n)??），擴容的 ?realloc??是

?O(n)?（復制原數據 ），但擴容是“均攤”的，整體可視為 ?O(log n)??。

- 空間復雜度：?O(1)?（不考慮擴容的話 ）。但擴容可能新增內存，不過也是為了存數據，通

常分析時，若元素總數是 ?n?，空間復雜度算 ?O(n)?；但函數本身臨時變量是 ?O(1)??。

聯系：是堆“新增元素”的入口，依賴 ?HPInit?（初始化好結構體 ）、?AdjustUp?（調整堆序

），也會觸發 ?HPDestroy??要釋放的動態內存擴容。

7. 判空函數---HPEmpty函數

bool HPEmpty(HP* php) 
{assert(php);return php->size == 0;
}

功能：判斷堆里有沒有元素，返回 ?true?（空）或 ?false?（非空 ）。

步驟：

斷言 ?php??非空，然后返回 ?php->size == 0??的結果。

復雜度：

- 時間復雜度：?O(1)??。直接判斷 ?size??是否為 0 。

- 空間復雜度：?O(1)??。

聯系：在后面介紹的 HPPop?、?HPTop??等函數調用前，常用它判斷堆是否為空，避免操作

空堆出錯。比如HPPop??里 ?assert(!HPEmpty(php))??，依賴它保證合法性。

8. 向下調整函數---AdjustDown函數(核心)

在上面我們詳細介紹了向上調整函數，應用于插入數據函數中，現在我們講解向下調整函數，不同

于之前，這個函數是應用于堆的刪除中的。

在 堆的刪除 函數中:

刪除堆是刪除堆頂的數據，將堆頂的數據跟最后一個數據一換，然后刪除數組最后一個數據，再進

行向下調整算法。

向下調整算法有一個前提：左右子樹必須是一個堆，才能調整。

向下調整算法:

- 將堆頂元素與堆中最后一個元素進行交換

- 刪除堆中最后一個元素

- 將堆頂元素向下調整到滿足堆特性為止

下面我們舉個例子進一步體會刪除數據和向下調整的過程:

?
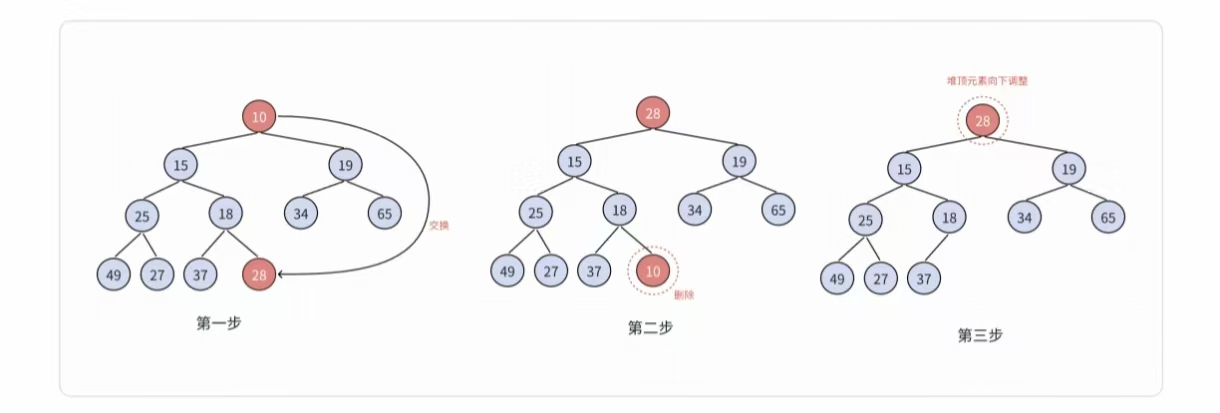
假設堆是 小堆，用數組存儲為：?[10, 15, 19, 25, 18, 34, 65, 49, 27, 28]（對應圖中樹結構，

堆頂是 ?10?，滿足小堆“父 <?子” ）。

堆刪除步驟（小堆版）:? 堆刪除的目標是刪除堆頂元素（?10??），流程分三步：

第一步：交換堆頂和最后一個元素

- 操作：將堆頂（?10?，下標 ?0??）與最后一個元素（?28?，下標 ?9??）交換。

- 結果：

- 數組變為：?[28, 15, 19, 25, 18, 34, 65, 49, 27, 10]?

- 樹結構（對應圖中“第一步”）：堆頂變為 ?28?，原堆頂 ?10??被挪到數組末尾。

第二步：邏輯刪除最后一個元素

- 操作：堆的有效元素個數 ?size??減 1（假設原 ?size=10?，現在 ?size=9??）。

- 結果：

- 數組有效范圍變為前 ?9??個元素：?[28, 15, 19, 25, 18, 34, 65, 49, 27]?

- 原堆頂 ?10??被“邏輯刪除”（后續操作不再訪問 ）。

第三步：判斷當前堆是否滿足小堆結構

交換后，新堆頂（?28??）不滿足小堆“父 <?子”的性質，需要向下調整，讓其“下沉”到正確位

置。交換后，數組有效部分是 ?[28, 15, 19, 25, 18, 34, 65, 49, 27]?（?size=9??），新堆頂是

?28?（下標 ?0??）。

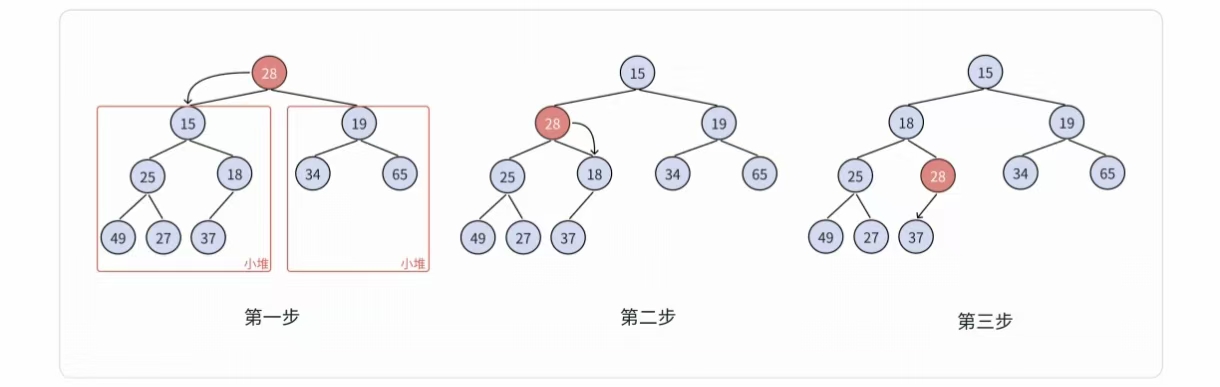
第四步:? 第一次向下調整（對應第二張圖中的第一步）：

- ?parent=0?（值 ?28??），左孩子 ?child=1?（值 ?15??），右孩子 ?child=2?（值 ?19??）。

- 選子節點：小堆選更小的 → ?15 < 19??→ 選左孩子（?child=1??）。

- 父子比較：?28 > 15?（父 > 子，違反小堆“父 <?子” ）→ 交換

- 交換后數組：?[15, 28, 19, 25, 18, 34, 65, 49, 27]?

- 更新 ?parent=1?（原 ?child??位置 ），新 ?child=parent * 2+1=1 * 2+1 = 3?（值 ?25??）。

第五步:? 第二次向下調整（對應第二張圖中的第二步）：

- ?parent=1?（值 ?28??），左孩子 ?child=3?（值 ?25??），右孩子 ?child=4?（值 ?18??）。

- 選子節點：小堆選更小的 → ?18 < 25??→ 選右孩子（?child=4??）。

- 父子比較：?28 > 18?（父 > 子，違反小堆 ）→ 交換

- 交換后數組：?[15, 18, 19, 25, 28, 34, 65, 49, 27]?

- 更新 ?parent=4?（原 child?位置 ）,??新?child=parent * 2+1=4*2+1=9?（超過 ?size=9??，循

環結束 ）。

最終結果（小堆恢復）：

調整后，數組為 ?[15, 18, 19, 25, 28, 34, 65, 49, 27]?，滿足小堆“父節點 ≤ 子節點” 的性質：

- ?15 ≤ 18?、?15 ≤ 19?

- ?18 ≤ 25?、?18 ≤ 28?

- 所有父節點 < 子節點，堆結構恢復。

核心邏輯總結（小堆刪除 + 向下調整）

1.?交換堆頂和末尾：用 ?O(1)??操作避免直接刪堆頂的高成本，把堆頂移到數組末尾。

2.?邏輯刪除末尾：用 ?size--??標記原堆頂為無效，不影響數組結構。

3.?向下調整新堆頂：利用小堆“選更小的子節點、父大則交換”的邏輯，讓新堆頂（原末尾元

素 ）下沉到正確位置，恢復“父 ≤ 子”的小堆性質。

講完了上面的例子，下面我們來看向下調整函數代碼的實現

void AdjustDown(HPDataType* arr, int parent, int n) 
//參數: HPDataType* arr: 指向存儲堆數據數組的指針
//      int parent : 起始父節點在數組中的下標     
//      int n : 堆中有效數據元素的個數 
{int child = parent * 2 + 1;   //左孩子while (child < n) { //小堆: >//大堆: <if (child + 1 < n && arr[child] > arr[child + 1]) { child++; }//小堆: <//大堆: >if (arr[child] < arr[parent]) { Swap(&arr[child], &arr[parent]); parent = child;             child = parent * 2 + 1;     } else {break; }}
}

功能：讓 ?parent??位置的元素“往下沉”，直到滿足堆序（對應上述圖片例子中的小堆為例

）。常用于刪除堆頂、構建堆場景。

步驟：

1.?先選左孩子 ?child = parent * 2 + 1??。

2.?循環判斷 ?child < n?（在有效范圍 ）：

- 若右孩子存在（?child + 1 < n??）且右孩子值更小，選右孩子（?child++??）。

- 比較 ?child??和 ?parent??的值：若子 <?父，交換兩者，更新 ?parent??為 ?child?，重新算新

的 ?child??，繼續往下調整。

- 若子 < 父，滿足堆序， 就會 break跳出? 。

復雜度：

- 時間復雜度：?O(log n)??。從父節點往下調整，最多走到葉子，路徑長度是堆高度

（?~log?n??）。

- 空間復雜度：?O(1)??。就幾個臨時變量（?child?/?parent??）。

聯系：?HPPop??的核心！刪除堆頂時，把最后一個元素放堆頂，然后調用 ?AdjustDown??讓

它“下沉”，恢復堆結構。

上述代碼是關于向下調整小堆的過程，那么要是向下調整大堆呢？

要把適配小堆的向下調整函數改為適配大堆，核心是調整選子節點的邏輯和父子交換的條

件，以下是具體步驟和對比：

小堆 → 大堆：核心邏輯差異:

堆類型 選子節點目標 選子節點條件（對比左右子節點） 父子交換條件（觸發調整）?

小堆: 父節點盡可能小 選更小的子節點（?左 > 右 → 選右?） 子節點 < 父節點時交換?

大堆: 父節點盡可能大 選更大的子節點（?左 < 右 → 選右?） 子節點 > 父節點時交換?

改為大堆，需要修改兩處核心邏輯：

1. 選子節點：找“更大的子節點”

把小堆的“選更小的子節點”條件，改為“選更大的子節點”：

// 大堆：選更大的子節點 → 條件改為 arr[child] < arr[child + 1]
if (child + 1 < n && arr[child] < arr[child + 1]) { ?child++; ?
}

- 邏輯：如果右子節點比左子節點大（?arr[child] < arr[child + 1]??），就選右子節點（讓父

節點和更大的子節點比較，保證父節點盡可能大 ）。

2. 父子交換條件：子節點 > 父節點時交換

把小堆的“子節點 < 父節點時交換”，改為“子節點 > 父節點時交換”：?

// 大堆：子節點 > 父節點時交換 → 條件改為 arr[child] > arr[parent]
if (arr[child] > arr[parent]) { ?Swap(&arr[child], &arr[parent]); ?parent = child; ?child = parent * 2 + 1; ?
} else {break; ?
}

- 邏輯：當子節點值大于父節點值時，違反大堆“父節點 >??子節點”的規則，需要交換，讓父節

點變大。

修改后，適配大堆的向下調整函數：

void AdjustDown(HPDataType* arr, int parent, int n) 
//參數: HPDataType* arr: 指向存儲堆數據數組的指針
//      int parent : 起始父節點在數組中的下標     
//      int n : 堆中有效數據元素的個數   
{    int child = parent * 2 + 1; ?// 左孩子下標while (child < n) { ?// 1. 大堆：選更大的子節點if (child + 1 < n && arr[child] < arr[child + 1]) { ?child++; ?// 右孩子更大，選右孩子}// 2. 大堆：子節點 > 父節點時交換（保證父 ≥ 子）if (arr[child] > arr[parent]) { ?Swap(&arr[child], &arr[parent]); ?parent = child; ?// 繼續向下調整child = parent * 2 + 1; ?} else {break; ?// 父 ≥ 子，滿足大堆性質，退出}}
}

9. 堆刪除函數(刪除堆頂)---HPPop函數

void HPPop(HP* php) 
//參數: 指向堆刪除結構HP的指針
{assert(!HPEmpty(php));?Swap(&php->arr[0], &php->arr[php->size - 1]);?--php->size;?AdjustDown(php->arr, 0, php->size);?
}

功能：刪除堆頂元素（大堆里的最大值/ 小堆里的最小值），并調整堆結構，保證刪除后還是

合法堆。

步驟：

1.?斷言堆非空（?!HPEmpty(php)??），空堆刪元素會出錯。

2.?交換堆頂（?arr[0]??）和最后一個元素（?arr[size - 1]??）。

3.??size--?，把原來的堆頂元素“移出”有效范圍。物理上沒刪, 只是在邏輯上不屬于堆結構了。

4.?調用 ?AdjustDown?，從新的堆頂（?arr[0]??）開始向下調整，恢復堆序。

復雜度：

- 時間復雜度：?O(log n)??。主要耗時在 ?AdjustDown?（?O(log n)??）。

- 空間復雜度：?O(1)??。

聯系：依賴 ?HPEmpty?（判空 ）、?Swap?（交換 ）、?AdjustDown?（調整 ），是堆“刪除

最優先元素（堆頂）”的關鍵操作。?

10. 取堆頂函數---HPTop函數

HPDataType HPTop(HP* php) 
{assert(!HPEmpty(php));?return php->arr[0];?
}

功能：獲取堆頂元素（大堆里的最大值/小堆里的最小值?），方便用戶查看堆的“最優先數

據”。

步驟：

斷言堆非空，然后返回 ?arr[0]??的值（堆頂元素 ）。

復雜度：

- 時間復雜度：?O(1)??。直接訪問數組第一個元素。

- 空間復雜度：?O(1)??。

聯系：是堆“查最優先元素”的接口，常和 ?HPPop??配合，比如取堆頂后刪除，實現“獲取并

刪除”邏輯。

函數間整體聯系:

1.?初始化與銷毀：?HPInit??初始化堆，?HPDestroy??銷毀堆，是堆生命周期的“開始”和“結束”。

2.?增刪操作：

- ?HPPush??依賴 ?AdjustUp??完成插入后調整；

- ?HPPop??依賴 ?Swap??交換堆頂和末尾、?AdjustDown??完成刪除后調整。

3.?輔助與工具：

- ?Swap??給 ?AdjustUp?/?AdjustDown??提供交換能力；

- ?HPEmpty??給 ?HPPop?/?HPTop??提供判空保護；

- ?HPPrint??用于調試，查看堆數據。

這些函數相互配合，實現了 堆的完整功能：初始化 → 插入 → 調整 → 刪除 → 銷毀，覆蓋了堆作

為“優先隊列”的核心操作（快速存取最優先元素 ）。

簡單說，它們圍繞“動態數組模擬堆結構，靠調整函數（?AdjustUp?/?AdjustDown??）維持堆序”這個

核心，分工完成初始化、增、刪、查、銷毀等任務，讓堆能作為獨立數據結構被使用 。

1.3 測試文件(test.c)

#include"Heap.h"
void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);//HPPush(&hp, 70);//HPPush(&hp, 25);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPDestroy(&hp);
}void test02()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDestroy(&hp);
}int main()
{test01();test02();return 0;
}

這份測試代碼主要是驗證堆的基本操作是否正確，核心流程可以簡單總結為：

1. 測試內容

通過兩個函數（?test01??和 ?test02?）測試堆的 初始化、插入、刪除堆頂、取堆頂、判空、銷毀 等

功能。

2. 關鍵操作解析

- ?test01?：

- 先初始化堆，插入 ?56、10、15、30??四個數據（插入時會自動調整為大堆/小堆結構）。

- 每次調用 ?HPPop??刪除堆頂元素后，用 ?HPPrint??打印堆的當前狀態，直觀查看刪除后堆的變

化。

- 最后銷毀堆釋放資源。

- ?test02?：

- 同樣插入四個數據，然后用循環（?while (!HPEmpty)?）持續取堆頂元素（?HPTop?）并打印，同

時刪除堆頂（?HPPop?），直到堆空。

- 目的是驗證“取頂+刪除”的循環操作是否符合堆的特性（比如大堆會依次輸出最大值，小堆依次輸

出最小值）。

3. 核心邏輯

- 堆的插入（?HPPush?）會通過“向上調整”維持堆結構（大堆/小堆）。

- 堆的刪除（?HPPop?）會通過“交換堆頂和末尾元素→刪除末尾→向下調整”恢復堆結構。

- 測試代碼通過打印和輸出，驗證這些操作是否正確執行。

簡單說：這段代碼就是用實際數據“跑一遍”堆的增刪查流程，看結果是否符合預期（比如大堆每次

刪最大，小堆每次刪最小）。

下面小編版完整版的代碼留給大家:

1.4 完整代碼

1. 頭文件---Heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//堆的結構
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;     //有效數據個數int capacity; //空間大小
}HP;//交換函數
void Swap(int* x, int* y);
//向上調整函數
void AdjustUp(HPDataType* arr, int child);
//向下調整函數
void AdjustDown(HPDataType* arr, int parent, int n);//初始化函數
void HPInit(HP* php);
//銷毀函數
void HPDestroy(HP* php);
//打印函數
void HPPrint(HP* php);//插入函數
void HPPush(HP* php, HPDataType x);
//刪除函數
void HPPop(HP* php);
//取堆頂數據
HPDataType HPTop(HP* php);// 判空函數
bool HPEmpty(HP* php);

2. 實現文件---Heap.c

#include"Heap.h"void HPInit(HP* php)
{php->arr = NULL;php->size = php->capacity = 0;
}
void HPDestroy(HP* php)
{if (php->arr)free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆：>//小堆：<if (arr[child] < arr[parent]){//調整Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}
void HPPush(HP* php, HPDataType x)
{assert(php);//判斷空間是否足夠if (php->size == php->capacity){int newCapcity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapcity*sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newCapcity;}php->arr[php->size] = x;//向上調整AdjustUp(php->arr, php->size);++php->size;
}
// 判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}
//向下調整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){//小堆：>//大堆：<if (child + 1 < n && arr[child] > arr[child + 1]){child++;}//小堆: <//大堆：>if (arr[child] < arr[parent]){//調整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
void HPPop(HP* php)
{assert(!HPEmpty(php));// 0 php->size-1Swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下調整AdjustDown(php->arr, 0, php->size);
}//取堆頂數據
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}

3. 測試文件---test.c

#include"Heap.h"
void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);//HPPush(&hp, 70);//HPPush(&hp, 25);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPDestroy(&hp);
}void test02()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDestroy(&hp);
}int main()
{test01();test02();return 0;
}

以上便是關于整個堆的實現內容，總體來說還是挺有難度的。特別是向上調整函數和向下調整函數

在堆插入函數和堆刪除函數中的作用，值得大家反復理解和思考。后面還有關于堆的一個重要板塊

——堆排序，即利用數據結構堆的思想來進行數據排序。小編會在下一篇文章中為大家進行講解。

好了，最后感謝大家的觀看！如果在寫的過程中發現小朋友問題，也歡迎在評論區中指出！感謝大

家的觀看！