粒子群算法（PSO算法）

粒子群算法概述

1.粒子群優化算法（Particle Swarm Optimization，簡稱PSO）。粒子群優化算法是在1995年由Kennedy博士和Eberhart博士一起提出的，它源于對鳥群捕食行為的研究。

2.基本核心是利用群體中的個體對信息的共享從而使得整個群體的運動在問題求解空間中產生從無序倒有序的演化過程，從而獲得問題的最優解。

3.粒子群算法模擬鳥群的捕食過程，將待優化的問題看做是捕食的鳥群，解空間看做是鳥群的飛行空間，空間的每只鳥的位置即是粒子群算法在解空間的一個粒子，也就是待優化問題的一個解。

粒子群算法滿足以下假設：

1.粒子被假定沒有體積沒有質量，本身的屬性只有速度和位置。

2.每個粒子在解空間中運動，它通過速度改變其方向和位置。

3.通常粒子將追蹤當前的最優粒子以經過最少代數的搜索達到最優。

PSO算法模型

1.PSO算法首先在可行解空間中初始化一群粒子，每個粒子都代表極值最優化問題的一個潛在最優解，用位置、速度和適應度值三項指標表示該粒子的特征。

2.粒子在解空間中運動，通過跟蹤個體極值Pbest和群體極值Gbest來更新個體位置。

3.粒子每更新一次位置和速度，就計算一次適應度值，并且通過比較新粒子的適應度值和個體極值、群體極值的適應度更新個體極值Pbest和群體極值Gbest的位置。

假設在一個n維的搜索空間，有m個粒子組成一個粒子群 ${X}=\left ( X{_{1}},X_{2},...,X_{m} \right )$ ，其中：

注：

掌握PSO算法需要從以下兩個角度進行理解：

1.粒子在一定程度上離開原先的搜索軌跡，向新的方向進行搜索，體現了一種向未知區域開拓的能力，類似于全局搜索。

2.粒子在一定程度上繼續在原先的搜索軌跡上更細一步的搜索，主要針對搜索過程中所搜索到的區域進行更進一步的搜索，類似于局部搜索。

基本粒子群算法

在找到這兩個最優解時，粒子根據下面的式子來更新自己的速度和位置：

?注：

Vij 指第i個粒子在第j個分量的速度，k代表第k次循環。r1和r2是介于（0,1）的隨機數。c1和c2是學習因子。

關于學習因子c1和c2：

1.如果c1=c2=0，則說明粒子將以當前的飛行速度飛到邊界。此時，粒子僅能搜索有限的區域，所以很難找到最優解。

2.如果c1=0，則為“社會”模型，粒子只有群體經驗而缺乏認知能力。此時，算法收斂速度快，但容易陷入局部最優。

3.如果c2=0，則為“認知”模型，粒子沒有社會共享信息，粒子之間沒有信息的交互。此時，算法找到最優解的概率很小。

易知該公式由三部分組成：

1.第一部分為“慣性(inertia)”或“動量(momentum)”部分，反映了粒子的運動“習慣(habit)”，代表粒子有維持自己先前速度的趨勢。

2.第二部分為“認知(cognition)”，反映了粒子對自身歷史經驗的記憶(memory)或回憶(remembrance)，代表粒子有向自身歷史最佳位置逼近的趨勢。

3.第三部分為“社會(social)”部分，反映了粒子間協同合作與知識共享的群體歷史經驗，代表粒子有向群體或者鄰域歷史最佳位置逼近的趨勢。

標準粒子群算法

Shi和Eberhart于1998年在IEEE國際計算學術會議上發表了題為“A Modified Particle Swarm Optimizer”的論文，首次在速度更新公式中加入了慣性權重，如下式所示：

?其中w>0叫做慣性因子。w越大，全局尋優能力越強，局部尋優能力越弱；w越小，全局尋優能力越弱，局部尋優能力越強。此時的粒子群算法被稱作是標準粒子群算法。

經驗：

實驗表明，動態的w能獲得更好的尋優結果。在搜索過程中可以對w進行動態調整：可以初始給w賦子較大正值，隨著搜索的進行，可以線性地使逐漸減小，這樣可以保證在算法開始時，各粒子能夠以較大的速度步長在全局范圍內探測到較好的區域：而在搜索后期，較小的值則保證粒子能夠在極值點周圍做精細的搜索，從而使算法有較大的概率向全局最優解位置收斂。對W進行調整，可以權衡全局搜索和局部搜索能力。

目前，采用較多的動態慣性權重值是線性遞減權值策略，其表達式如下：

?其中， $T_{max}$ 表示最大迭代次數； $w_{max}$ 和 $w_{min}$ 分別表示最大和最小慣性權重。在大多數應用中，通常有 $w_{max}=0.9$ ?,? $w_{min}=0.4$ ?。

當然，除了線性遞減權值策略，還有線性微分遞減策略：

?壓縮粒子群算法

當? $w=\lambda$ ?時，標準粒子算法就會退化為壓縮粒子群算法：

此時的粒子群算法被稱作是壓縮粒子群算法。其中? $\lambda$ ?為壓縮因子：

?離散粒子群算法

基本粒子群算法是在連續域中搜索函數極值的有利工具。為了處理離散空間的問題，Kennedy和Eberhart又提出了一種離散二進制版的粒子群算法。在此算法中，將離散空間問題映射到連續粒子空間，并適當修改粒子群算法來求解。在計算上仍保留經典粒子群算法中的速度和位置更新規則。

在離散粒子群算法中，將離散問題空間映射到連續粒子運動空間，并做適當的修改。仍然保留經典粒子群算法中的速度和位置更新規則。粒子在狀態空間的取值只限于0，1兩個值，而速度的每一個位代表的是粒子位置所對應的位取值為0/1的可能性。因此在離散粒子群算法中，粒子速度的更新公式依然保持不變，但是個體最優位置和全局最優位置每一位的取值只能為0/1。

更新方式：

?，

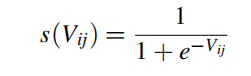其中，r ~ U(0 , 1) ,?? $V_{ij}$ ?表示位置 $X_{ij}$ 取值為1的可能性，其更新公式與基本粒子群算法一致。

粒子群算法流程

Step 1.種群初始化：群體規模 $N$ ，每個粒子的位置 $X$ 和速度 $V_{i}$ 。

Step 2.計算每個粒子的適應值 $fit_{i}$ ;。?

Step 3.對每個粒子，用它的適應度值 $fit_{i}$ 和個體極值 $Pbest_{i}$ 比較。如果 $fit_{i}<Pbest_{i}$ ，則用 $fit_{i}$ 替換 $Pbest_{i}$ 。

Step 4.對每個粒子，用它的適應度值 $fit_{i}$ 和全局極值 $Gbest_{i}$ 比較。如果 $fit_{i}<Gbest_{i}$ ，則用 $fit_{i}$ 替換 $Gbest_{i}$ 。

Step 5.迭代更新粒子的速度 $V_{i}$ 和位置 $X$ 。

Step6.進行邊界條件處理。

Step 7.判斷算法終止的條件是否滿足。若滿足，則結束算法并輸出優化結果；否則，返回Step2。

?算法的參數說明

?注：

邊界條件處理：

當某一維或若干維的位置或速度超過設定值時，采用邊界條件處理策略可將粒子的位置限制在可行搜索空間內，這樣能避免種群的膨脹與發散，也能避免粒子大范圍地盲目搜索，從而提高了搜素效率。具體的方法有很多種，比如通過設置最大位置限制 $x_{max}$ 和最大速度限制 $v_{max}$ ，當超過最大位置或最大速度時，在范圍內隨機產生一個數值代替，或者將其設置為最大值，即邊界吸收。

例題

適應度函數fit.m

function y = fit(x)
% 函數用于計算粒子的適應度
% x:輸入粒子
% y:粒子適應度值
y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

主腳本main.m

%% I. 清空環境
clc
clear
close all%% II. 繪制目標函數曲線
figure
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
mesh(x,y,z)
hold on%% III. 參數初始化
c1 = 1.49445;
c2 = 1.49445;kmax = 100;   % 進化次數  
popsize = 100; %種群規模% 控制粒子速度
Vmax = 1;
Vmin = -1;
% 個體位置變化的最大范圍
popmax = 5;
popmin = -5;%% IV. 產生初始粒子和速度
for i = 1:popsize% 隨機產生一個種群pop(i,:) = 5*rands(1,2);     %初始各個粒子位置V(i,:) = rands(1,2);         %初始化各個粒子速度% 計算適應度fitness(i) = fit(pop(i,:));   %各個粒子的適應度值
end%% V. 個體極值和群體極值
[best_fitness best_index] = max(fitness);
Gbest = pop(best_index,:);     %粒子群體最優位置
Pbest = pop;                   %粒子個體最優位置
fitnessPbest = fitness;        %粒子個體最優適應度值
fitnessGbest = best_fitness;   %粒子群體最優適應度值%% VI. 迭代尋優
for i = 1:kmaxfor j = 1:popsize% 速度更新V(j,:) = V(j,:) + c1*rand*(Pbest(j,:) - pop(j,:)) + c2*rand*(Gbest - pop(j,:));% 進行速度約束(邊界約束)V(j,find(V(j,:)>Vmax)) = Vmax;V(j,find(V(j,:)<Vmin)) = Vmin;% 位置更新pop(j,:) = pop(j,:) + V(j,:);% 進行位置約束(邊界約束)pop(j,find(pop(j,:)>popmax)) = popmax;pop(j,find(pop(j,:)<popmin)) = popmin;% 適應度值更新fitness(j) = fit(pop(j,:)); endfor j = 1:popsize  % 個體最優更新if fitness(j) > fitnessPbest(j)Pbest(j,:) = pop(j,:);fitnessPbest(j) = fitness(j);end% 群體最優更新if fitness(j) > fitnessGbestGbest = pop(j,:);fitnessGbest = fitness(j);endend Best(i) = fitnessGbest;%用于存儲每次迭代產生的最優的適應度值        
end
%% VII.輸出結果
[fitnessGbest, Gbest]
plot3(Gbest(1), Gbest(2), fitnessGbest,'bo','linewidth',1.5)figure
plot(Best)
title('最優個體適應度','fontsize',12);
xlabel('進化代數','fontsize',12);ylabel('適應度','fontsize',12);

運行結果：

ans =80.7065   -4.5223    4.5231

?適應度函數fun.m

function y = fun(x)
%函數用于計算粒子適應度值
%x：輸入粒子 
%y：粒子適應度值 
y = 0.5 + (sin(sqrt(x(1)^2+x(2)^2))^2 - 0.5) / (1 + 0.001*(x(1)^2+x(2)^2))^2;
% y = 3*cos(x(1)*x(2)) + x(1) + x(2)^2;

主腳本main.m

%% I. 清空環境
% clc
% clear%% II. 繪制目標函數曲線
figure
[x,y] = meshgrid(-10:0.1:10,-10:0.1:10);
z = 0.5 + (sin(sqrt(x.^2+y.^2)).^2 - 0.5)./ (1 + 0.001*(x.^2+y.^2)).^2;
mesh(x,y,z)
hold on
%% III. 參數初始化
c1 = 1.49445;
c2 = 1.49445;kmax = 100;   % 進化次數
popsize = 100; %種群規模% 控制粒子速度
Vmax = 1;
Vmin = -1;
% 個體位置變化的最大范圍
popmax = 10;
popmin = -10;%慣性權重最大值和最小值
Wmax = 0.9;
Wmin = 0.4;% %壓縮因子
% phi = c1+c2;
% lamda = 2 / abs(2 - phi - sqrt(phi^2 - 4*phi));   % 壓縮因子
%% IV. 產生初始粒子和速度
for i = 1:popsize% 隨機產生一個種群pop(i,:) = 10*rands(1,2);     %初始各個粒子位置V(i,:) = rands(1,2);         %初始化各個粒子速度% 計算適應度fitness(i) = fun(pop(i,:));   %各個粒子的適應度值
end%% V. 個體極值和群體極值
[best_fitness best_index] = min(fitness);
Gbest = pop(best_index,:);     %粒子群體最優位置
Pbest = pop;                   %粒子個體最優位置
fitnessPbest = fitness;        %粒子個體最優適應度值
fitnessGbest = best_fitness;   %粒子群體最優適應度值%% VI. 迭代尋優
for i = 1:kmax%計算動態慣性權重w = Wmax - (Wmax - Wmin)*i / kmax;for j = 1:popsize% 速度更新V(j,:) = w*V(j,:) + c1*rand*(Pbest(j,:) - pop(j,:)) + c2*rand*(Gbest - pop(j,:));%標準粒子群算法%         V(j,:) = lamda*V(j,:) + c1*rand*(Pbest(j,:) - pop(j,:)) + c2*rand*(Gbest - pop(j,:));%壓縮粒子群算法%         V(j,:) = V(j,:) + c1*rand*(Pbest(j,:) - pop(j,:)) + c2*rand*(Gbest - pop(j,:));%普通粒子群算法% 進行速度約束(邊界約束)V(j,find(V(j,:)>Vmax)) = Vmax;V(j,find(V(j,:)<Vmin)) = Vmin;% 位置更新pop(j,:) = pop(j,:) + V(j,:);% 進行位置約束(邊界約束)pop(j,find(pop(j,:)>popmax)) = popmax;pop(j,find(pop(j,:)<popmin)) = popmin;% 適應度值更新fitness(j) = fun(pop(j,:));endfor j = 1:popsize% 個體最優更新if fitness(j) < fitnessPbest(j)Pbest(j,:) = pop(j,:);fitnessPbest(j) = fitness(j);end% 群體最優更新if fitness(j) < fitnessGbestGbest = pop(j,:);fitnessGbest = fitness(j);endendBest(i) = fitnessGbest;%用于存儲每次迭代產生的最優的適應度值
end
%% VII.輸出結果
disp(['當x=',num2str(Gbest(1)),'和','y=',num2str(Gbest(2)),'時','所求函數的最小值是',num2str(fitnessGbest)])plot3(Gbest(1), Gbest(2), fitnessGbest,'bo','linewidth',15)figure
plot(Best)
title('最優個體適應度','fontsize',12);
xlabel('進化代數','fontsize',12);ylabel('適應度','fontsize',12);

運行結果：

>> main
當x=7.2595e-06和y=-1.7485e-05時所求函數的最小值是3.5877e-10