寫在前面：進入新一輪學習階段，從閱讀開始。
本文分享的是WWW2025收錄的與作者研究相近的graph-based xx相關paper的閱讀筆記，含個人理解，僅供參考😄

0x01 HEI：利用不變性原理實現異配圖結構分布偏移學習

Jinluan Yang, et al. Leveraging Invariant Principle for Heterophilic Graph Structure.（浙大）

1.1 摘要

異配圖神經網絡（Heterophilic graph neural networks, HGNNs）在圖的半監督學習任務中表現出了良好的效果。值得注意的是，大多數現實世界中的異配圖是由不同鄰接模式的節點混合而成的，呈現出局部節點級別的同配（Homophilic）和異配結構。

然而，現有的研究僅致力于設計更好的統一的HGNN架構，以同時用于異配和同配圖上的節點分類任務，弄且它們對HGNN性能關于節點的分析僅基于已確定的數據分布，而沒有探索由于訓練節點和測試節點的結構模式差異所導致的影響。如何在異配圖上學習不變的節點表示以處理這種結構差異活分布變化仍未得到探索。

在本文中，我們首先從數據增強的角度討論了以往基于圖的不變學習方法在解決異配圖結構分布偏移的局限性。
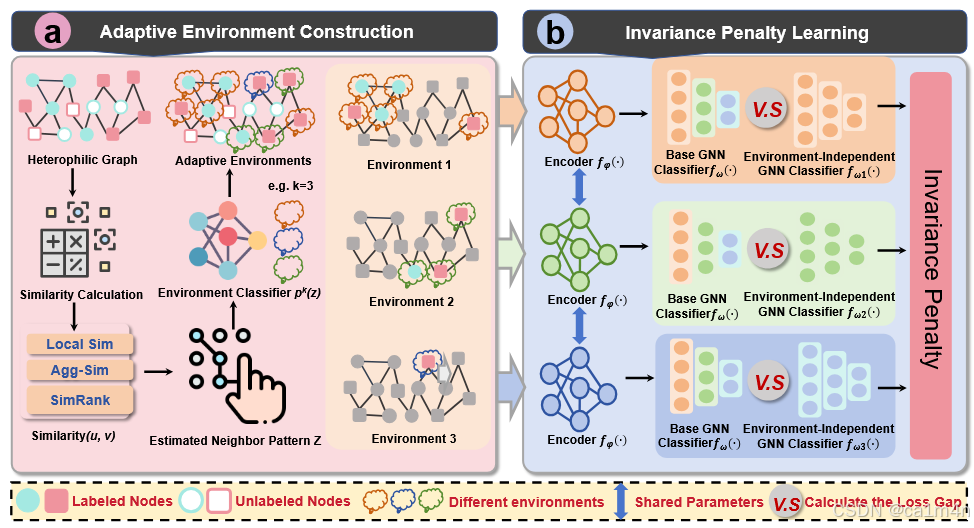
然后，我們提出了HEI這一框架，它能夠通過整合異配信息（即節點的估計鄰接模式）來生成不變的節點表示，從而在無需擴充數據的情況下推斷出潛在環境，并用于不變性預測。
我們提供了詳細的理論保證以闡明HEI的合理性。在各種基準測試和骨干網絡上的大量實驗也表明，與現有的SOTA基線相比，我們的方法具有有效性和魯棒性。

開源代碼：HEI

1.2 背景與動機

異配圖結構分布偏移（Heterophilic Graph Structure distribution Shift, HGSS）：一種全新的數據分布偏移視角，用于重新審視現有的HGNNs工作。

盡管前景可觀，但大多數先前的HGNNs假設節點共享已確定的數據分布，我們認為不同鄰接模式的節點之間存在數據分布差異。如圖1（a1）所示，異配圖由具有局部同配性和異配性結構的節點混合組成，即節點具有不同的鄰接模式。節點的鄰接模式可以通過節點同配性來衡量，通過比較節點與其鄰接節點的標簽來表示同配水平。在此，我們將訓練節點和測試節點之間不同的鄰接模式識別為異配圖結構分布偏移（圖1（a2））。這種偏移在先前的工作中被忽視，但實際上影響了GNN的性能。如圖1（a3）所示，我們在Squirrel數據集上可視化了訓練節點和測試節點之間的HGSS。與測試節點相比，訓練節點更傾向于高同配性，這可能導致測試性能下降。
值得注意的是，盡管一些近期的研究也探討了同配和異配結構模式，但到目前為止，它們尚未為這一問題提供明確的技術解決方案。與專注于backbone設計的傳統HGNN研究相比，從數據分布的角度尋求解決方案以解決HGSS問題顯得尤為迫切。

現有基于圖的不變性學習（Invariant learning）方法由于采用了基于擴充的環境構建策略，在處理HGSS問題時表現不佳。
在一般分布變化的背景下，不變性學習技術因其在減輕這方面的有效性越來越受到認可。其基本方法是學習節點表示，以促進在各種構建環境中進行不變性預測器的學習（圖1（b1）），遵循風險外推（Risk Extrapolation, REx）原則。不幸的是，之前的基于圖的不變學習方法可能無法有效地解決HGSS問題，主要是因為明確的環境可能對不變性學習無效。如（圖1（c1））所示，在HGSS設置中，改變原始結構并不總是能影響節點的鄰接模式。實際上，獲得與鄰域模式相關的最優且多樣的環境是具有挑戰性的。我們的觀察（圖1（c2））表明，EERM，一種利用環境擴充來解決節點級任務中的圖分布變化的開創性不變性學習方法，在HGSS設置下表現不佳。有時，其改進效果還不如直接采用原始的V-Rex方法，后者是通過將訓練節點隨機分布在不同的環境組中實現的。我們將這種現象歸因于不合理的環境構建。根據我們的分析，EERM實質上是V-Rex的節點環境增強版，即它們之間的性能差異僅僅被不同的環境構建策略影響。
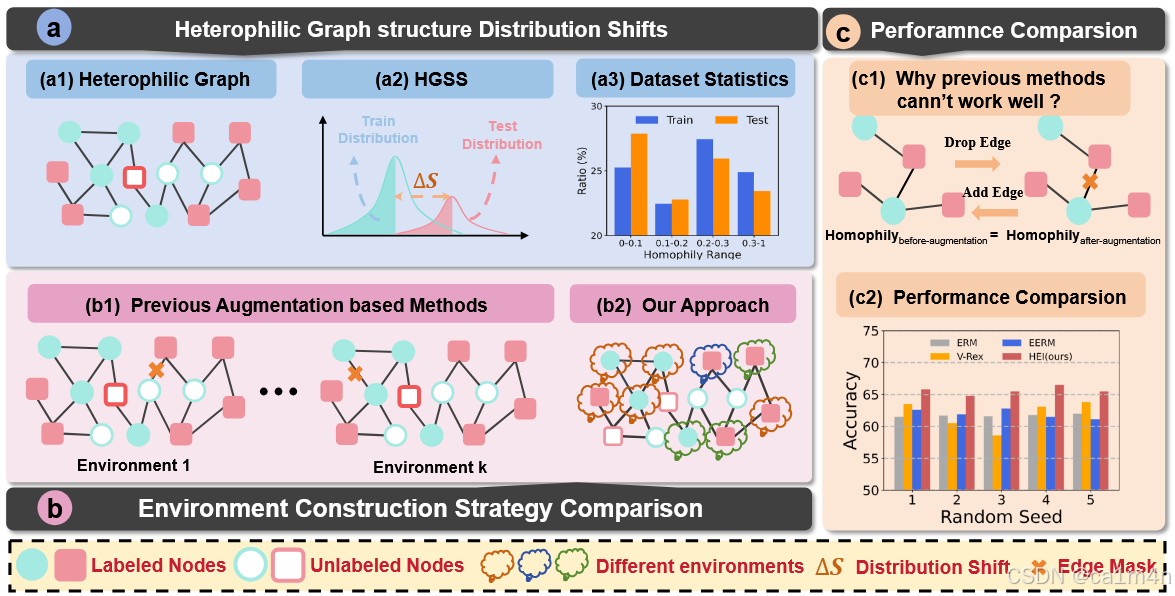圖1：（a）展示了異配圖結構分布偏移，其中圖表和直方圖顯示了HGSS以及鄰接模式在Squirrel數據集上的訓練節點與測試節點之間的差異；（b）展示了先前不變學習工作與我們方法在數據增強方面不同環境構建策略的比較；（c）表明先前方法的環境構建可能無法有效解決HGSS，因為鄰接模式未發生變化。傳統方法與基于圖的不變學習方法之間的實驗結果可支持我們的分析并驗證我們提出的HEI的優越性。

在訓練階段，我們如何確定一個合適的指標來估計節點的鄰域模式，并利用它來推斷潛在環境以解決HGSS問題。

1.3 Contributions

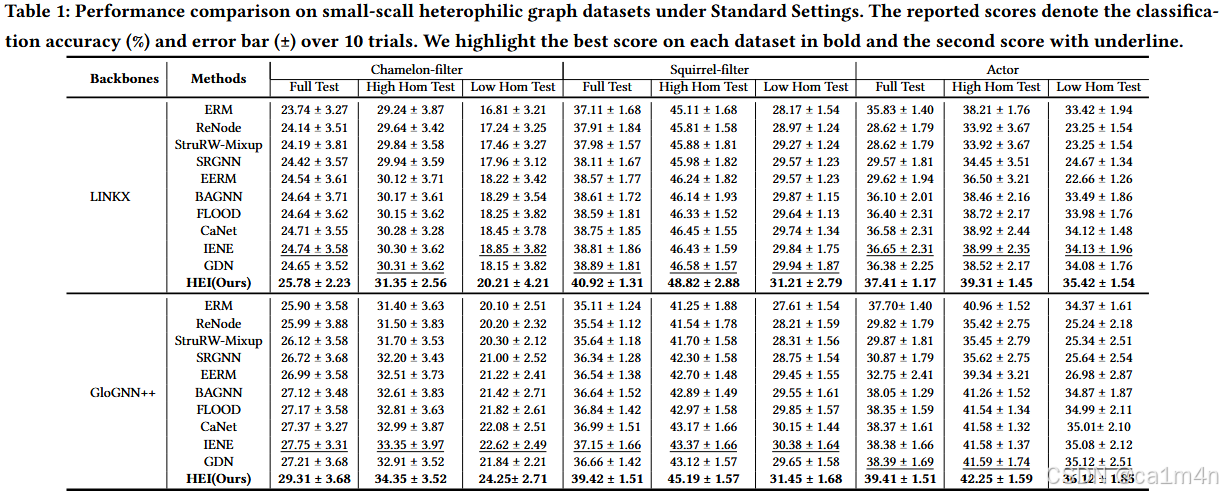
1. New Issue. 強調了一個重要但常被忽視的異配圖結構分布偏移（HGSS），這與大多數專注于backbone設計的異配圖神經網絡的研究不同；
2. New Framework. 提出了HEI，一種新穎的基于圖的不變學習框架，用于解決HGSS問題。與以往不同的是，我們的方法強調利用節點固有的異配信息來推斷潛在環境，無需進行增強操作，從而顯著提高了HGNN的泛化能力和性能；
3. Exp. 在多個基準和骨干結構上展示了HEI的有效性。

即，異配圖上的OOD泛化，構建環境時利用同配性（結構級別）指標進行構建，先前工作基本是節點級別。

0x02 SmoothGNN：一種用于無監督節點異常檢測的平滑感知GNN

Xianyu Dong, et al. SmoothGNN: Smoothing-aware GNN for Unsupervised Node Anomaly Detection. （港中文）

2.1 摘要

在圖學習中出現的平滑問題會導致節點表示無法區分，這給與圖相關任務帶來了巨大挑戰。
然而，我們的實驗表明，這個問題能夠揭示節點異常檢測（Node Anomaly Detection, NAD） 中先前研究所忽略的潛在特性。我們引入了個體平滑模式（Individual Smoothing Patterns, ISP）和鄰域平滑模式（Neighborhood Smoothing Patterns, NSP），這表明異常節點的表示比正常節點的表示更難進行平滑處理。此外，我們探討了這些模式的理論意義，展示了ISP和NSP對NAD任務的潛在益處。

受這些發現的啟發，我們提出了SmoothGNN，這是一種新穎的無監督節點異常檢測框架。
首先，我們設計了一個學習組件來明確捕捉ISP以檢測節點異常。
其次，我們設計了一個譜神經網絡來隱式學習ISP以增強檢測能力。
最后，我們根據我們的發現設計了一個有效的系數，使得NSP可以作為節點表示的系數，有助于識別異常節點。
此外，我們設計了一種新穎的異常度量方法，用于計算節點的損失函數和異常得分，該方法利用ISP和NSP來反映NAD的特性。
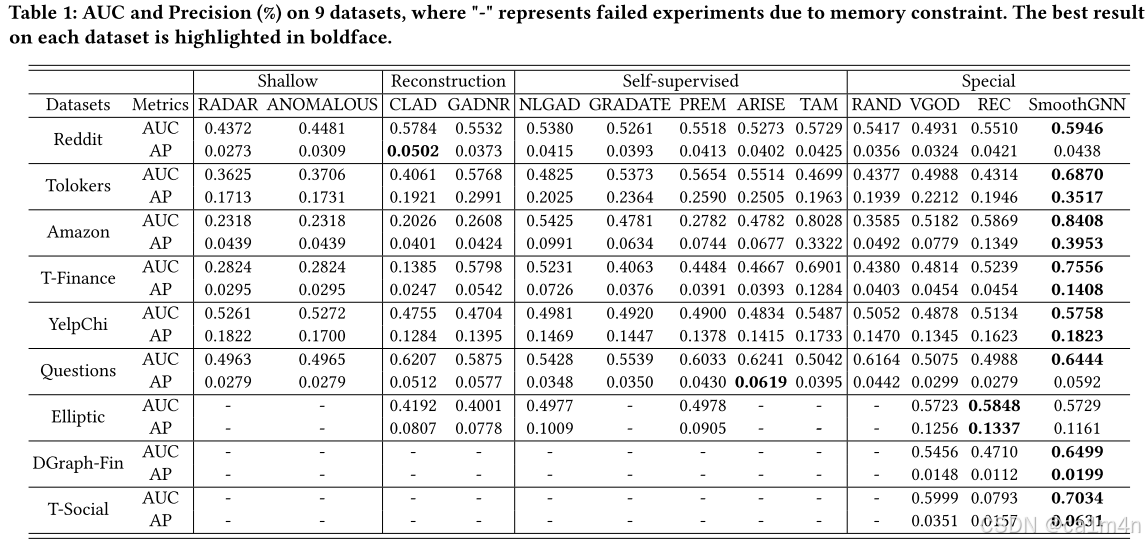
在9個真實數據集上的大量實驗表明，SmoothGNN比最佳競爭者平均高出14.66%（AUC）、7.28%（AP），運行速度提升了75倍。

開源代碼：SmoothGNN

2.2 背景與動機

節點異常檢測的常見應用場景，例如，金融網絡中的欺詐檢測、社交網絡中的惡意評論檢測、芯片制造中的熱點檢測。

在芯片制造中，Hotspot Detection（熱點檢測）是一項關鍵的質量控制技術，主要用于識別設計或制造過程中可能導致芯片缺陷的潛在問題區域。這些“熱點”通常指設計中容易在光刻、蝕刻或其他工藝步驟中出現故障的局部圖案（如短路、斷路或可靠性問題），可能影響芯片的性能或良率。
即，工業制造中的缺陷檢測

復雜的信息和大規模的現實世界的圖對如何有效與高效地檢測異常節點提出了挑戰，特別是在無監督的設置下。現有方法：淺層模型由于手工規則而表現力有限，重建模型和子監督模型計算復雜度高，特殊模型民林尋找NAD有效標識符的挑戰。

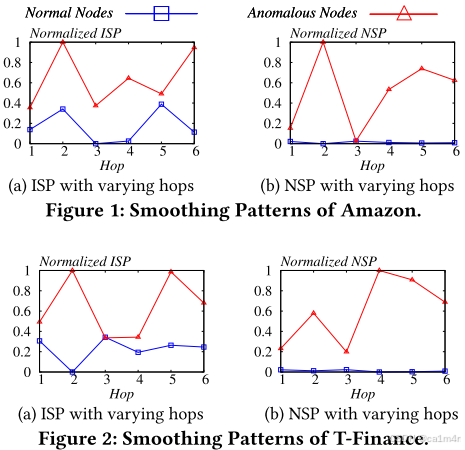
為了解決以上局限性，我們重新評估了NAD任務的傳播過程，發現平滑（Smothing）問題可以為檢測圖中的異常提供潛在優勢。具體來說，我們設計了兩個新的衡量標準：ISP和NSP，從不同角度分析平滑問題。對于ISP，我們計算在每個傳播跳的節點表示和收斂表示后獲得的異常和正常節點的無限數量的跳數之間的平均歸一化距離。對于NSP，我們分別計算異常和正常節點鄰域內的平均歸一化相似度。值得注意的是，這兩種平滑模式在現實世界的數據集中（如Amazon和T-Finance）的不同類型的節點上表現出不同的行為，分別如圖1和圖2所示。在傳播過程中，異常節點的平滑模式一般超過正常節點在大多數跳數。這一觀察結果提供了一個潛在的指標，用于評估節點的異常分數：平滑模式越高，節點越有可能是異常的。

2.3 平滑模式的分析

預備知識

譜GNN圖卷積運算可以通過Laplacians的第T階多項式來近似： $$\mathbf{U}{g}_{\theta }{\mathbf{U}}^T\mathbf{x}\approx \mathbf{U}(\sum _{t=0}^T{\theta }_t{\Lambda }^t){\mathbf{U}}^T\mathbf{x}=(\sum _{t=0}^T{\theta }_t{\mathbf{L}}^t)\mathbf{x}，$$ 其中，$\theta \in {\mathbb{R}}^{T+1}$是多項式系數。

如Figure2所討論的，每個傳播跳處的節點表示與在無限跳數之后獲得的收斂表示之間的距離對于異常節點和正常節點表現出不同的模式。
ISP：
$$I(\mathbf{x})=||(P^t?P^{\infty })x|{|}_2^2,$$其中，$P^t$是在傳播的第$t$跳之后的傳播矩陣，$P^{\infty }$是收斂狀態，$x$是圖信號。如定義所示，ISP有效地描述了傳播過程中每個獨立節點的平滑模式，它可以捕獲光譜信息和平滑模式。

NSP：$$N(x^t)=\sum _{i,j=1}^n{a}_{i,j}||\frac{x_i^t}{\sqrt{d_i+1}}?\frac{x_j^t}{\sqrt{d_j+1}}|{|}_2^2,$$
其中，$a_{i,j}$表示鄰接矩陣$\tilde{A}$的第$(i,j)$項，$d_i$是節點$i$的度，并且$x^t=P^{t}x$。NSP測量相鄰節點之間的相似性，指示在傳播期間鄰域內的平滑模式，NSP與譜空間具有很強的相關性，可以作為節點表示的系數。

我們還可以觀察到，在所有層上應用NSP可以在某些數據集上提高性能，但并不是在所有數據集上都是如此。這樣的結果證明了NSP的有效性，因為僅將其應用于最后一層或所有層都明顯優于基線。因此，為了保持模型的簡單性和穩定性，我們只將NSP應用于最后一層。