.線段樹介紹

$線段樹(SegmentTree)$ is 用于高效處理區間查詢和單點修改的數據結構，和樹狀數組很像，不知道什么是樹狀數組？看這個樹狀數組入門。
( 需要說明，區間查詢可以是不同的操作。假設區間$[L,R]$。那么查詢操作包括但不限于：區間最大值，最小值，區間和等等。后續做題如果遇到更多的操作，將會在此處補充。)

---

.線段樹框架

\;\;\;\;\;\;\;\;大致分為四個內容

---

.理解線段樹

\;\;\;\;\;\;\;\;線段樹的本質是分而治之，并且對于維護每個區間。
\;\;\;\;\;\;\;\;老規矩，先拋出一個問題，然后嘗試解決這個問題。最后優化的時候就會解釋線段樹的用處是什么。

QuesTion

給你兩個長度為 n 的整數數組，fruits 和 baskets，其中 fruits[i] 表示第 i 種水果的 數量，baskets[j]表示第 j 個籃子的容量。

你需要對 fruits 數組從左到右按照以下規則放置水果：

1. 每種水果必須放入第一個容量大于等于該水果數量的最左側可用籃子中。
2. 每個籃子只能裝一種水果。如果一種水果無法放入任何籃子，它將保持未放置。返回所有可能分配完成后，剩余未放置的水果種類的數量。

（這個問題就是leettcode的.3479）
暴力：
\;\;\;\;\;\;\;\;如果按照暴力的做法。依此遍歷$fruits$數組，對每一個$fruits[i]$，從頭到尾遍歷$baskets$數組，找到第一個大于等于$fruits[i]$的值。每一次查找的復雜度是$O(n)$,所以總體復雜度是$O(n^2)$，因此總體時間復雜度是$O(n?lo{g}_2^n)$

線段樹優化：
\;\;\;\;\;\;\;\;線段樹通過 “分治 + 區間預存” 實現高效操作。本質上是空間換時間。通過開辟新的數組構建二叉樹來存儲原數組的區間最值。二叉樹每個節點都表示其左右孩子節點的最值。這樣只需要一直往樹的孩子節點搜索，就可以找到第一個大于等于$fruits[i]$的節點值，因為二叉樹的結構，查找一個節點的時間復雜度是$O(lo{g}_2^n)$

---

.圖式整個過程

用上面Question的示例：
下面來用簡單的示例和圖來解釋：將basket數組作為葉子節點構建線段樹。每個節點存儲其子樹的節點最大值。(可以根據題目需求修改)

假設F (fruits)數組{3，1，5，2，6，4}{\{3 ，1 ，5，2 ，6，4}\}{3，1，5，2，6，4}
并且B（basket）數組{3,5,2,4,6,2,7}{\{ 3, 5, 2,4,6,2,7\}}{3,5,2,4,6,2,7}

1.建樹，葉子節點就是B數組(整個二叉樹需要建立多少個節點，下面會說的）

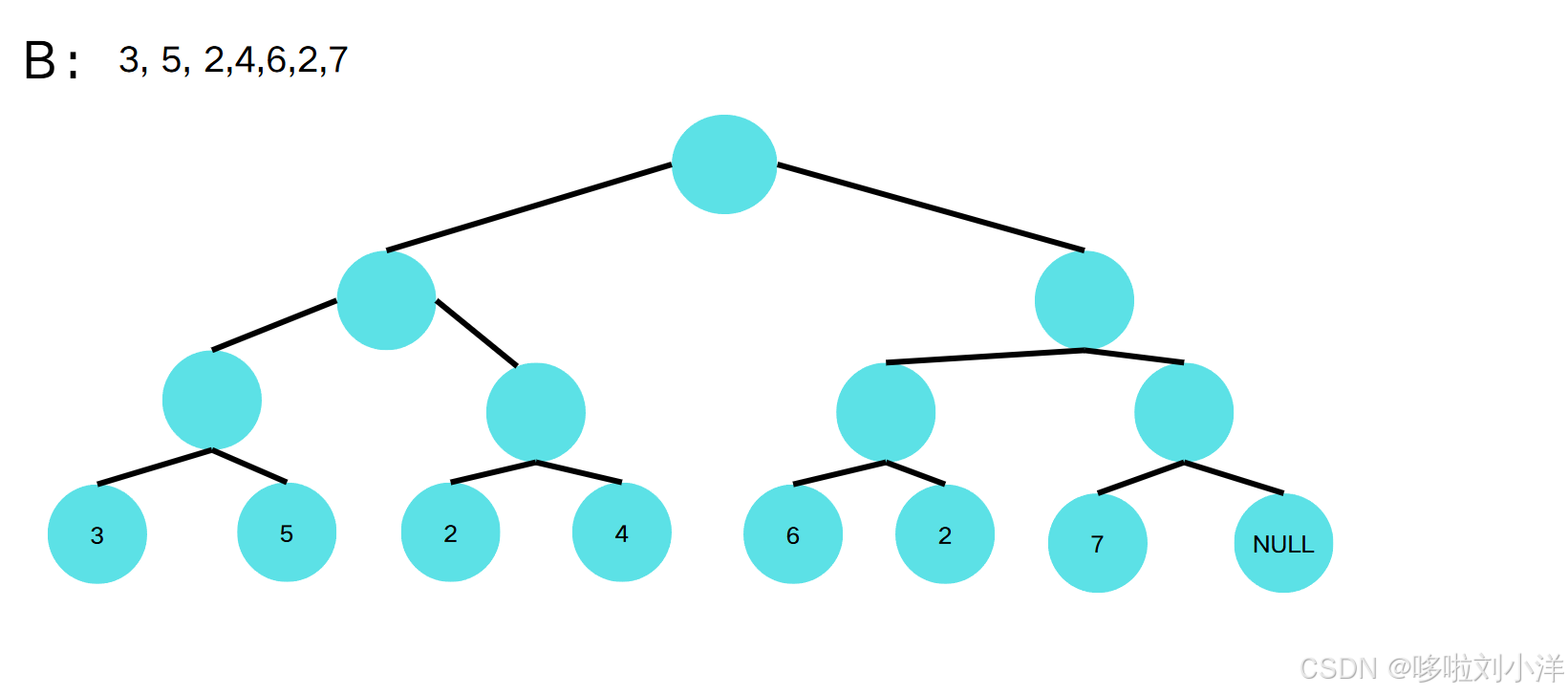
2.初始化線段樹，維護節點信息（當前節點表示當前區間的最大值）

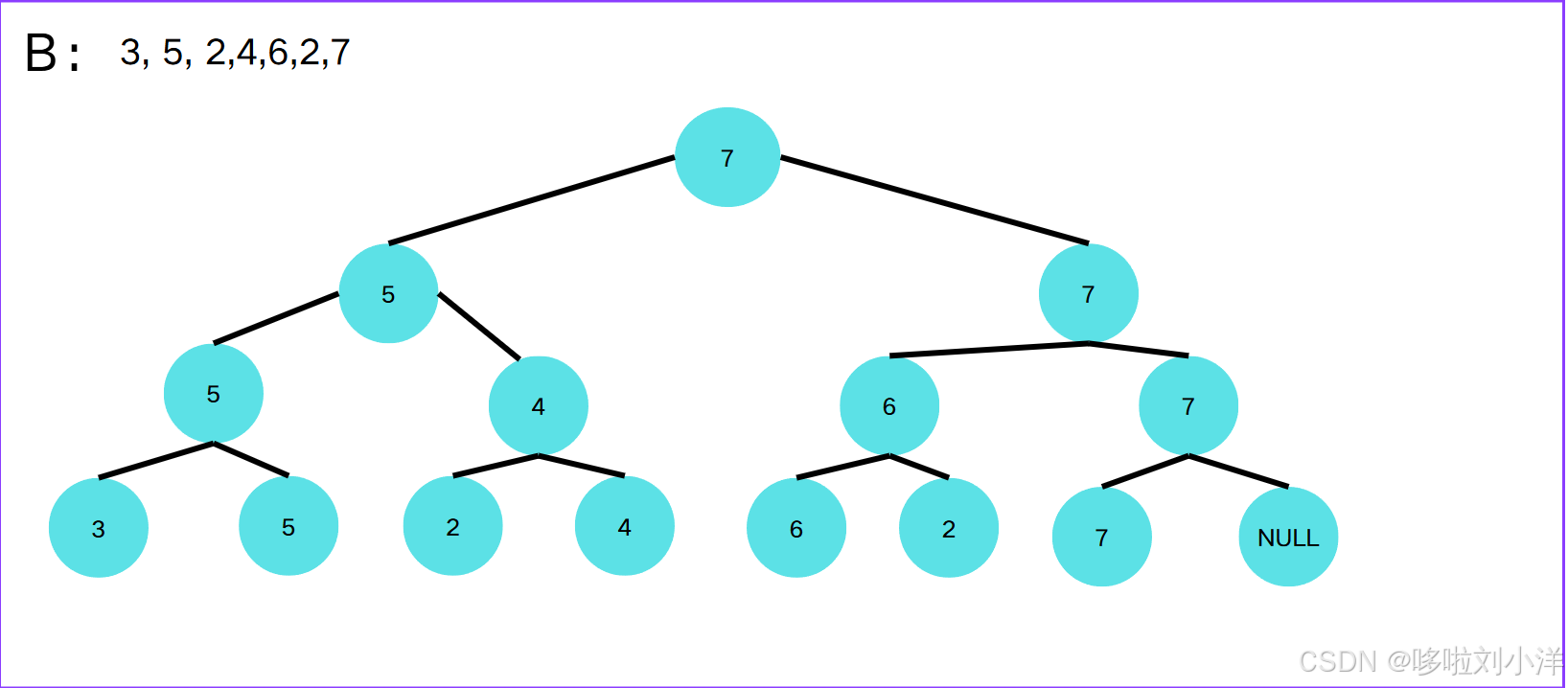
3.查詢（看出線段樹高效率的核心步驟）
對于F 數組{3，1，5，2，6，4}{\{3 ，1 ，5，2 ，6，4}\}{3，1，5，2，6，4}

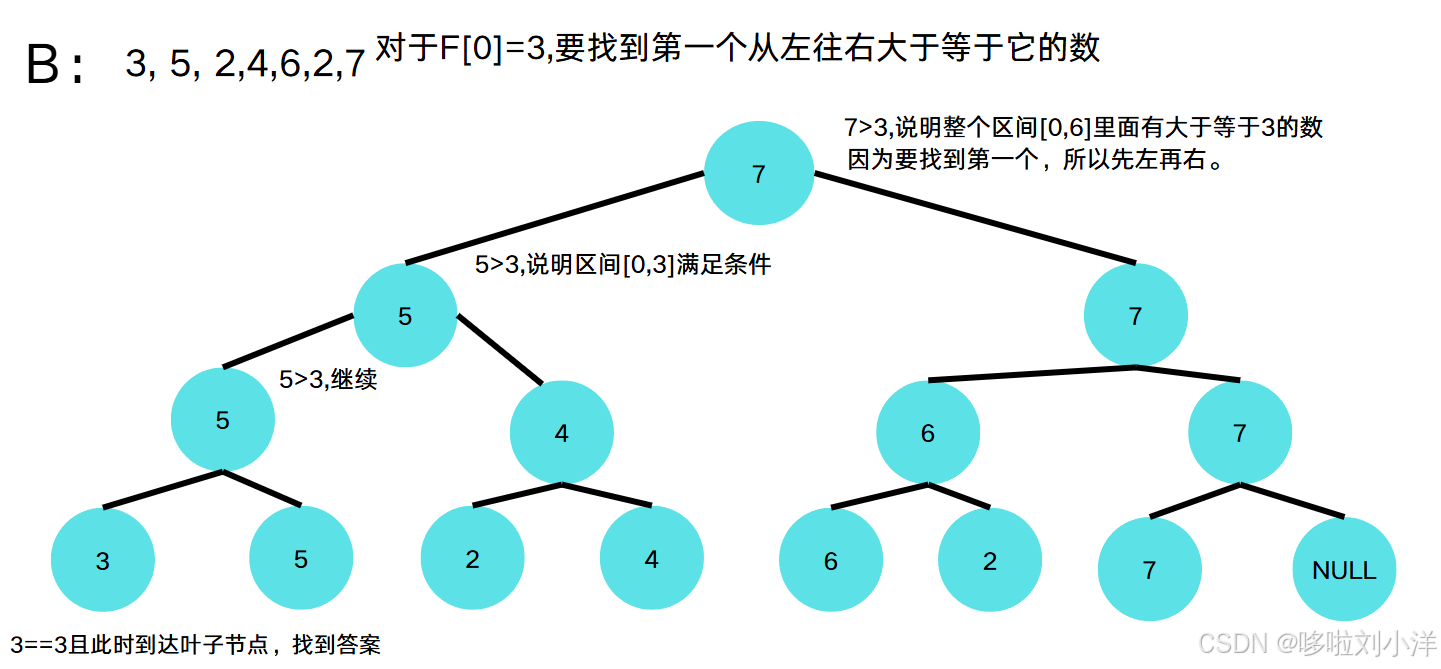
依此類推，顯然，每次查詢，遇到大于等于x的就往下走，否則往上走，這樣查詢一次做多尋找Logn次。這個例子只是明了知道線段樹的分而治之這個特點，實際上具體例子具體分析，但是都離不開分而治之這四個字。

.線段樹代碼逐層解析

線段樹私有成員變量

class SegmentTree
{
private:int n;   //線段樹一共n個節點空間，但不一定用到n個vector<int>tree;
}

更新操作節點最大值

int mergeLR(int& a,int& b)
{	return max(a,b);  //根據題目改
}
void maintain(int idx) //更新當前節點的最大值(也就是左右孩子節點的最大值）
{tree[idx]=mergeLR(tree[idx*2],tree[idx*2+1]);
}

建樹

//idx表示當前節點，[l,r]表示當前建樹的區間,當然，idx在[l,r]內
void built(vector<int>&a,int idx,int l,int r) 
{if(l==r)  //當是葉子節點的時候，說明當前位置就是放置元素的位置。{	tree[idx]=a[l];return;}int m=(l+r)>>1;bilut(a,idx*2,l,m);   // 遞歸初始化左子樹built(a,idx*2+1,m+1,r);   //遞歸初始化右子樹maintain(idx);  //更新當前的節點值,發現，節點值的更新是后續遍歷
}

修改值(也叫更新，但是這個更新是查找+更新）

//線段樹下標i的值修改為val
void update(int idx,int l,int r,int i,int val)
{if(l==r}  //到葉子節點說明找到了{tree[idx]=mergeLR(tree[idx],val);return;}int m=(l+r)/2;if(i<=m)   //在左子樹{update(idx*2,l,m,i,val);}else   //在右子樹{update(idx*2+1,m+1,r,i,val);}maintain(idx);  //更新完左右子樹，更新當前節點
}

查詢區間[ql,qr]最大值

int query(int idx,int l,int r,int ql,int qr)const
{if(ql<=l&&r<=qr)// 當前子樹完全在 [ql, qr] 內return tree[idx];int m=(l+r)>>1;if(qr<=m)   //[ql,qr]完全在左子樹return query(idx*2,l,m,ql,qr);if(qr>m)   //[ql,qr]完全在右子樹return query(idx*2+1,m+1,r,ql,qr);//否則[ql,qr]在左右子樹各有部分int l_res=query(idx*2,l,m,ql,m);int r_res=query(idx*2+1,m+1,r,m+1,qr);return mergeLR(l_res,r_res);  //合并左右子樹
}

構造函數初始化

// 線段樹維護一個長為 n 的數組（下標從 0 到 n-1），元素初始值為 init_val
SegmentTree((int n,int init_val):SegmentTree(vector<int>(n,init_val)){}// 線段樹維護數組 a
SegmentTree(const vector<int>& a) : n(a.size()), tree(2 << bit_width(a.size() - 1)) {build(a, 1, 0, n - 1);
}

線段樹為什么要開辟2 << bit_width(a.size() - 1)個元素空間？

---

.代碼匯總

和上面略有不同，這是靈神的代碼，邏輯是一樣的。代碼來源

// 線段樹有兩個下標，一個是線段樹節點的下標，另一個是線段樹維護的區間的下標
// 節點的下標：從 1 開始，如果你想改成從 0 開始，需要把左右兒子下標分別改成 node*2+1 和 node*2+2
// 區間的下標：從 0 開始
template<typename T>
class SegmentTree 
{// 注：也可以去掉 template<typename T>，改在這里定義 T// using T = pair<int, int>;int n;vector<T> tree;// 合并兩個 valT merge_val(T a, T b) const {return max(a, b); // **根據題目修改**}// 合并左右兒子的 val 到當前節點的 valvoid maintain(int node) {tree[node] = merge_val(tree[node * 2], tree[node * 2 + 1]);}// 用 a 初始化線段樹// 時間復雜度 O(n)void build(const vector<T>& a, int node, int l, int r) {if (l == r) { // 葉子tree[node] = a[l]; // 初始化葉節點的值return;}int m = (l + r) / 2;build(a, node * 2, l, m); // 初始化左子樹build(a, node * 2 + 1, m + 1, r); // 初始化右子樹maintain(node);}void update(int node, int l, int r, int i, T val) {if (l == r) { // 葉子（到達目標）// 如果想直接替換的話，可以寫 tree[node] = valtree[node] = merge_val(tree[node], val);return;}int m = (l + r) / 2;if (i <= m) { // i 在左子樹update(node * 2, l, m, i, val);} else { // i 在右子樹update(node * 2 + 1, m + 1, r, i, val);}maintain(node);}T query(int node, int l, int r, int ql, int qr) const {if (ql <= l && r <= qr) { // 當前子樹完全在 [ql, qr] 內return tree[node];}int m = (l + r) / 2;if (qr <= m) { // [ql, qr] 在左子樹return query(node * 2, l, m, ql, qr);}if (ql > m) { // [ql, qr] 在右子樹return query(node * 2 + 1, m + 1, r, ql, qr);}T l_res = query(node * 2, l, m, ql, qr);T r_res = query(node * 2 + 1, m + 1, r, ql, qr);return merge_val(l_res, r_res);}
public:// 線段樹維護一個長為 n 的數組（下標從 0 到 n-1），元素初始值為 init_valSegmentTree(int n, T init_val) : SegmentTree(vector<T>(n, init_val)) {}// 線段樹維護數組 aSegmentTree(const vector<T>& a) : n(a.size()), tree(2 << bit_width(a.size() - 1)) {build(a, 1, 0, n - 1);}// 更新 a[i] 為 merge_val(a[i], val)// 時間復雜度 O(log n)void update(int i, T val) {update(1, 0, n - 1, i, val);}// 返回用 merge_val 合并所有 a[i] 的計算結果，其中 i 在閉區間 [ql, qr] 中// 時間復雜度 O(log n)T query(int ql, int qr) const {return query(1, 0, n - 1, ql, qr);}// 獲取 a[i] 的值// 時間復雜度 O(log n)T get(int i) const {return query(1, 0, n - 1, i, i);}
};int main() 
{SegmentTree t(8, 0LL); // 如果這里寫 0LL，那么 SegmentTree 存儲的就是 long long 數據t.update(0, 1LL << 60);cout << t.query(0, 7) << endl;vector<int> nums = {3, 1, 4, 1, 5, 9, 2, 6};// 注意：如果要讓 SegmentTree 存儲 long long 數據，需要傳入 vector<long long>SegmentTree t2(nums); // 這里 SegmentTree 存儲的是 int 數據cout << t2.query(0, 7) << endl;return 0;
}

.leetcode練習

2286.Booking Concert Tickets in Groups
3479.Fruits into Baskets III
2940.Find Building Where Alice and Bob Can Meet
2231.由單個字符重復的最長子字符串
題單完整見
Click here: More

對于2231.比較更具體地了解線段樹地本質，至少我是這樣認為的。