引言
當你第一次看到線性回歸時,你是否注意到了作為參數優化關鍵的損失函數(均方損失),你是否能夠理解它的本質和由來。其實,在我第一次接觸時,我是感到有些驚訝的,然后試著去強行理解它,而沒有想到它的背后其實有一個數學理論作為支撐——最大似然估計。
最大似然估計
最大似然估計(Maximum Likelihood Estimation,MLE)是一種在統計學和機器學習中用于估計模型參數的方法。其核心思想是:在已知觀測數據的情況下,尋找使得觀測數據出現概率最大的模型參數值。(核心在于概率最大)
似然函數

我們的目的就是把上面的似然函數變成最大。
下面我們將以均方損失和交叉熵損失作為案例進行說明。
均方損失(MSE):對應 “觀測噪聲服從高斯分布” 的 MLE
概率假設:模型預測誤差服從高斯分布

theta是參數,也就是均值和方差。
構建對數似然函數

最大化對數似然 → 最小化 MSE

結論
均方損失是 “假設回歸任務的觀測噪聲服從高斯分布” 時,最大似然估計的等價損失函數(即負對數似然)。
交叉熵損失:對應 “類別標簽服從伯努利 / 多項式分布” 的 MLE
交叉熵損失是分類任務(輸出為離散類別概率,如判斷圖像是貓 / 狗 / 鳥)中最常用的損失函數,分為二分類和多分類兩種形式:

以二分類為例(多分類同理,只需將伯努利分布擴展為多項式分布):
概率假設:類別標簽服從伯努利分布

這個函數設計地很巧妙。
構建對數似然函數

最大化對數似然 → 最小化交叉熵
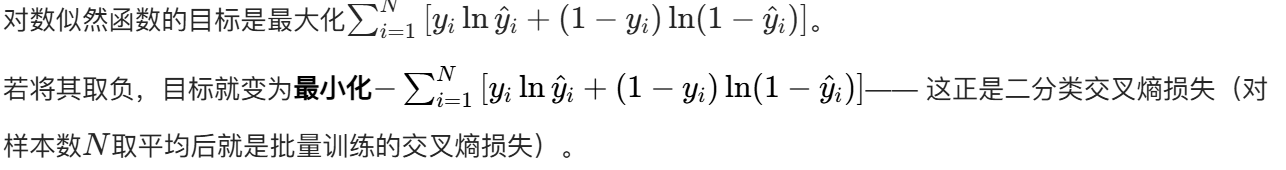
多分類的擴展

結論
交叉熵損失是 “假設分類任務的類別標簽服從伯努利分布(二分類)或多項式分布(多分類)” 時,最大似然估計的等價損失函數(即負對數似然)。
核心對比:MSE 與交叉熵的 MLE 本質差異
兩種損失函數的根本區別源于對 “標簽生成過程” 的概率假設不同,而這種假設又由任務類型(回歸 / 分類)決定:
| 損失函數 | 適用任務 | 背后的概率分布假設 | MLE 關聯(等價性) |
|---|---|---|---|
| 均方損失(MSE) | 回歸(連續輸出) | 觀測噪聲~高斯分布 | 最小化 MSE = 最大化高斯分布下的對數似然 |
| 交叉熵損失(CE) | 分類(離散類別) | 類別標簽~伯努利 / 多項式分布 | 最小化 CE = 最大化伯努利 / 多項式分布下的對數似然 |
怎么說呢?感覺還是很神奇的,損失函數竟然就這么水靈靈的被推導出來了。






(含中國電力年鑒))












)