程序詳解

概述

本代碼實現基于擴展卡爾曼濾波器（EKF）的二維組合導航系統，融合IMU（慣性測量單元）和GNSS（全球導航衛星系統）數據，實現精確的位置和速度估計。該系統采用8維誤差狀態模型，在圓形軌跡上進行仿真驗證。

系統架構

狀態向量定義

系統采用8維狀態向量：

$$\mathbf{x}=\left[\begin{array}{c}{p}_x\\ p_y\\ v_x\\ v_y\\ \psi \\ b_g\\ b_{ax}\\ b_{ay}\end{array}\right]$$

其中：

• $p_x,p_y$：X、Y方向位置 (m)
• $v_x,v_y$：X、Y方向速度 (m/s)
• $\psi$：航向角 (rad)
• $b_g$：陀螺儀偏差 (rad/s)
• $b_{ax},b_{ay}$：X、Y方向加速度計偏差 (m/s2)

觀測向量定義

觀測向量為2維GNSS位置觀測：

$$\mathbf{z}=\left[\begin{array}{c}{p}_x\\ p_y\end{array}\right]$$

核心數學模型

狀態轉移方程

系統的非線性狀態轉移方程為：

$${\mathbf{x}}_{k+1}=f({\mathbf{x}}_k,{\mathbf{u}}_k,{\mathbf{w}}_k)$$

具體形式：

$$\begin{array}{rl}{p}_{x,k+1}& =p_{x,k}+v_{x,k}?\Delta t\\ p_{y,k+1}& =p_{y,k}+v_{y,k}?\Delta t\\ v_{x,k+1}& =v_{x,k}+(f_{x,k}?b_{ax,k})\cos {\psi }_k?(f_{y,k}?b_{ay,k})\sin {\psi }_k?\Delta t\\ v_{y,k+1}& =v_{y,k}+(f_{x,k}?b_{ax,k})\sin {\psi }_k+(f_{y,k}?b_{ay,k})\cos {\psi }_k?\Delta t\\ {\psi }_{k+1}& ={\psi }_k+({\omega }_k?b_{g,k})?\Delta t\\ b_{g,k+1}& =b_{g,k}\\ b_{ax,k+1}& =b_{ax,k}\\ b_{ay,k+1}& =b_{ay,k}\end{array}$$

其中：

• $f_{x,k},f_{y,k}$：IMU測量的比力 (m/s2)
• ${\omega }_k$：IMU測量的角速度 (rad/s)
• $\Delta t$：采樣時間間隔

狀態轉移雅可比矩陣

EKF需要計算狀態轉移函數的雅可比矩陣 $\mathbf{F}$：

$$\mathbf{F}=\frac{?f}{?\mathbf{x}}{|}_{{\mathbf{x}}_{k|k?1}}$$

主要的非零元素包括：

$$\begin{array}{rl}{F}_{1,3}& =F_{2,4}=\Delta t\\ F_{3,5}& =?(f_x?b_{ax})\sin \psi ?(f_y?b_{ay})\cos \psi ?\Delta t\\ F_{4,5}& =(f_x?b_{ax})\cos \psi ?(f_y?b_{ay})\sin \psi ?\Delta t\\ F_{3,7}& =F_{4,8}=?\cos \psi ?\Delta t\\ F_{3,8}& =F_{4,7}=\sin \psi ?\Delta t\\ F_{5,6}& =?\Delta t\end{array}$$

觀測方程

觀測方程為線性的：

$${\mathbf{z}}_k=\mathbf{H}{\mathbf{x}}_k+{\mathbf{v}}_k$$

觀測雅可比矩陣 $\mathbf{H}$ 為：

$$\mathbf{H}=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\end{array}\right]$$

噪聲模型

過程噪聲協方差矩陣Q：

$$\mathbf{Q}=\text{diag}\left[\begin{array}{c}({\sigma }_a\Delta t^2{)}^2{\mathbf{I}}_{2\times 2}\\ ({\sigma }_a\Delta t{)}^2{\mathbf{I}}_{2\times 2}\\ ({\sigma }_{\omega }\Delta t{)}^2\\ ({\sigma }_{bg}\Delta t{)}^2\\ ({\sigma }_{ba}\Delta t{)}^2{\mathbf{I}}_{2\times 2}\end{array}\right]$$

其中：

• ${\sigma }_a=0.01$ m/s2：加速度計噪聲標準差
• ${\sigma }_{\omega }=0.1°$ = 0.0017 rad/s：陀螺儀噪聲標準差
• ${\sigma }_{bg}=0.01°$ = 0.00017 rad/s：陀螺儀偏差噪聲標準差
• ${\sigma }_{ba}=0.001$ m/s2：加速度計偏差噪聲標準差

觀測噪聲協方差矩陣R：

$$\mathbf{R}={\sigma }_{gnss}^2{\mathbf{I}}_{2\times 2}$$

其中 ${\sigma }_{gnss}=3$ m：GNSS位置觀測噪聲標準差

性能評估

系統通過以下指標評估濾波性能：

1. 位置均方根誤差（RMSE）：
   $${\text{RMSE}}_{pos}=\sqrt{\frac{1}{N}\sum _{k=1}^N[(p_{x,k}^{est}?p_{x,k}^{true}{)}^2+(p_{y,k}^{est}?p_{y,k}^{true}{)}^2]}$$

2. 速度均方根誤差（RMSE）：
   $${\text{RMSE}}_{vel}=\sqrt{\frac{1}{N}\sum _{k=1}^N[(v_{x,k}^{est}?v_{x,k}^{true}{)}^2+(v_{y,k}^{est}?v_{y,k}^{true}{)}^2]}$$

算法特點

1. 多傳感器融合：有效融合高頻IMU數據和低頻GNSS觀測
2. 偏差估計：實時估計并補償陀螺儀和加速度計偏差
3. 誤差狀態建模：采用誤差狀態方法提高線性化精度
4. 實時性能：適合在線實時導航應用

該EKF組合導航算法在保持計算效率的同時，顯著提高了導航精度，特別是在GNSS信號中斷期間仍能保持較好的位置估計性能。

運行結果

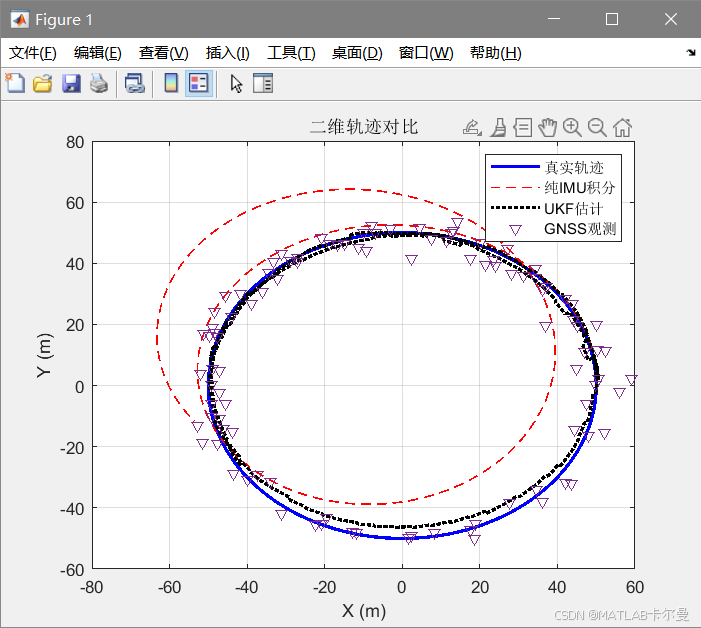
軌跡對比：

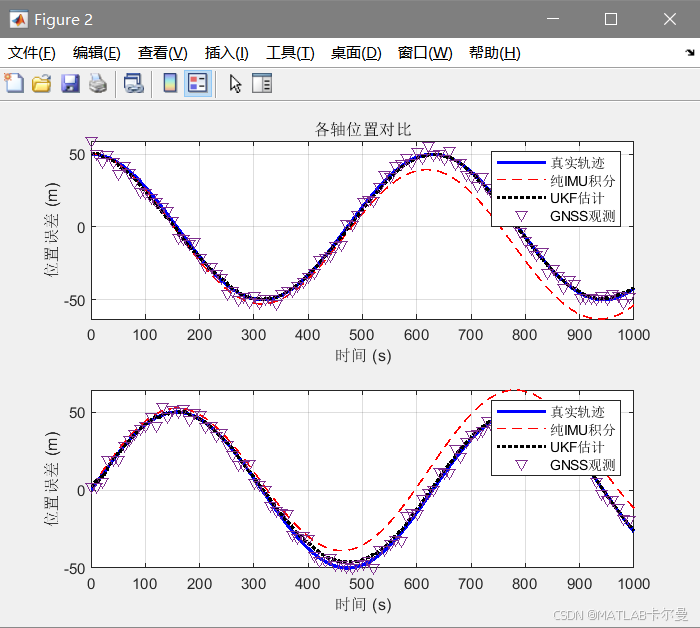
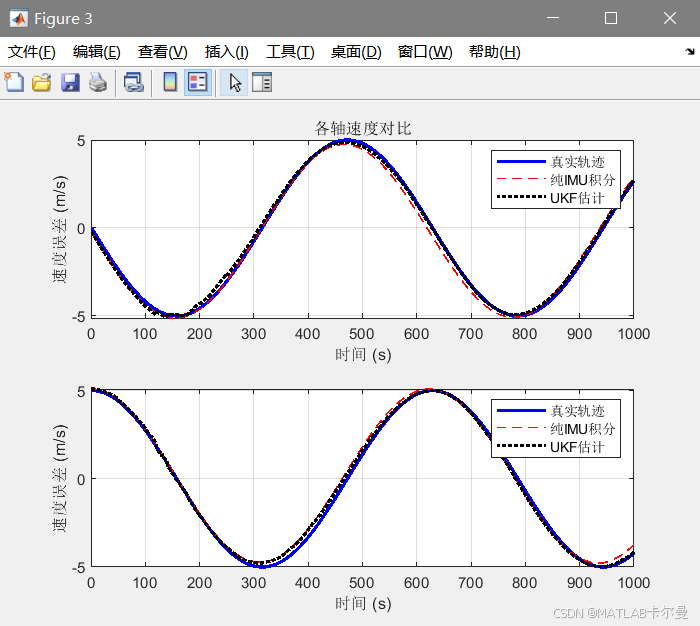
各軸位移與速度曲線對比：

誤差對比：

命令行截圖：

MATLAB源代碼

部分代碼如下：

% 二維狀態量的EKF例程（有嚴格的組合導航推導）
% 基于8維誤差狀態模型：位置、速度、航向、航向角角速度偏差、加速度計偏差
% 基于2維的觀測模型：XY兩個軸的位置
% 作者：matlabfilter
% 2025-08-27/Ver1clear; clc; close all;
rng(0); % 固定隨機種子%% 系統參數設置
dt = 0.1;           % 采樣時間間隔 (s)
total_time = 100;   % 總仿真時間 (s)
N = total_time / dt; % 采樣點數%% 噪聲參數設置
% IMU噪聲參數
gyro_noise_std = 0.1 * pi/180;      % 陀螺噪聲標準差 (rad/s)
accel_noise_std = 0.01;             % 加速度計噪聲標準差 (m/s^2)
gyro_bias_std = 0.01 * pi/180;      % 陀螺偏差標準差 (rad/s)
accel_bias_std = 0.001;             % 加速度計偏差標準差 (m/s^2)% GNSS觀測噪聲
gnss_pos_noise_std = 3;             % GNSS位置噪聲標準差 (m)%% 過程噪聲協方差矩陣Q (8×8)
% 狀態順序：[位置(2), 速度(2), 航向角(1), 航向角角速度偏差(1), 加速度計偏差(2)]
Q = zeros(8, 8);
% 位置噪聲（通過速度積分產生）
Q(1:2, 1:2) = eye(2) * (accel_noise_std * dt^2)^2;
% 速度噪聲
Q(3:4, 3:4) = eye(2) * (accel_noise_std * dt)^2;
% 姿態噪聲
Q(5, 5) = eye(1) * (gyro_noise_std * dt)^2;
% 陀螺偏差噪聲
Q(6, 6) = eye(1) * (gyro_bias_std * dt)^2;
% 加速度計偏差噪聲
Q(7:8, 7:8) = eye(2) * (accel_bias_std * dt)^2;

代碼下載鏈接：
https://download.csdn.net/download/callmeup/91800451

如需幫助，或有導航、定位濾波相關的代碼定制需求，請點擊下方卡片聯系作者