一、搜索

1. 什么是搜索？

搜索，是一種枚舉，通過窮舉所有的情況來找到最優解，或者統計合法解的個數。因此，搜索有時候也叫作暴搜。 搜索一般分為深度優先搜索 (DFS) 與寬度優先搜索 (BFS) 。

2. 遍歷 vs 搜索

深度優先遍歷 vs 深度優先搜索，寬度優先遍歷 vs 寬度優先搜索？遍歷是形式，搜索是目的。 不過，在一般情況下，我們不會去糾結概念的差異，兩者可以等同。

3. 回溯與剪枝

回溯：當在搜索的過程中，遇到走不通或者走到底的情況時，就回頭。

剪枝：剪掉在搜索過程中，重復出現或者不是最優解的分支。

---

二、OJ 練習

1. 枚舉子集 ?

【題目鏈接】

B3622 枚舉子集（遞歸實現指數型枚舉） - 洛谷

【題目描述】

今有 $n$ 位同學，可以從中選出任意名同學參加合唱。

請輸出所有可能的選擇方案。

【輸入格式】

僅一行，一個正整數 $n$。

【輸出格式】

若干行，每行表示一個選擇方案。

每一種選擇方案用一個字符串表示，其中第 $i$ 位為 Y 則表示第 $i$ 名同學參加合唱；為 N 則表示不參加。

需要以字典序輸出答案。

【示例一】

輸入

3

輸出

NNN
NNY
NYN
NYY
YNN
YNY
YYN
YYY

【說明/提示】

對于 $100\%$ 的數據，保證 $1\le n\le 10$。

---

(1) 解題思路

對于題目中給的示例來說，我們一共有 3 個人，也就是說我們有三個字母需要填，那么對于每一個字母都有兩種情況，我們不妨畫出一個樹狀圖來展示枚舉的過程。

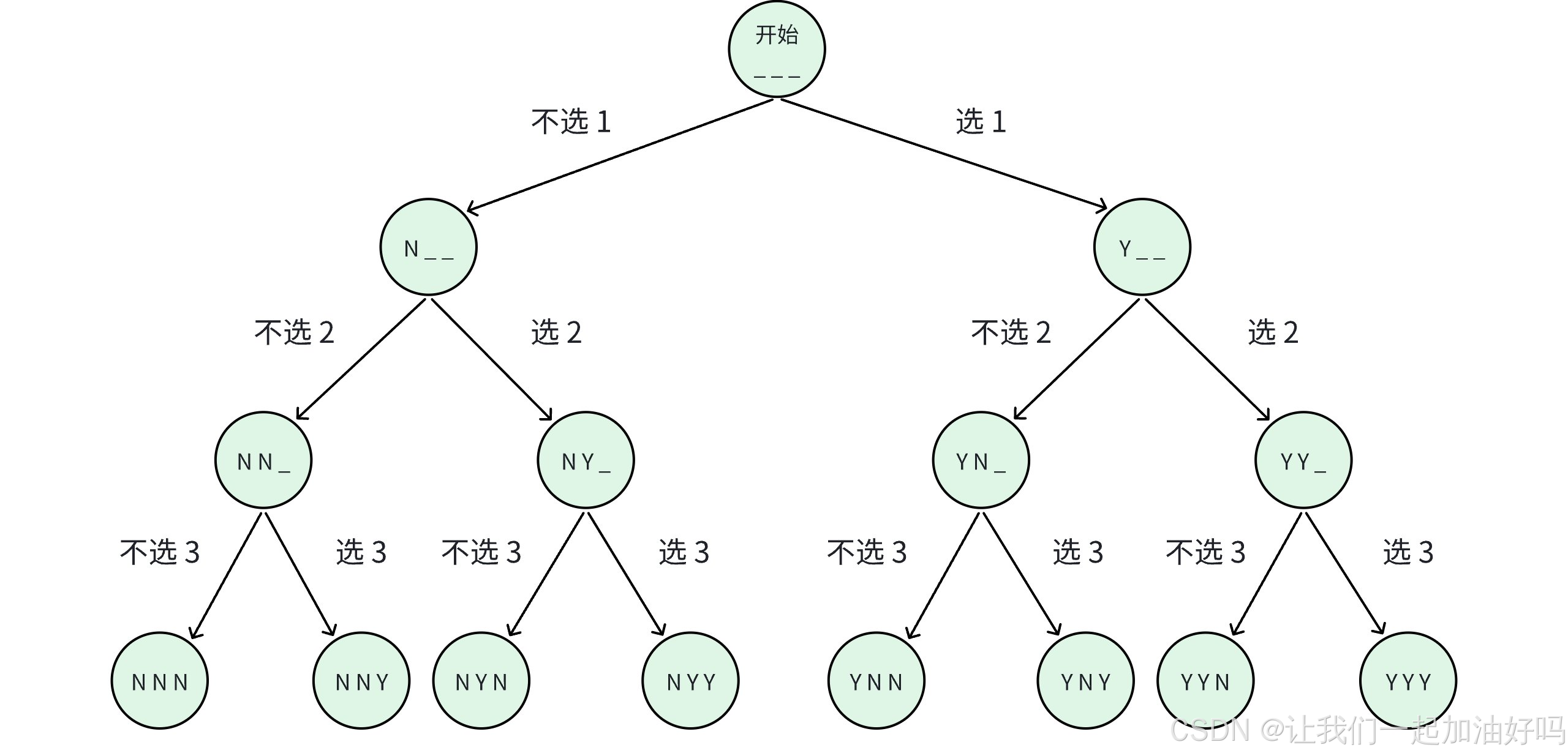
這樣的一棵樹狀圖又可以被稱為決策樹，它能夠很好的幫助我們枚舉出最后的答案，我們想要獲取答案實質上就是對這一棵樹進行一次深度優先遍歷 (DFS) 。

接下來我們只需要模擬一遍這個決策樹的過程即可。怎么模擬？首先，我們肯定是需要用到遞歸函數的，那么遞歸函數內部該如何設計？這就要看我們的決策樹了。函數體的主體部分就是在模擬決策樹的每一層都干了些什么，結束條件就是到葉子節點的時候。

---

(2) 代碼實現

#include<iostream>using namespace std;string path;  // 記錄遞歸過程中，每一步的決策
int n;void dfs()
{if(path.size() == n)  // 如果大小為n了說明到葉子節點了，需要輸出{cout << path << endl;return;}// 不選path += 'N';dfs();  // 遞歸到決策樹下一層// 到這里就已經重新回到上一層了，這個時候 path 內的最后一個位置還保留了下面層的數據，需要清除掉path.pop_back();  // 回溯，恢復現場// 選path += 'Y';dfs();  // 遞歸到下一層path.pop_back();  // 回溯，恢復現場
}int main()
{cin >> n;dfs();return 0;
}

---

2. 組合型枚舉 ?

P10448 組合型枚舉 - 洛谷

【題目描述】

從 $1～n$ 這 $n$ 個整數中隨機選出 $m$ 個，輸出所有可能的選擇方案。

【輸入格式】

兩個整數 $n,m$ ,在同一行用空格隔開。

【輸出格式】

按照從小到大的順序輸出所有方案，每行 $1$ 個。

首先，同一行內的數升序排列，相鄰兩個數用一個空格隔開。

其次，對于兩個不同的行，對應下標的數一一比較，字典序較小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

【示例一】

輸入

5 3

輸出

1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5

【說明/提示】

對于所有測試數據滿足 $0\le m\le n$ , $ n+(n-m) \le 25 $。

---

(1) 解題思路

首先畫出決策樹：

注意到在這道題中，由于我們需要枚舉的是升序的序列，每一層枚舉的時候是從前一個位置數字的下一個數字開始枚舉的，因此在 dfs() 函數中，我們需要知道當前層我們應該從哪里開始枚舉。

(2) 代碼實現

#include<iostream>
#include<vector>using namespace std;vector<int> path;  // 記錄遞歸過程
int n, m;// 從 begin 位置開始往后枚舉
void dfs(int begin)
{if(path.size() == m)  // 結束條件{for(auto e : path) cout << e << " ";cout << endl;return;}for(int i = begin; i <= n; i++){path.push_back(i); dfs(i + 1);  // 下一層就從當前位置填的這個數的下一個數開始枚舉path.pop_back();  // 恢復現場}
}int main()
{cin >> n >> m;dfs(1);return 0;
}

---

3. 枚舉排列 ?

【題目鏈接】

B3623 枚舉排列（遞歸實現排列型枚舉） - 洛谷

【題目描述】

今有 $n$ 名學生，要從中選出 $k$ 人排成一列拍照。

請按字典序輸出所有可能的排列方式。

【輸入格式】

僅一行，兩個正整數 $n,k$。

【輸出格式】

若干行，每行 $k$ 個正整數，表示一種可能的隊伍順序。

【示例一】

輸入

3 2

輸出

1 2
1 3
2 1
2 3
3 1
3 2

【說明/提示】

對于 $100\%$ 的數據，$1\le k\le n\le 10$。

---

(1) 解題思路

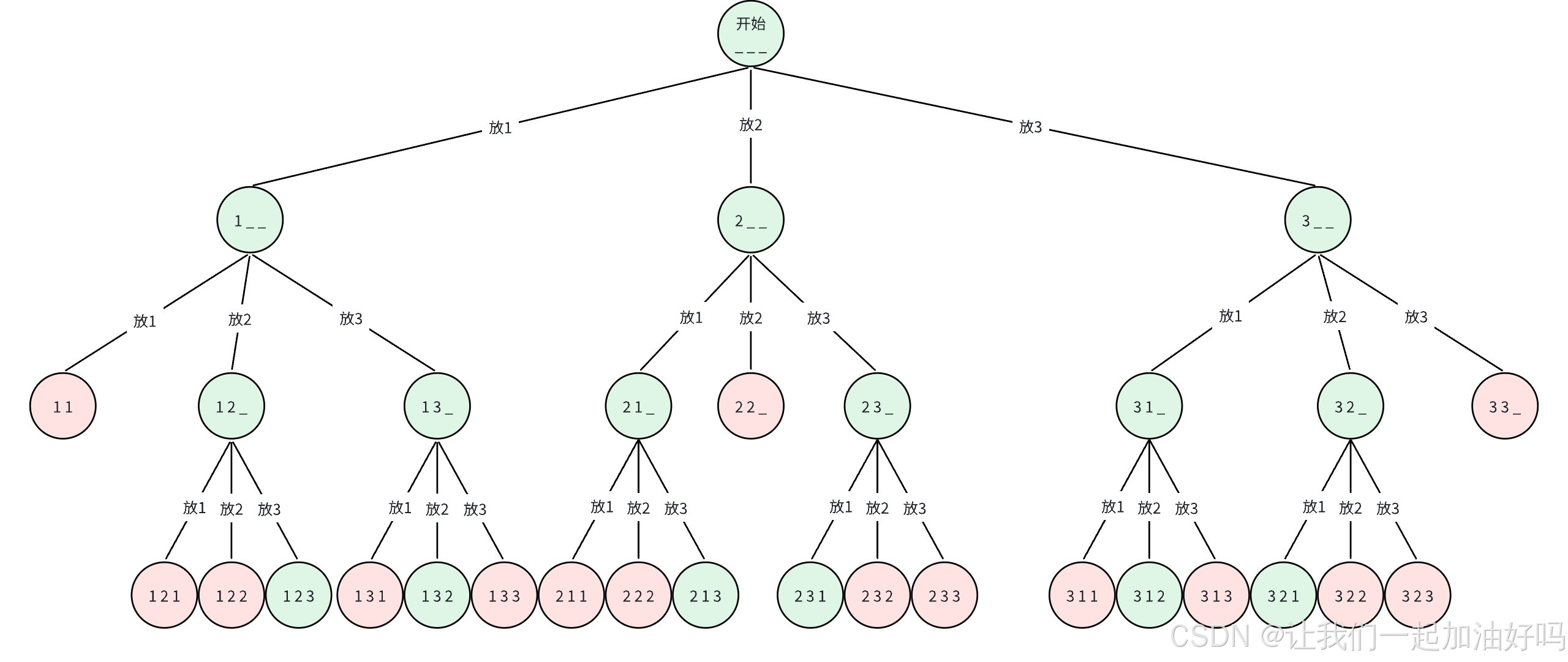
首先畫出決策樹：

遞歸函數主體部分的邏輯就是在枚舉 1, 2, 3 這三個數，所以我們只需要寫一個 for 循環枚舉 1 ~ n 即可。重點是我們不能選擇已經選過的數字，也就是說我們需要剪枝。如何實現剪枝呢？我們可以搞一個 vis 數組，它的第 i 個位置代表 i 這個數有沒有被選擇過，在我們枚舉的過程中只需要在 vis 數組中看一下當前位置的是否被選擇過即可，如果被選擇過那么 continue，否則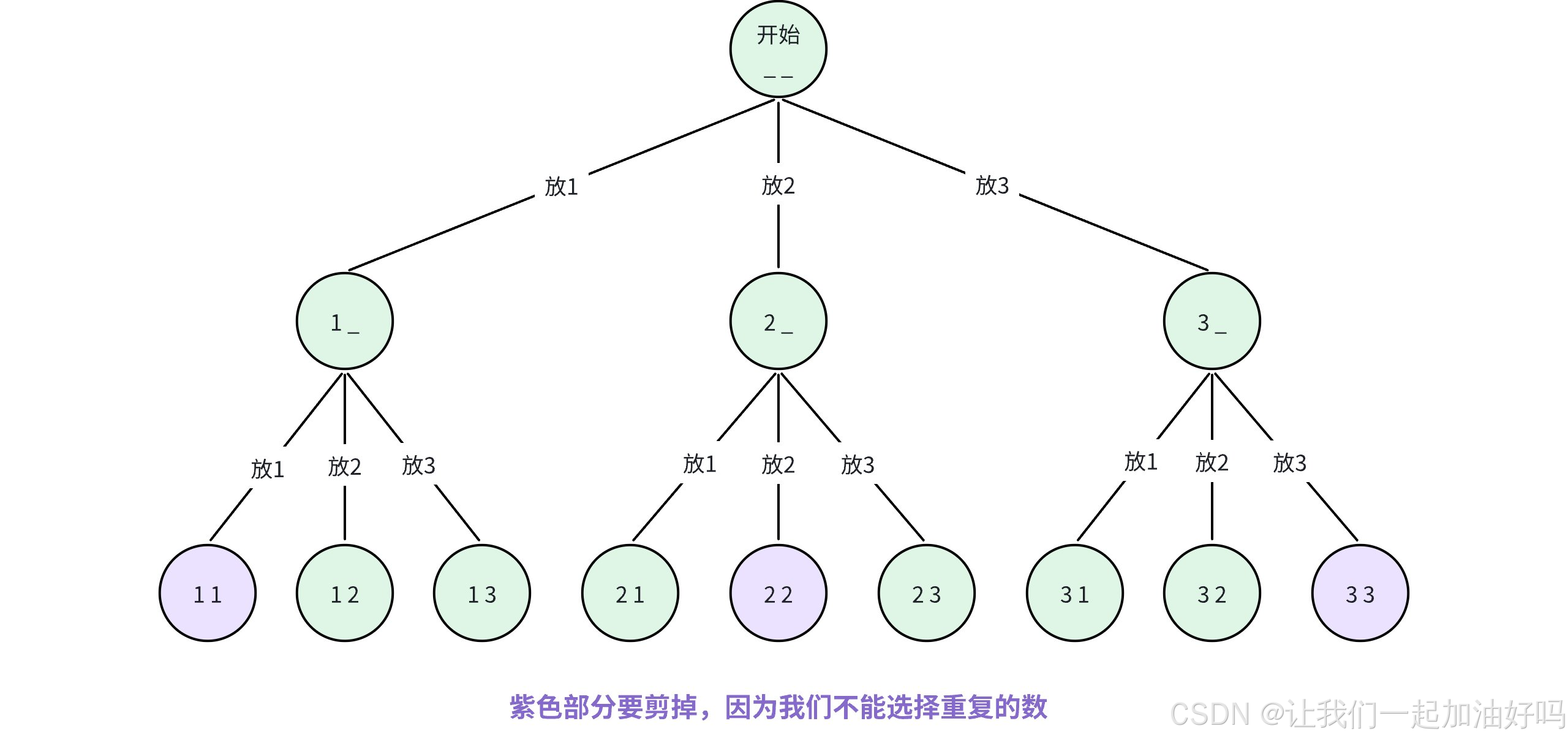
就正常執行。

---

(2) 代碼實現

#include<iostream>
#include<vector>using namespace std;const int N = 15;vector<int> path;
bool vis[N];  // 標記哪些數已經被選擇了
int n, m;void dfs()
{if(path.size() == m){for(auto e : path) cout << e << " ";cout << endl;return;}for(int i = 1; i <= n; i++){if(!vis[i])  // 如果當前數沒有被選擇{path.push_back(i);vis[i] = true;  // 當前數被選擇了，需要在 vis 數組中標記一下dfs();  // 遞歸到下一層path.pop_back();  // 恢復現場vis[i] = false;  // 恢復現場}}
}int main()
{cin >> n >> m;dfs();return 0;
}

---

4. 全排列問題 ?

【題目鏈接】

P1706 全排列問題 - 洛谷

【題目描述】

按照字典序輸出自然數 $1$ 到 $n$ 所有不重復的排列，即 $n$ 的全排列，要求所產生的任一數字序列中不允許出現重復的數字。

【輸入格式】

一個整數 $n$。

【輸出格式】

由 $1～n$ 組成的所有不重復的數字序列，每行一個序列。

每個數字保留 $5$ 個場寬。

【示例一】

輸入

3

輸出

	1    2    31    3    22    1    32    3    13    1    23    2    1

【說明/提示】

$1\le n\le 9$。

---

(1) 解題思路

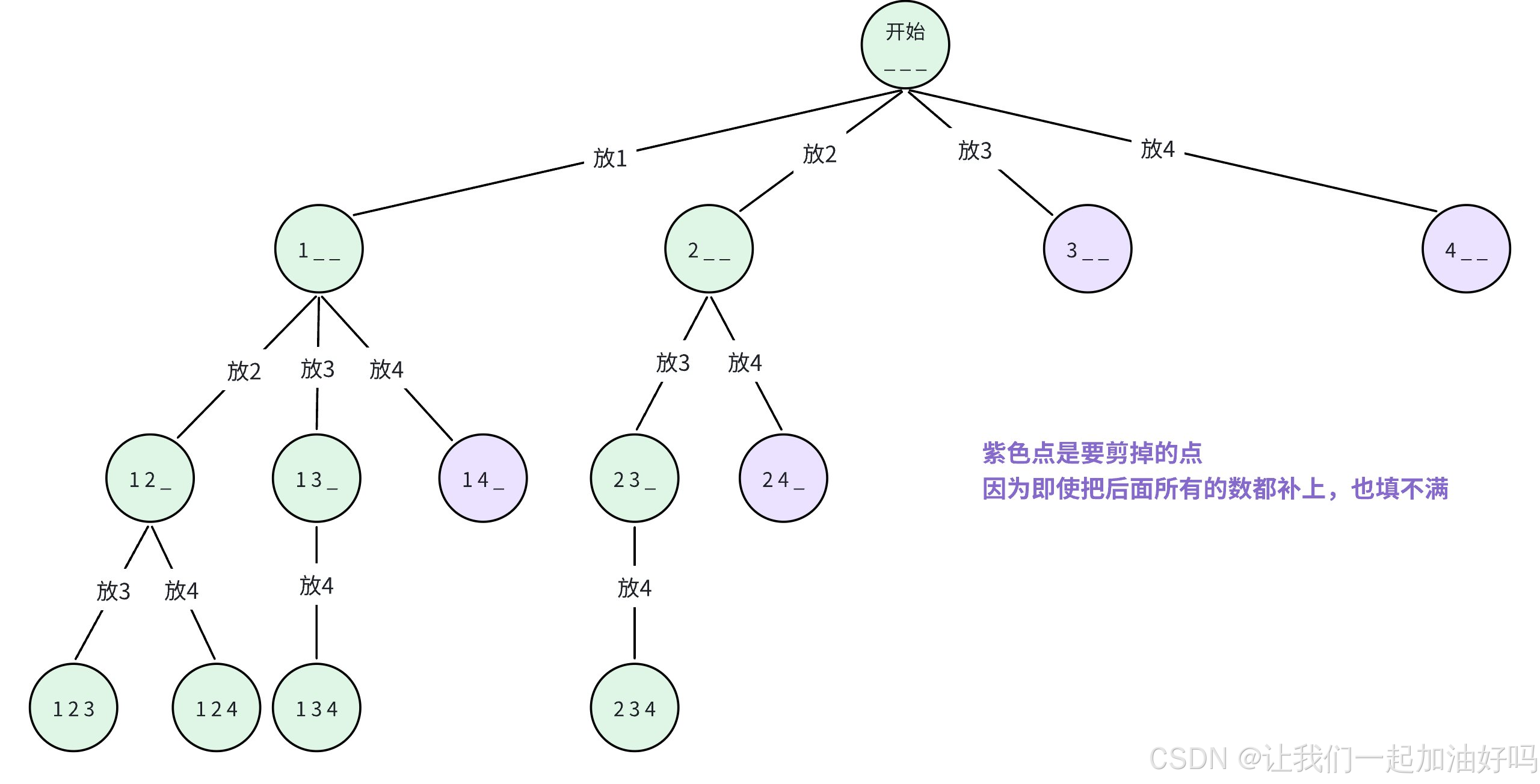
首先畫出決策樹：

解法同【枚舉排列】，唯一不同的是遞歸出口不同。

---

(2) 代碼實現

#include<iostream>
#include<vector>using namespace std;const int N = 10;int n;
vector<int> path;
bool vis[N];void dfs()
{if(path.size() == n){for(auto e : path) cout << "    " << e;cout << endl;return;}for(int i = 1; i <= n; i++){if(!vis[i])  // 如果當前數沒有被選擇{path.push_back(i);vis[i] = true;dfs();  // 遞歸到下一層path.pop_back();  // 恢復現場vis[i] = false;  // 恢復現場}}
}int main()
{cin >> n;dfs();return 0;
}