題目描述

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
輸入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
輸出：6
解釋：上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。

示例 2：
輸入：height = [4,2,0,3,2,5]
輸出：9

提示：
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

思考一（動態規劃）

可能一開始琢磨著怎么統計連續的接水區域面積，想不到把柱子形成的洼地分解成一個個柱子寬度大小的單位水桶進行計算，如下圖：

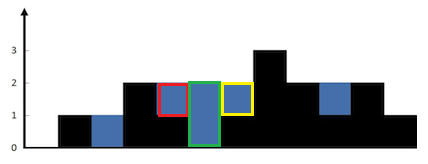
洼地分解成每個柱子寬度的水桶，只要確定這個水桶左右邊界（木板）的高度最小值就能計算這個柱子的接水量了。比如圖中的紅色區域柱子，它的左邊木板高度是 2，是左邊所有柱子高度的最大值，這個木板高度為什么取左邊最大值？顯然，左邊最高的木板能擋住更多的水，如果左邊最高的木板離當前柱子比較遠，那接水的面積可能更大。同理右邊木板最大高度是右邊所有柱子中高度最大的。現在確定了當前水桶（柱子）的左右木板高度，那么實際水桶的接水量就取決于兩個木板最短的那個減去當前柱子的高度，即 $water[i]=Min(leftSide,rightSide)?height[i]$。上圖中的紅色部分接水量 $w=Math.min(2,3)?1=1$。定義兩個數組 leftMax 和 rightMax 用于分別存儲每個柱子左右木板的最大值，初始化 leftMax = height[0], rightMax = height[height.length-1]，分別正序遍歷和倒序遍歷數組更新leftMax[i] 和 rightMax[i]，每次遍歷的高度與數組存儲的之前最大高度比較取最大值，這是動態規劃思想。最后遍歷高度數組 height，根據預處理的當前柱子左右木板高度和當前柱子高度很容易計算當前柱子的接水量，累加所有柱子接水量就是整個題目的答案。

算法過程

1. 初始化兩個數組 leftMax 和 rightMax，分別用于存儲每個位置左側和右側的最大高度
2. 正序遍歷高度數組，計算 leftMax[i]：每個位置左側的最大高度（包含當前位置）
3. 倒序遍歷高度數組，計算 rightMax[i]：每個位置右側的最大高度（包含當前位置）
4. 遍歷每個位置，計算該位置可接水量：Math.min(leftMax[i], rightMax[i]) - height[i]
5. 累加所有位置的接水量，得到總接水量并返回，時間復雜度$O(n)$，空間復雜度$O(n)$。

代碼

/*** @param {number[]} height* @return {number}*/
var trap = function(height) {const len = height.length;const leftMax = new Array(height