?演示基于PaddlePaddle自動求導技術實現梯度下降，簡化求解過程。

01、梯度下降法

梯度下降法是機器學習領域非常重要和具有代表性的算法，它通過迭代計算來逐步尋找目標函數極小值。既然是一種迭代計算方法，那么最重要的就是往哪個方向迭代，梯度下降法選擇從目標函數的梯度切入。首先需要明確一個數學概念，即函數的梯度方向是函數值變化最快的方向。梯度下降法就是基于此來進行迭代。

圖2.28對應一個雙自變量函數

。想要求得該函數極小值，只需要隨機選擇一個初始點，然后計算當前點對應的梯度，按照梯度反方向下降一定高度，然后重新計算當前位置對應的梯度，繼續按照梯度反方向下降。按照上述方式迭代，最終就可以用最快的速度到達極小值附近。

?

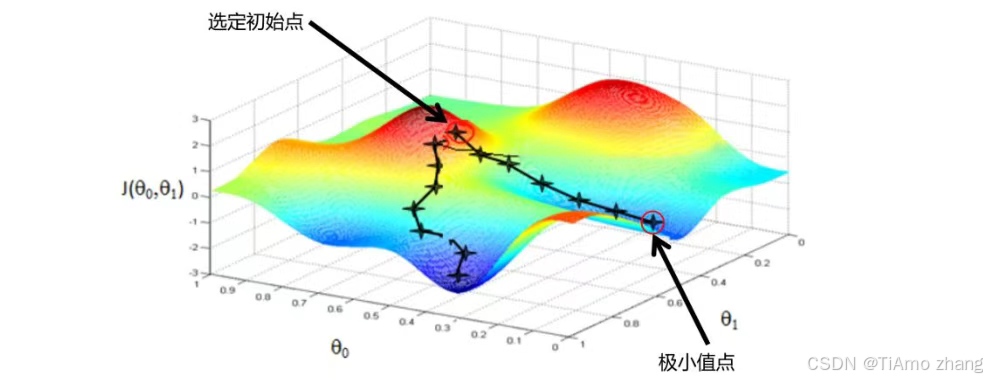
如果函數很復雜并有多個極小值點，那么選擇不同的初始值，按照梯度下降算法的計算方式很有可能會到達不同的極小值點，并且耗時也不一樣。因此，在工程實現上選擇一個好的初始值是非常重要的。

對于前面的直線擬合任務來說，其目標函數就是L，模型參數就是a和b。按照梯度下降算法的原理，對應實現步驟如下：

（1）初始化模型參數a和b；

（2）輸入每個樣本x，根據公式y=ax+b計算每個樣本數據的預測輸出值

；

（3）計算所有樣本的預測值

和真值y之間的平方差L；

（4）計算當前L對模型參數a和b的梯度值，即

；

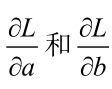
按照下式更新參數a和b：

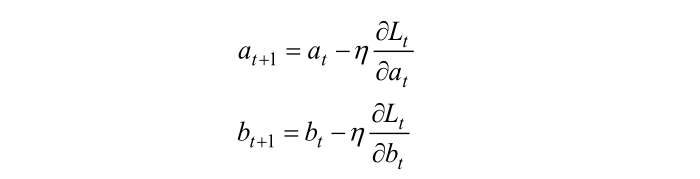
其中t表示當前迭代的輪次，

是一個提前設置好的參數，這個參數的作用是代表每一步迭代下降的跨度，專業術語也叫學習率；

（6）重復步驟（2）~（5），直至迭代次數超過某個預設值。

注意到，上述算法第（5）步中，需要計算目標函數L對a和b的偏導。盡管對于這個直線擬合任務來說其偏導求取非常簡單，但是依然需要手工進行求導。在2.3.3節中，介紹過可以通過PaddlePaddle來自動計算梯度，因此，可以使用PaddlePaddle來更便捷的實現這個梯度下降算法。

完整代碼如下（machine_learning/auto_diff.py）：

import matplotlib.pyplot as plt
import numpy as np
import paddle
# 輸入數據
x_train = np.array(    [3.3, 4.4, 5.5, 6.7, 6.9, 4.2, 9.8, 6.2, 7.6, 2.2, 7, 10.8, 5.3, 8, 3.1],    dtype=np.float32,)
y_train = np.array(    [17, 28, 21, 32, 17, 16, 34, 26, 25, 12, 28, 35, 17, 29, 13], dtype=np.float32)
# numpy轉tensor
x_train = paddle.to_tensor(x_train)
y_train = paddle.to_tensor(y_train)
# 隨機初始化模型參數
a = np.random.randn(1)
a = paddle.to_tensor(a, dtype="float32", stop_gradient=False)
b = np.random.randn(1)
b = paddle.to_tensor(b, dtype="float32", stop_gradient=False)
# 循環迭代
for t in range(10):# 計算平方差損失   y_ = a * x_train + b loss = paddle.sum((y_ - y_train) ** 2)# 自動計算梯度loss.backward()# 更新參數（梯度下降），學習率默認使用1e-3a = a.detach() - 1e-3 * float(a.grad)b = b.detach() - 1e-3 * float(b.grad)a.stop_gradient = Falseb.stop_gradient = False# 輸出當前輪的目標函數值Lprint("epoch: {}, loss: {}".format(t, (float(loss))))
# 訓練結束，終止a和b的梯度計算
a.stop_gradient = True
b.stop_gradient = True
# 可視化輸出
x_pred = paddle.arange(0, 15)
y_pred = a * x_pred + b
plt.plot(x_train.numpy(), y_train.numpy(), "go", label="Original Data")
plt.plot(x_pred.numpy(), y_pred.numpy(), "r-", label="Fitted Line")plt.xlabel("investment")
plt.ylabel("income")plt.legend()plt.savefig("result.png")
# 預測第16年的收益值
x = 12.5
y = a * x + b
print(y.numpy())

?上述代碼對每輪迭代的目標函數進行了輸出，同時預測了第16年的收益值，結果如下：

epoch: 0, loss: 9141.90625
epoch: 1, loss: 1103.665283203125
epoch: 2, loss: 397.5347900390625
epoch: 3, loss: 335.0281982421875
epoch: 4, loss: 329.02337646484375
epoch: 5, loss: 327.982421875
epoch: 6, loss: 327.381103515625
epoch: 7, loss: 326.8223571777344
epoch: 8, loss: 326.2711486816406
epoch: 9, loss: 325.72442626953125
[44.96492]

可以看到，隨著迭代的不斷進行，目標函數逐漸減少，說明模型的預測輸出越來越接近真值。最終訓練好的模型所預測的第16年的收益值與上一節使用導數法求解的標準解非常接近，驗證了梯度下降算法的有效性。

梯度下降法擬合結果如圖2.29所示。

?

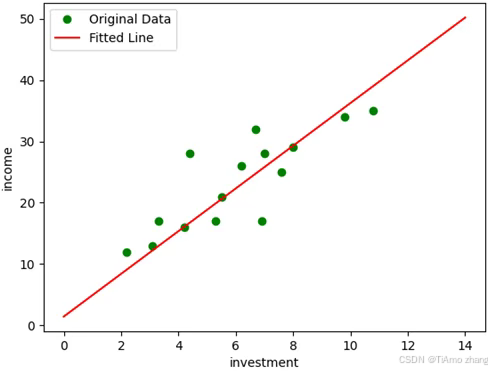
從擬合結果看到，利用PaddlePaddle自動幫助求導，通過梯度下降迭代更新模型參數，最后得到了令人滿意的結果，擬合出來的直線基本吻合數據的分布。整個過程不需要手工計算梯度，實現非常簡單。

注意，上述代碼使用了隨機值來初始化模型參數，因此每次運算的結果可能略有不同。另外，使用了固定的學習率1e-3，并得到了一個比較好的訓練結果。如果訓練過程中目標函數沒有逐步下降，那么就需要適當調整學習率重新訓練。

本節案例是一個非常簡單的使用PaddlePaddle進行機器學習的示例，旨在幫助讀者熟悉和鞏固PaddlePaddle的基本使用方法。雖然任務簡單，但是該示例“五臟俱全”，整個建模學習過程分為4個部分，如圖2.30所示。

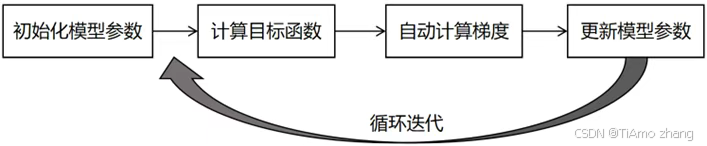
?對于后面的深度學習任務，也會按照上述方式進行模型訓練。下面正式開始介紹如何基于PaddlePaddle實現更復雜的深度學習圖像應用。