導讀：

在復雜網絡中，挖掘重要節點對精準推薦、交通管控、謠言控制和疾病遏制等應用至關重要。為此，本文提出一種局部信息驅動的節點重要性排序算法Leaky Noisy Integrate-and-Fire (LNIF)。該算法通過獲取節點的二階鄰居信息計算節點重要性，首先通過信息量衡量節點重要性，然后疊加符合條件的鄰居節點重要性，進一步區分節點重要程度，最終獲得節點排序。為驗證LNIF的有效性，在11個真實數據集和1個網絡模型上進行了實驗，采用平均度、網絡效率、最大連通子圖系數和SIR傳播模型四個指標進行對比分析。實驗結果表明，LNIF生成的節點序列在多個關鍵指標上表現顯著優于現有基準方法。LNIF計算出的節點序列使網絡平均度、網絡效率和最大連通子圖系數下降最快，表明其在優化網絡結構和識別關鍵節點方面效率更高；在SIR傳播模型中，LNIF的節點序列傳播能力也優于其他五種算法，進一步證明了其在遏制和引導信息傳播方面的潛力。

關注漢斯，獲取更多論文資訊，如您需要論文原文，歡迎私信獲取~

作者信息：

高 穎*,?董潔霜,?潘 杰,?周亦威,?朱美宣：上海理工大學管理學院，上海

正文

本文提出LNIF算法，結合二階鄰居信息和信息傳播因素，通過計算節點信息量并引入傳播閾值修正，提升準確性。在11個真實數據集和1個網絡模型上的實驗顯示，LNIF在平均度、網絡效率、最大連通子圖系數和SIR傳播模型中表現最優，能有效識別重要節點并產生最大影響力。

一. 材料和方法

算法描述：

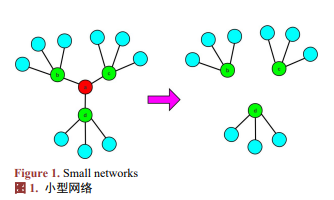
通常認為，網絡中度數最大的節點最重要，但實際上節點的重要性不僅取決于度數，還與鄰居節點的信息貢獻有關。若根據節點的度數來確定節點的重要性，則可能會忽略節點的信息，如圖1中的節點a。但是LNIF算法綜合考慮了節點的二階內鄰居信息以及信息傳播的因素來衡量節點的重要性值，若某節點的LNIF值越大，則說明該節點在網絡中越不能被替代，其重要性就越高，節點就越重要。

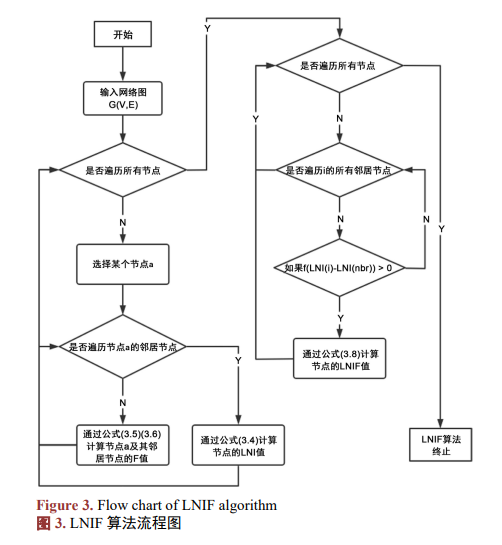
LNIF算法流程圖：

在本文中將采用網絡平均度、網絡效率、最大連通子圖系數和SIR傳播模型這4個指標來衡量LNIF算法的優越性。

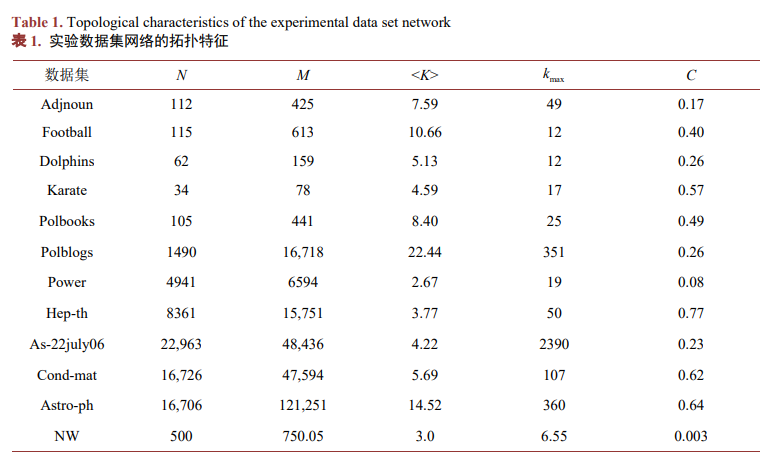
由于不同的網絡具有不一樣的結構與特征，為了驗證LNIF算法的有效性，本文共使用12個數據集，包括真實網絡數據集11個以及1個人工模擬網絡NW，數據集的拓撲統計特征如表1所示。其中N和M分別代表數據集網絡總節點數與總連邊數，?k??表示平均度數，Kmax?表示網絡中節點的最大度數，C表示網絡中的平均集聚系數。

二、結果

1. 平均度結果

本文所有實驗均采用Python 3.7。

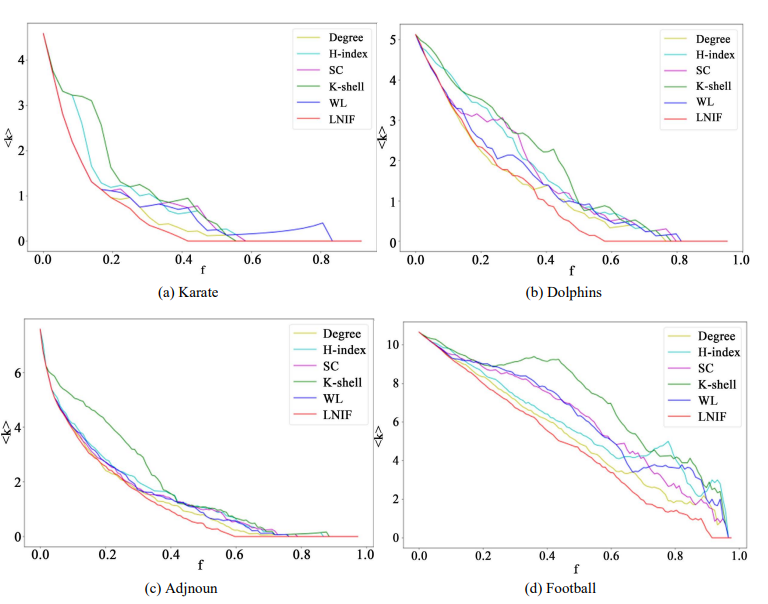
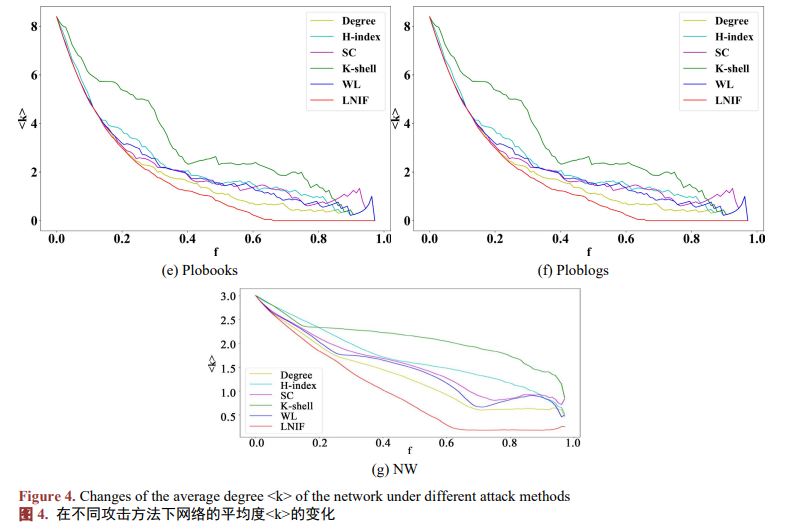
圖4展示了不同節點重要性算法下，移除節點后網絡平均度的變化，橫坐標f表示移除節點比例，縱坐標表示平均度變化。實驗結果如圖4(a)~(f)所示。在圖4(a)的karate網絡中，LNIF算法在移除相同比例節點時下降最快，前20%與WL、SC、Degree算法曲線重合，超過20%后LNIF曲線位于左下方，最先使?k??降至0。圖4(b)的Dolphins網絡中，前40%時LNIF與Degree算法曲線接近，超過40%后LNIF曲線下降最快，僅需移除約60%節點即可使?k??降至0，而其他算法需移除約80%。???????圖4(c)的Adjnoun網絡中，前30%時LNIF與Degree算法位于左下方，超過30%后LNIF曲線下降最快，最先使?k??降至0。圖4(d)的Football網絡中，前10%時除H-index和K-shell外，其余算法曲線接近，超過10%后LNIF曲線位于最下方。???????圖4(e)的Polbooks網絡中，LNIF曲線與圖4(a)類似，超過20%后表現最優。???????圖4(f)的Polblogs網絡中，除K-shell外，各算法曲線接近，但LNIF仍位于最下方。???????圖4(g)的NW網絡模型中，LNIF曲線下降幅度更大，更為陡峭。

后面的網絡效率結果、最大連通子圖系數結果、SIR實驗結果可點擊原文鏈接進行查看。

三、討論

結構上來說分為基于局部信息和基于全局信息來衡量節點的重要性。本文在此總結對比了幾種經典的節點重要性算法，詳見表2。

在上述實驗中，K-shell算法表現較差，主要原因是其將節點分層的結果是粗粒度的，無法區分同數值節點的重要性。H-index算法也存在類似問題，部分H-index值相同的節點在網絡中的重要性可能不同，導致結果不夠精確。相比之下，本文提出的LNIF算法表現優異，在幾乎所有數據集中均表現最佳。綜合平均度、網絡效率、最大連通子圖系數以及SIR實驗結果，LNIF算法在多數網絡中優于現有的Degree、H-index、WL、SC和K-shell算法。?

四、結論

在復雜網絡中，核心節點處于網絡中的優勢地位，挖掘核心節點具有重要的意義。為了挖掘網絡中的重要節點，本文提出一種考慮了節點的拓撲信息以及信息傳播的影響的LNIF算法，與基于全局信息的算法相比，該算法只需要計算節點的二階內鄰居信息即可計算節點的重要性值，對于挖掘、尋找大規模網絡中的關鍵節點具有現實意義。

原文鏈接：https://doi.org/10.12677/mos.2025.144301