0 序言

本文將深入探討決策樹算法，先回顧下前邊的知識，從其基本概念、構建過程講起，帶你理解信息熵、信息增益等核心要點。

接著在引入新知識點，介紹Scikit - learn 庫中決策樹的實現與應用，再通過一個具體項目的方式來幫助你掌握決策樹在分類和回歸任務中的使用，提升機器學習實踐能力。

【項目在下文第四節，原理已經搞懂了前3節可跳過！！！】

1 決策樹算法概述

1.1 決策樹的基本概念

決策樹是一種常見的機器學習算法，通過樹狀結構對數據進行分類或回歸，模仿人類決策過程，利用一系列判斷條件逐步劃分數據。

其主要組成元素包括：

• 根節點（Root Node）：包含完整數據集的起始節點，是決策樹的開端，所有數據最初都從這里開始進行劃分。

• 內部節點（Internal Node）：表示一個特征或屬性，用于對數據進行進一步的判斷和劃分。例如在預測水果類別時，內部節點可能是 “顏色” 這個特征。

• 分支（Branch）：表示決策規則，基于內部節點特征的不同取值而產生不同的分支。比如在顏色節點下，可能有紅色、綠色等分支。

• 葉節點（Leaf Node）：表示決策結果，當數據經過一系列內部節點的判斷和分支后，最終到達葉節點，得到相應的分類或回歸值。如經過多個特征判斷后，葉節點給出水果是蘋果的結論。

也可參照下圖作進一步理解。

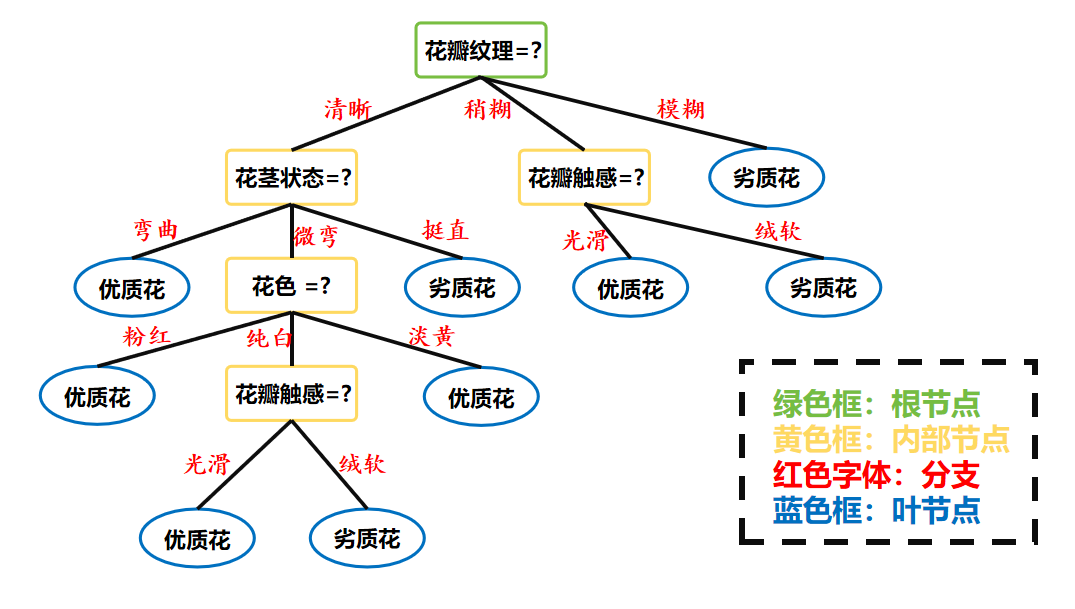
1.2 決策樹的優缺點

1.2.1 優點

• 易于理解和解釋：決策樹以直觀的樹狀結構呈現，其規則可清晰解讀，方便人們理解模型的決策邏輯。例如，通過觀察樹結構，能直接明白根據哪些特征如何做出最終決策。

• 較少的數據預處理需求：無需對數據進行復雜的歸一化或標準化處理，可直接處理數值型和類別型數據。像在處理客戶購買行為數據時，年齡（數值型）和性別（類別型）可同時作為特征輸入決策樹。

• 能處理多輸出問題：可同時對多個目標變量進行預測，適用于復雜的多任務場景。如在預測天氣狀況時，可同時預測溫度、濕度、天氣類型等多個指標。

1.2.2 缺點

• 容易過擬合：決策樹可能過度學習訓練數據中的細節和噪聲，導致對新數據的泛化能力差。例如，訓練數據中存在一些偶然因素，決策樹可能將其當作普遍規律學習，在預測新數據時出錯。

• 對數據中的噪聲敏感：數據中的噪聲可能誤導決策樹的構建，影響模型準確性。比如錯誤標注的數據可能導致決策樹生成不合理的分支。

• 可能偏向大量級別的屬性：在構建決策樹時，算法可能傾向于選擇取值較多的屬性進行劃分，而這些屬性不一定對分類或回歸最有價值。

2 決策樹的構建過程

2.1 特征選擇

特征選擇是決策樹構建的核心環節，目的是選擇最佳劃分特征，使劃分后的數據集純度更高。

常用的特征選擇標準如下：

• 信息增益（Information Gain）：基于信息熵的減少量來選擇特征。信息熵用于度量樣本集合的純度，信息熵越小，集合純度越高。ID3 算法采用信息增益。例如，對于一個包含是否購買商品標簽的數據集，計算年齡、性別等特征的信息增益，選擇信息增益最大的特征作為當前節點的劃分特征，這樣能最大程度降低數據集的不確定性。

• 信息增益比（Gain Ratio）：對信息增益進行改進，考慮了特征本身的熵。它能減少信息增益對取值數目較多屬性的偏好，C4.5算法使用信息增益比。例如，在某些數據集中，身份證號這種取值眾多的特征信息增益可能很大，但對分類并無實際意義，信息增益比可避免這種情況。

• 基尼指數（Gini Index）：衡量數據集的不純度，反映從數據集中隨機抽取兩個樣本，其類別標記不一致的概率。CART 算法使用基尼指數。基尼指數越小，數據集純度越高。

2.2 決策樹的生成

決策樹的生成是一個遞歸過程，主要步驟如下：

1. 從根節點開始：此時根節點包含全部數據集。例如，有一個預測動物類別的數據集，初始時所有數據都在根節點。

2. 計算所有可能的特征劃分：針對根節點的數據集，計算每個特征不同取值下的劃分情況。比如對于動物數據集，計算是否有翅膀、是否有毛發等特征不同取值時對數據集的劃分效果。

3. 選擇最佳劃分特征：根據信息增益、信息增益比或基尼指數等標準，選擇能使劃分后數據集純度最高的特征。假設通過計算信息增益，發現是否有毛發這個特征劃分后的數據集純度提升最大，則選擇它作為當前節點的劃分特征。

4. 根據該特征的取值創建子節點：根據所選特征的不同取值，將數據集劃分到不同的子節點。如 是否有毛發特征有是和否兩個取值，數據就被分到兩個子節點，每個子節點包含相應取值的數據子集。

5. 對每個子節點遞歸地重復上述過程：對每個子節點的數據子集，再次進行特征劃分、選擇最佳特征、創建新子節點等操作，直到滿足停止條件。停止條件通常包括節點中的樣本全部屬于同一類別、達到最大深度或節點中樣本數量過少等。例如，某個子節點的數據集中所有動物都屬于貓科動物類別，此時該子節點就成為葉節點，不再繼續劃分。

2.3 決策樹的剪枝

為防止決策樹過擬合，需要進行剪枝操作。剪枝分為預剪枝和后剪枝：

• 預剪枝（Pre - pruning）：在樹構建過程中提前停止。例如，在構建決策樹時，如果某個節點的劃分不能帶來決策樹泛化能力的提升（如通過驗證集評估），則停止劃分，將該節點標記為葉節點。還可以通過設置一些參數來實現預剪枝，如限制葉子節點的樣本個數，當樣本個數小于一定閾值時，不再繼續創建分支；或者設定信息熵減小的閾值，當信息熵減小量小于該閾值時，停止創建分支。

• 后剪枝（Post - pruning）：先構建完整樹，然后剪去不重要的分支。從已經構建好的完全決策樹的底層開始，對非葉節點進行考察，若將該節點對應的子樹替換成葉節點可以帶來決策樹泛化性能的提升（如在驗證集上錯誤率降低），則將該子樹替換為葉節點。例如，有一棵完整的決策樹，對某個非葉節點進行評估，發現將其下面的子樹替換為一個葉節點后，在驗證集上的準確率提高了，就進行此替換操作。

這里如果單獨看覺得比較抽象，可以看以下這個圖。

還是前面那張圖，假如為剪枝前的，

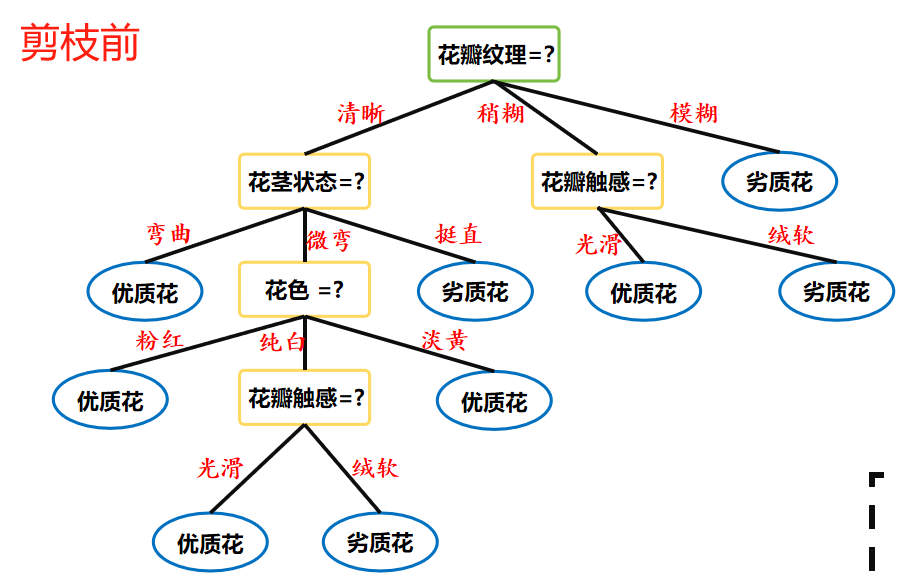
那么剪枝后就可能是這樣子。

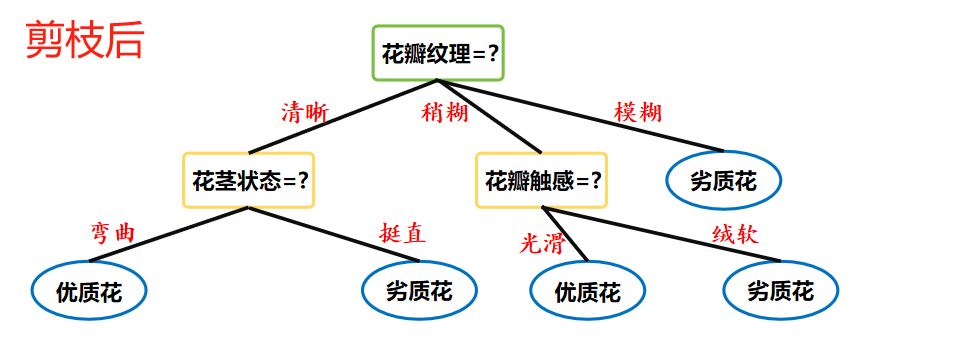
就相當于說，在不損失算法的性能的前提下，將比較復雜的決策樹，化簡為較為簡單的版本。

3 Scikit - learn中的決策樹 API

Scikit - learn提供了兩個主要的決策樹實現：

• DecisionTreeClassifier：用于分類問題，通過構建決策樹對數據進行分類預測。例如，預測客戶是否會購買某產品、郵件是否為垃圾郵件等。

• DecisionTreeRegressor：用于回歸問題，通過決策樹模型對連續型目標變量進行預測。比如預測房價、股票價格等。

3.1 DecisionTreeClassifier 參數詳解

class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0
)

• criterion：衡量分割質量的函數，可選值有：

• “gini”：基于基尼不純度，計算概率分布的基尼系數，反映數據集的不純度。

• “entropy”：基于信息增益，通過計算信息熵的減少量來衡量分割質量。

• “log_loss”：從 v1.3 版本開始新增，基于對數損失。默認值為gini。例如，如果數據集中類別分布較為均勻，使用entropy可能更合適，能更好地衡量信息增益。

• splitter：選擇每個節點分割的策略，可選值有：

• “best”：選擇最佳分割，通過計算所有可能的分割情況，找到使分割后數據集純度最高的方案。

• “random”：隨機選擇分割，這種方式可能更快，但結果不一定是最優的，可用于減少計算量或防止過擬合。默認值為best。

• max_depth：樹的最大深度，默認值為 None。當為 None 時，樹會一直擴展，直到所有葉子都是純的（即葉子節點中的樣本都屬于同一類別）或包含少于 min_samples_split 個樣本。如果設置為整數，如 5，則限制樹的最大深度為 5 層，可有效防止過擬合。

• min_samples_split：分割內部節點所需的最小樣本數，默認值為 2。可以是整數，表示絕對數量；也可以是浮點數，表示占總樣本的比例。例如，設置為 5，表示內部節點至少需要 5 個樣本才會進行分割；設置為 0.1，表示內部節點樣本數占總樣本數的比例至少為 10% 時才進行分割。

• min_samples_leaf：葉節點所需的最小樣本數，默認值為 1。同樣可以是整數或浮點數。例如，設置為 3，可防止創建樣本數過少的葉節點，避免模型過擬合。

• min_weight_fraction_leaf：葉節點所需的權重總和的最小加權分數，默認值為 0.0。當提供了 sample_weight（樣本權重）時使用，與 min_samples_leaf 二選一。例如，設置為 0.1，表示葉節點權重和必須大于等于總權重的 10%。

• max_features：尋找最佳分割時要考慮的特征數量，默認值為 None。可選值有：

• None / 不設置：考慮所有特征。

• “auto”/“sqrt”：表示考慮 <inline_LaTeX_Formula>\sqrt {n_features}<\inline_LaTeX_Formula > 個特征，其中 < inline_LaTeX_Formula>n_features<\inline_LaTeX_Formula > 是特征總數。

• “log2”：表示考慮 <inline_LaTeX_Formula>log2 (n_features)<\inline_LaTeX_Formula > 個特征。

• 整數：表示絕對數量的特征。

• 浮點數：表示占總特征的比例。該參數可影響訓練速度和模型隨機性，例如設置為 “sqrt”，可減少計算量，提高訓練速度。

• random_state：控制隨機性，默認值為 None。當為 None 時，使用隨機數生成器的默認狀態；當為整數時，作為隨機數生成器的種子，確保結果可重現。例如，設置 random_state = 42，多次運行代碼可得到相同的隨機結果，方便調試和對比實驗。

• max_leaf_nodes：最大葉節點數量，默認值為 None。當為 None 時，不限制葉節點數量；當為整數時，以最佳優先方式生長樹，可作為替代 max_depth 的剪枝方法。例如，設置為 10，可限制決策樹最多有 10 個葉節點，防止樹生長過大導致過擬合。

• min_impurity_decrease：分割節點需要的最小不純度減少量，默認值為 0.0。計算公式為 <inline_LaTeX_Formula>\frac {N_t}{N} \times (impurity - \frac {N_t_R}{N_t} \times right_impurity - \frac {N_t_L}{N_t} \times left_impurity)<\inline_LaTeX_Formula>，其中 < inline_LaTeX_Formula>N<\inline_LaTeX_Formula > 是總樣本數，<inline_LaTeX_Formula>N_t<\inline_LaTeX_Formula > 是當前節點樣本數。當某個節點的不純度減少量大于等于該值時，才會進行分割。

• class_weight：類別權重，默認值為 None。可選值有：

• None：所有類別權重為 1，即不考慮類別不平衡問題。

• “balanced”：自動計算權重，與類別頻率成反比，用于處理類別不平衡問題。例如，某個類別樣本數量很少，其權重會相應增大。

• 字典：手動指定 {class_label: weight}，可根據實際情況為每個類別設置權重。

• ccp_alpha：最小成本復雜度剪枝參數，默認值為 0.0。當為 0.0 時，默認不剪枝；當大于 0.0 時，較大的值會導致更多剪枝，可通過交叉驗證選擇最優值。例如，通過設置不同的 ccp_alpha 值，在驗證集上評估模型性能，選擇使模型泛化能力最佳的 ccp_alpha 值。

3.2 DecisionTreeRegressor 參數詳解

DecisionTreeRegressor與DecisionTreeClassifier的參數大部分相同，但criterion參數有所不同：

class sklearn.tree.DecisionTreeRegressor(criterion='squared_error', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, ccp_alpha=0.0
)

• criterion：衡量分割質量的標準，默認值為squared_error（均方誤差），可選值還有：

• “absolute_error”：平均絕對誤差。

• “friedman_mse”：弗里德曼均方誤差，考慮了數據集的特征數量和樣本數量對誤差的影響。

• “poisson”：泊松偏差，適用于目標變量服從泊松分布的數據。不同的 criterion 適用于不同的數據分布和問題場景，例如，當數據中存在較多異常值時，absolute_error可能比squared_error更穩健。

4 決策樹實戰示例

4.1 前期準備

導入需要的4個庫。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import classification_report, accuracy_score

pandas庫主要用于數據的結構化處理，比如數據清洗就要用到它；

numpy庫則是用于數值計算和數組操作。

matplotlib的pyplot模塊是用于繪制基礎圖表；

seaborn庫是為了繪制更美觀的統計圖表。

下面這四條程序與機器學習有關。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import classification_report, accuracy_score

• from sklearn.datasets import load_iris：從scikit-learn庫導入鳶尾花數據集

• from sklearn.model_selection import train_test_split：用于將數據集分割為用于模型訓練的訓練集和用于模型評估的測試集

• from sklearn.tree import DecisionTreeClassifier, plot_tree：

  • DecisionTreeClassifier：決策樹分類器類，用于構建決策樹模型
  • plot_tree：可視化決策樹結構的函數

• from sklearn.metrics import classification_report, accuracy_score：

  • accuracy_score：計算模型預測的準確率
  • classification_report：生成詳細的分類評估報告，包含精確率、召回率、F1分數等指標

這些庫組合起來，就是前期需要完成的準備工作。

4.2 加載并探索數據集

我們在拿到一個全新的數據集之前，由于一開始對數據集并不熟悉，

它到底有多少標簽，如何劃分，數據結構如何，

這些都是未知的，因此本小節的內容就很重要，

因為它是讓我們熟悉數據集，

只有充分熟悉數據集，你才能更好地去使用它作為數據支撐去訓練你的模型。

# Load iris dataset
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['species'] = iris.target# Map numeric targets to class labels
df['species'] = df['species'].map({i: name for i, name in enumerate(iris.target_names)})# Show dataset info
print("Dataset shape:", df.shape)
df.head()

下面針對以上程序進一步分析講解。

1. 加載鳶尾花數據集

iris = load_iris()

• load_iris() 是 sklearn 提供的加載鳶尾花數據集的函數
• 返回的 iris 是一個類似字典的對象，包含數據集的各種信息（特征數據、標簽、特征名稱等）

2. 構建DataFrame

df = pd.DataFrame(iris.data, columns=iris.feature_names)

• 將鳶尾花的特征數據（iris.data）轉換為 pandas 的 DataFrame 格式，方便后續處理
• columns=iris.feature_names 為 DataFrame 設置列名，這些列名是鳶尾花的4個特征名稱：
  • sepal length (cm)（花萼長度）
  • sepal width (cm)（花萼寬度）
  • petal length (cm)（花瓣長度）
  • petal width (cm)（花瓣寬度）

我在網上找了一張圖，可以參考這張圖標的參數具體在現實中花朵屬于哪個部位。

另外，

這里轉成DataFrame格式是為了給每列數據都加上具體的標簽，以便于后續數據處理，

原先數據集是個二維數組，只有純數字并沒有標簽。

3. 添加標簽列并映射為類別名稱

df['species'] = iris.target
df['species'] = df['species'].map({i: name for i, name in enumerate(iris.target_names)})

• 第一行：添加標簽列 species，iris.target 是原始的數值標簽（0、1、2）
• 第二行：將數值標簽映射為實際的鳶尾花品種名稱：
  • 0 → setosa（山鳶尾）
  • 1 → versicolor（變色鳶尾）
  • 2 → virginica（維吉尼亞鳶尾）
• 映射使用字典推導式，將 iris.target_names 中的品種名稱與索引對應起來。

4. 展示數據集信息

print("Dataset shape:", df.shape)
df.head()

• print("Dataset shape:", df.shape) 輸出數據集的形狀（樣本數×特征數）
• df.head() 顯示數據集的前5行數據。

一般的圖表，第一行基本都會寫上標簽，

我們快速了解表的結構和內容一般看頭五行基本就大概了解了，

我這里使用的數據集，鳶尾花數據集固定為 (150, 5)（150個樣本，4個特征+1個標簽）

運行以上程序，初步認識下數據集。

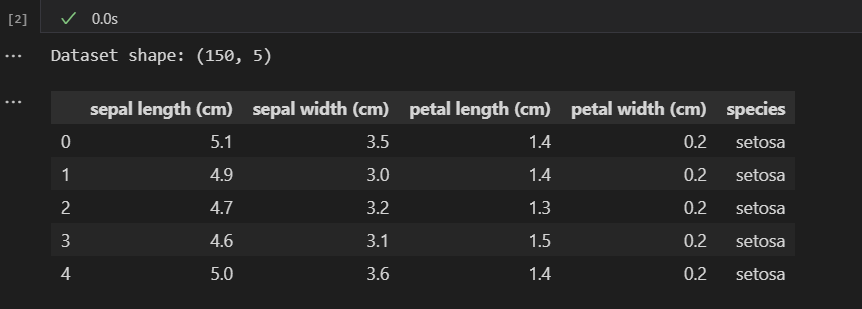
這里就清楚了，

通過這個結構化的鳶尾花數據集表格，

就清楚它包含4個特征列和1個品種標簽列，

那我們后續的數據分析和模型訓練就需要以它為標準。

4.3 可視化鳶尾花數據集特征分布

接著我們用圖表的形式來具體看看該數據集的特征分布，

同理，本小節的方法你用在其他數據集上也是同樣的道理，

可以說是必不可少的一步。

sns.pairplot(df, hue='species')
plt.suptitle("Feature Distribution by Species", y=1.02)
plt.show()

先對以上程序進行簡單的分析：

這里主要是借助 seaborn 的 pairplot 函數，從多個維度展示特征間關系與分布規律：

---

1. 核心：sns.pairplot(df, hue='species')

• sns.pairplot：
  是 seaborn 庫的配對圖函數，自動遍歷數據集所有數值特征，繪制兩兩特征的關系圖（含散點圖、直方圖），你可以借助這些圖來快速探索特征間相關性、分布規律。
• df：
  傳入預處理好的 DataFrame（含鳶尾花特征+標簽），pairplot 會自動解析其列數據。
• hue='species'：
  按 species 列（鳶尾花品種：setosa、versicolor、virginica）對數據上色區分，讓不同品種在圖中呈現不同顏色，可以更加直觀地對比分布差異。

2. 次要優化：plt.suptitle("Feature Distribution by Species", y=1.02)

• plt.suptitle：
  給整個圖像添加標題。
• y=1.02：
  調整標題位置。

3. 渲染輸出：plt.show()

• 觸發 matplotlib 渲染，將 pairplot 生成的所有子圖展示在窗口/Notebook 中。

看看運行的結果：

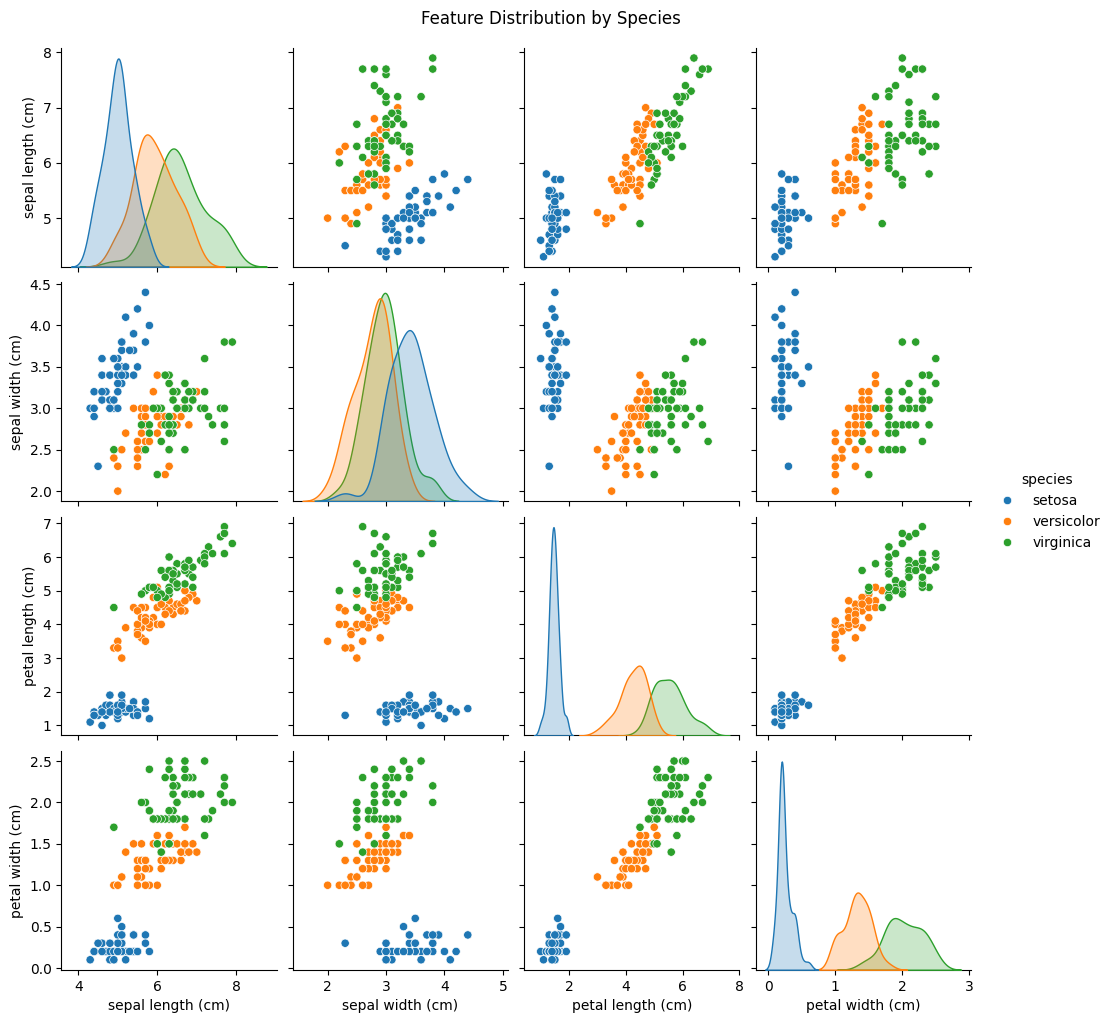
得到圖片后，我們要對圖片進行分析，

這里很重要，因為圖片分析好壞決定我們后續使用哪類特征去進行節點分類！！！

---

下面先對圖中畫紅框的圖片進行分析，

也就是對角線的那四個圖表，

準確來說，它應該是直方圖。

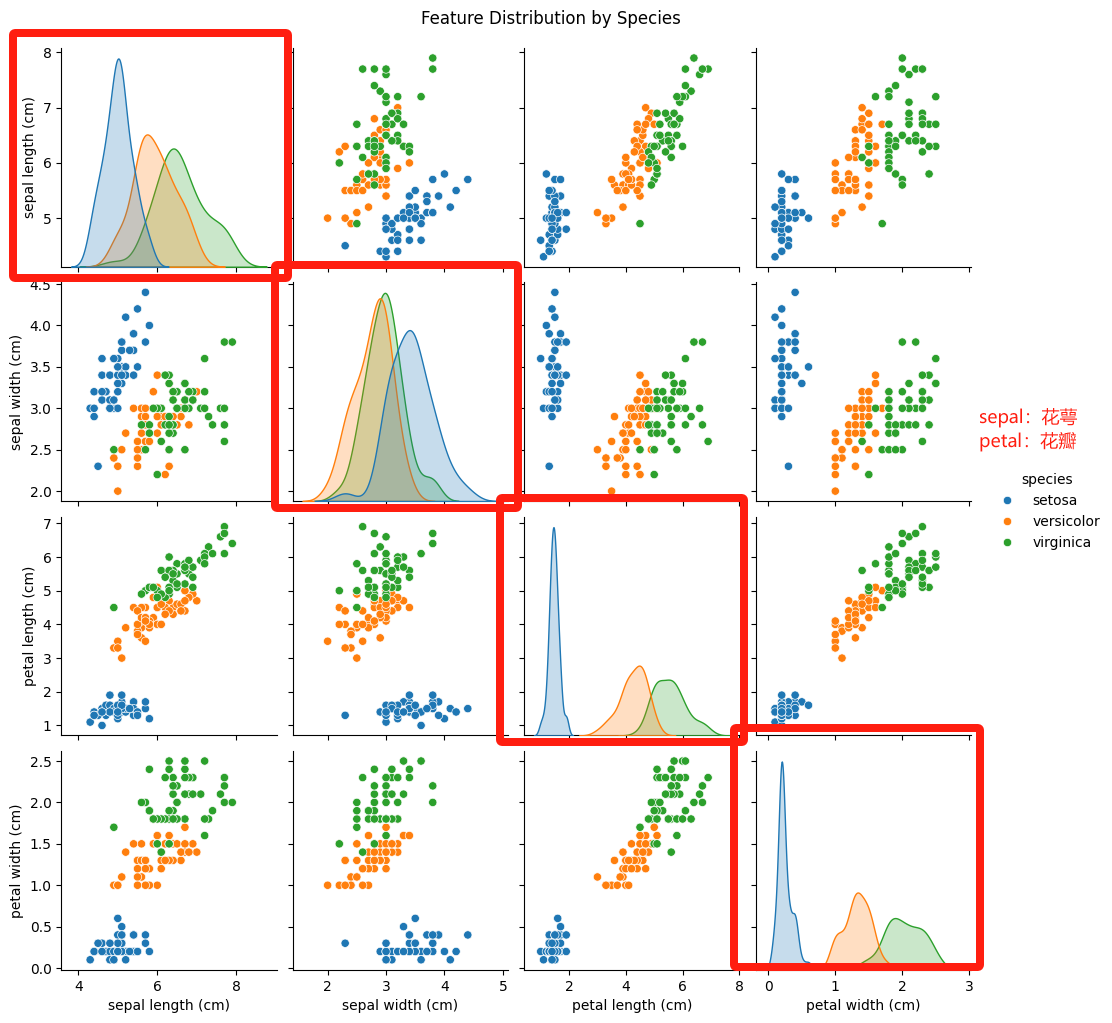
我們通過以下表格來認識區分它。

這里算是單特征分布的示意圖，展示單個特征在不同品種中的數值分布。

特征子圖	分布規律 & 品種差異
sepal length	setosa花萼長度明顯更小，集中在4.5-5.5cm；versicolor和 virginica重疊較多，范圍5-7cm
sepal width	setosa花萼寬度更大（3-4.5cm），另外兩個品種集中在2.5-3.5cm，重疊嚴重
petal length	setosa花瓣長度極小，versicolor集中在3-5cm，virginica集中在4.5-7cm，區分度極高
petal width	setosa花瓣寬度極小，versicolor集中在1-1.8cm，virginica集中在1.8-2.5cm，區分度很高

這四個圖分析完后，

還剩下12個圖，剩下的圖就是雙特征關聯的散點圖。

這些圖主要是展示特征間的關聯關系，以及不同品種的聚類規律。

這里我們從中挑選2張圖進行分析就好。

入下圖中用紅框標出來的圖，

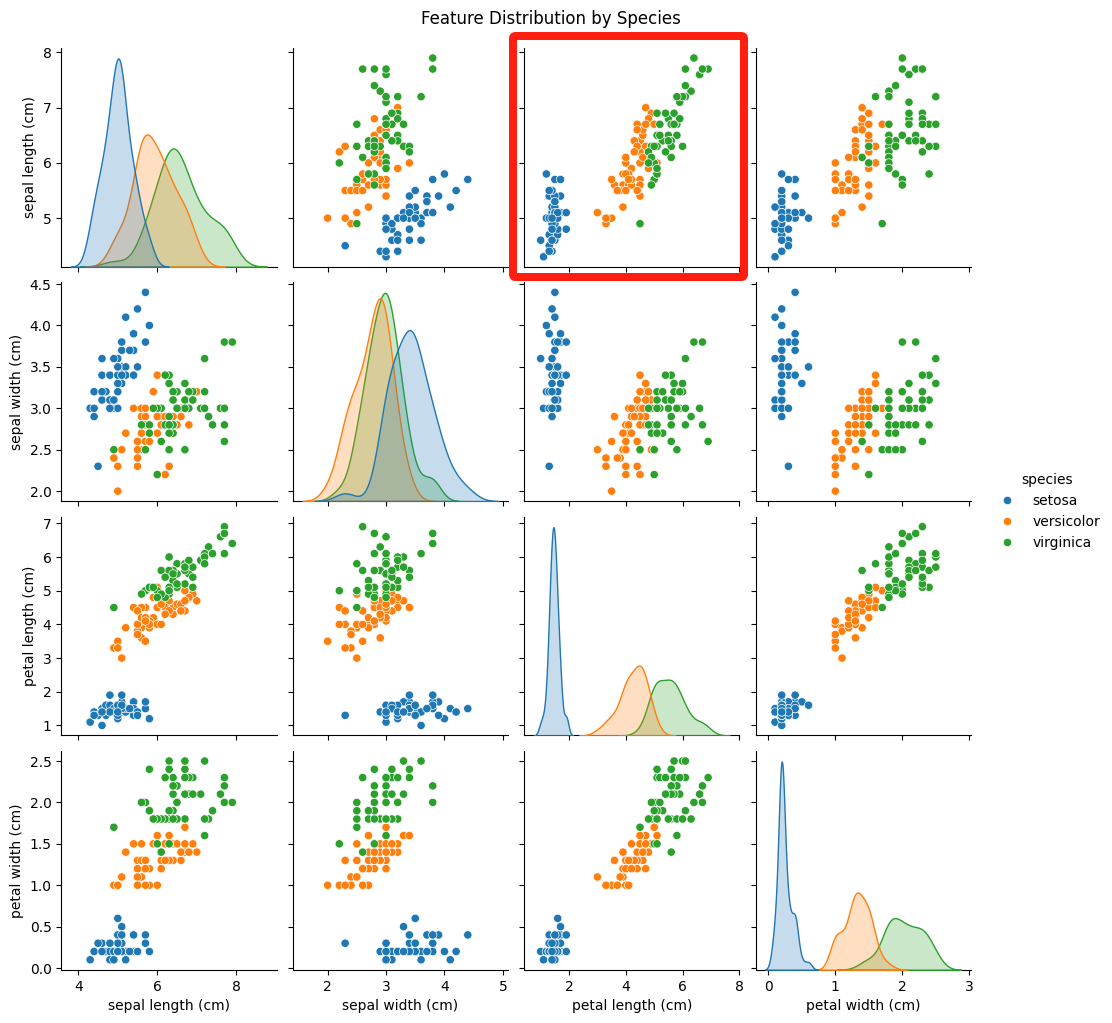
從這張圖中，我們可以注意到：

• setosa花瓣短、花萼也短，形成左下角的密集點；
• versicolor花瓣長度中等，花萼長度中等；
• virginica花瓣長、花萼也長，分布在右上角。

這里初步得出：花萼長度和花瓣長度正相關，且不同品種沿對角線分布，有一定區分度。

再來，我們再看下面這張圖：

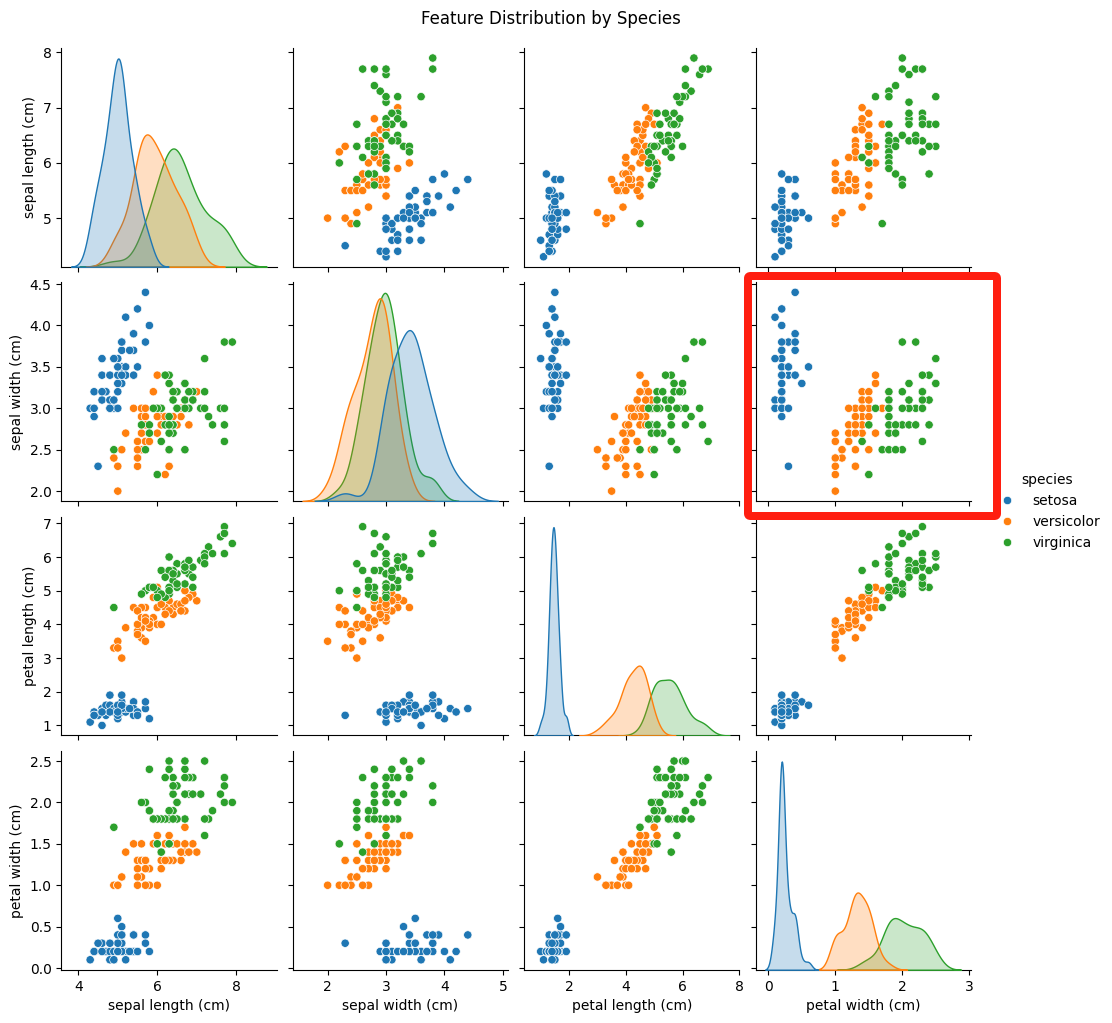
同理，可以觀察到：

• setosa花瓣寬度窄、花萼寬度寬，形成左上角的點；
• versicolor和 virginica花瓣寬度越大，花萼寬度也越大，但兩者重疊較多。

得出初步結論，發現花萼寬度和花瓣寬度弱正相關，setosa 與其他品種區分明顯，但versicolor和 virginica 難通過這對特征區分。

接著再通過比對右下角兩個圖以及左側三個正相關的圖，

最終得出如下總結：

1. 最具區分度的特征：petal length 和 petal width
2. 次優特征：sepal length（能輔助區分 versicolor 和 virginica）。
3. 最無效特征：sepal width（因為versicolor 和 virginica 重疊嚴重，難以單獨區分）。

這里尤其是 setosa 與其他品種的邊界非常清晰，

所以后續用決策樹/分類模型時，petal length 和 petal width 會優先成為分裂節點！！！

因為它們能最大程度降低分類不確定性；

而 sepal width 可能在深層節點才被使用，或對模型貢獻較小。

本小節雖然程序不多，理解難度也比較低，

但是核心難點在于我們如何通過得到的圖片進行判斷，

通過觀察分布和聚類規律，預判哪些特征對分類最有效，避免盲目建模，讓后續模型訓練更高效！

4.4 準備用于模型的數據

X = df.drop('species', axis=1)
y = df['species']# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)print("Training samples:", X_train.shape[0])
print("Testing samples:", X_test.shape[0])

老樣子，先對程序進行分析。

核心在于做數據準備，分為分離特征與標簽、劃分訓練集和測試集兩個關鍵步驟

1.分離特征（X）和標簽（y）

# Features and labels
X = df.drop('species', axis=1)
y = df['species']

• X = df.drop('species', axis=1)：

  • df 是包含鳶尾花數據的 DataFrame（有4個特征列 + 1個 species 標簽列）。
  • drop('species', axis=1) 表示刪除 species 這一列（axis=1 代表操作列），剩下的列作為特征數據（X），用于訓練模型輸入
  • 最終 X 包含4列：sepal length、sepal width、petal length、petal width。

• y = df['species']：

  • 提取 species 這一列作為標簽（y），作為模型需要預測的輸出

2.劃分訓練集和測試集

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

• train_test_split：
  這是 sklearn 提供的數據集拆分工具，作用是把特征（X）和標簽（y）隨機拆成兩部分：

  • 訓練集（X_train, y_train）：喂給模型學習規律;

  • 測試集（X_test, y_test）：驗證模型學得好不好;

  • test_size=0.3：選擇常見的37開，測試集占總數據的 30%，訓練集則占 70%；

  • random_state=42：固定隨機種子，讓每次拆分結果完全一致。

3.輸出數據集大小

print("Training samples:", X_train.shape[0])
print("Testing samples:", X_test.shape[0])

• X_train.shape[0] 取訓練集的樣本數量；
• X_test.shape[0] 取測試集的樣本數量；

驗證拆分比例是否正確，確保數據準備無誤。

本小節的內容也是比較重要的，

算得上是必經步驟，

后續再為模型準備數據的時候牢記三步走：

1. 分離特征X和標簽y，讓模型明確輸入和輸出；
2. 拆分訓練集/測試集，用訓練集學規律、測試集驗效果的方式，避免模型過擬合；
3. 固定 random_state 讓實驗可復現，方便調試和對比不同模型的效果。

這一步驟做好后，后續建模就可以直接用 X_train, y_train 訓練模型，再用 X_test, y_test 評估效果，整個流程就打通啦。

$$\begin{gathered} 150\times 30\%=45\text{（測試集樣本數）} \\ 150\times 70\%=105\text{（訓練集樣本數）} \end{gathered}$$

輸出的結果跟預期計算的結果是一致的，

這個流程就順利完成了。

4.5 訓練決策樹模型

clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)
clf.fit(X_train, y_train)

對程序進行分析，

clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)

• DecisionTreeClassifier：
  是 sklearn 決策樹分類器的類，初始化時通過參數配置模型的結構和訓練規則。

• 參數解釋見下表：

  參數名	作用	你的配置值
  criterion	決策樹分裂依據，可選 gini（默認）或 entropy（信息熵）	entropy
  max_depth	限制樹的最大深度，避免過擬合（值越小模型越簡單）	3
  random_state	固定隨機種子，讓每次訓練結果一致（可復現）	42

clf.fit(X_train, y_train)

• fit 是模型的訓練方法，傳入訓練集特征（X_train）和訓練集標簽（y_train），讓決策樹學習特征→標簽的映射規律。
• 訓練過程：決策樹根據 criterion='entropy' 計算信息熵，不斷分裂節點，直到樹深達到 max_depth=3，最終形成一棵有決策邏輯的樹。

這里對函數內部參數選擇的具體數值進行解析：

• criterion='entropy'：讓決策樹優先選擇信息增益大的特征分裂；
• max_depth=3：避免樹過深，讓模型更通用；
• random_state=42：能得到完全一樣的決策樹，否則每次訓練結果不同。

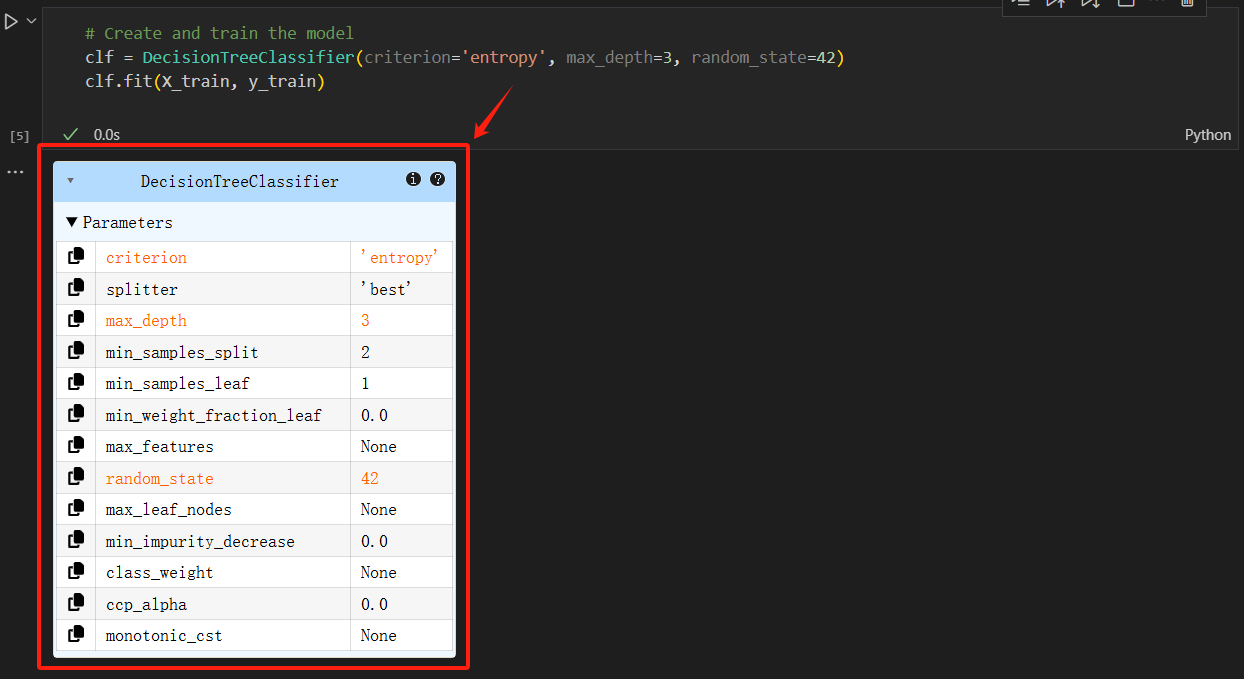
運行后這里就會顯示你設置的各類參數。

4.6 可視化決策樹

plt.figure(figsize=(15,10))
plot_tree(clf, filled=True, feature_names=X.columns, class_names=clf.classes_)
plt.title("🌳 Decision Tree Visualization", fontsize=16)
plt.show()

這段代碼將抽象的決策樹規則轉化為直觀的圖形，方便理解模型的分類邏輯。

1. plt.figure(figsize=(15,10))
創建一個繪圖窗口（畫布），指定畫布寬度為15英寸，高度為10英寸

這里根據具體要求來，數值越大，圖越清晰，如果要展示復雜的決策樹，可以在這個基礎上加點。

2. plot_tree(...)（核心可視化函數）

plot_tree(clf, filled=True, feature_names=X.columns, class_names=clf.classes_)

• plot_tree 直接將訓練好的決策樹（clf）轉化為圖形。
• 關鍵參數解析：
  • clf：傳入已訓練好的決策樹模型；
  • filled=True：為樹的節點填充顏色，顏色深淺表示節點的純度(純度越高，顏色越深，直觀區分不同類別占比)。
  • feature_names=X.columns：指定特征名稱，替代默認的 X[0]、X[1] 等抽象編號，讓節點的判斷條件更易讀。
  • class_names=clf.classes_：指定類別名稱（如 setosa、versicolor、virginica），替代默認的數字標簽，讓葉節點的分類結果更直觀。

3. plt.title("🌳 Decision Tree Visualization", fontsize=16)
為整個決策樹圖添加標題并設置標題字體大小為16。

4. plt.show()
用matplotlib渲染并顯示圖像，將繪制好的決策樹展示在屏幕上。

運行程序看看具體效果：

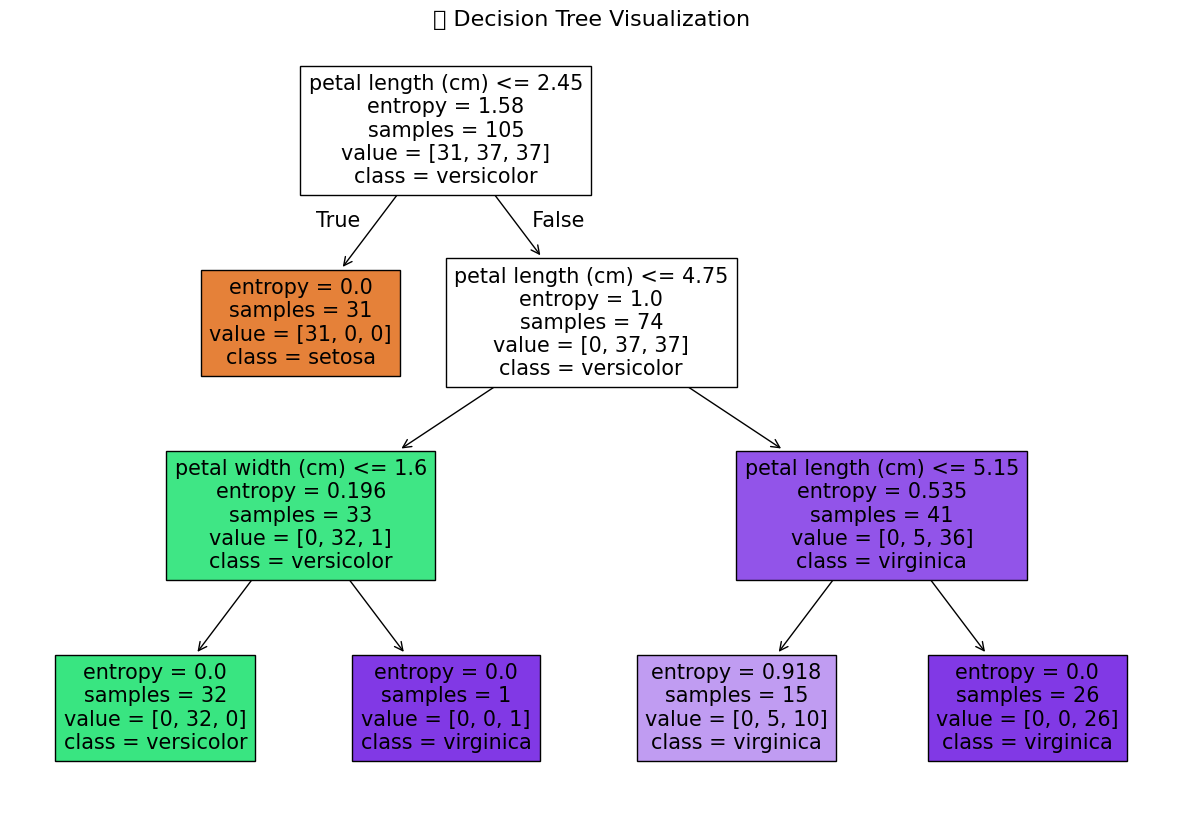
我們來對這張圖片進行分析：

首先來分析根節點，見下圖：

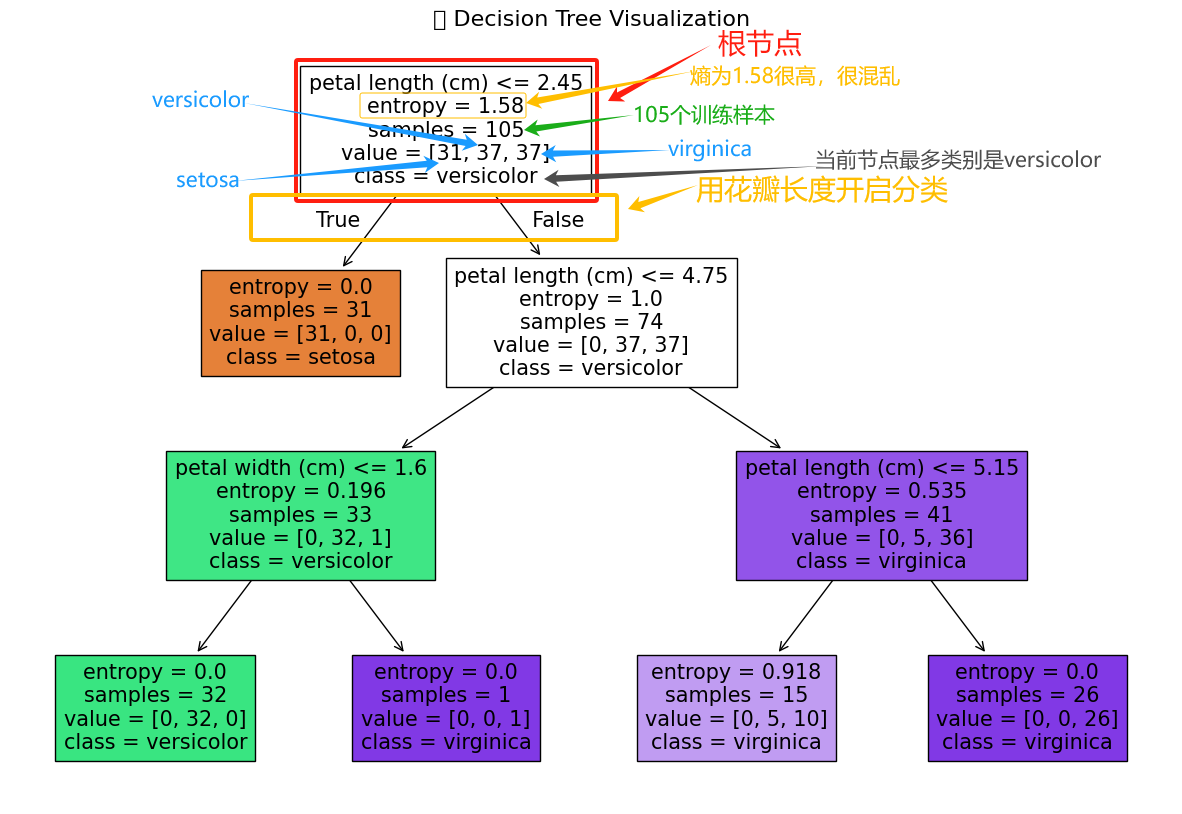
接下來看一下根節點的分支。

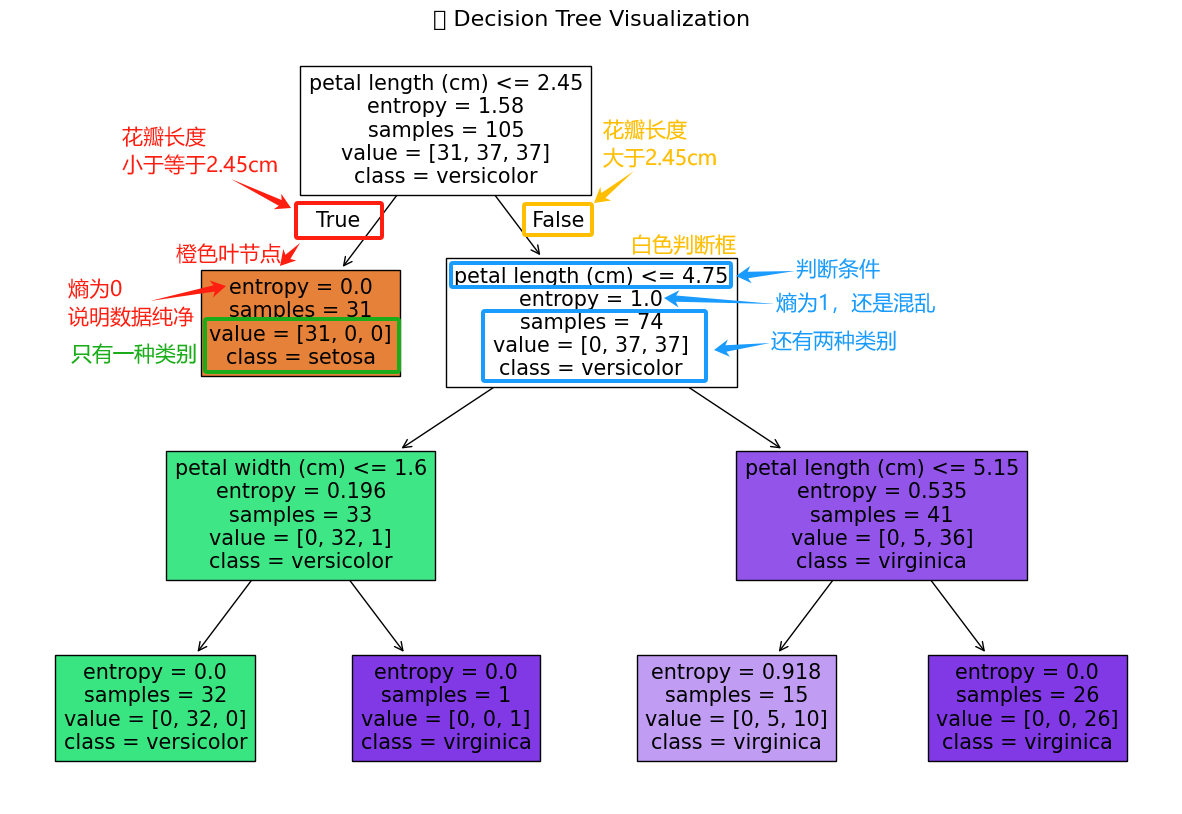
然后看一下第二層的分支。

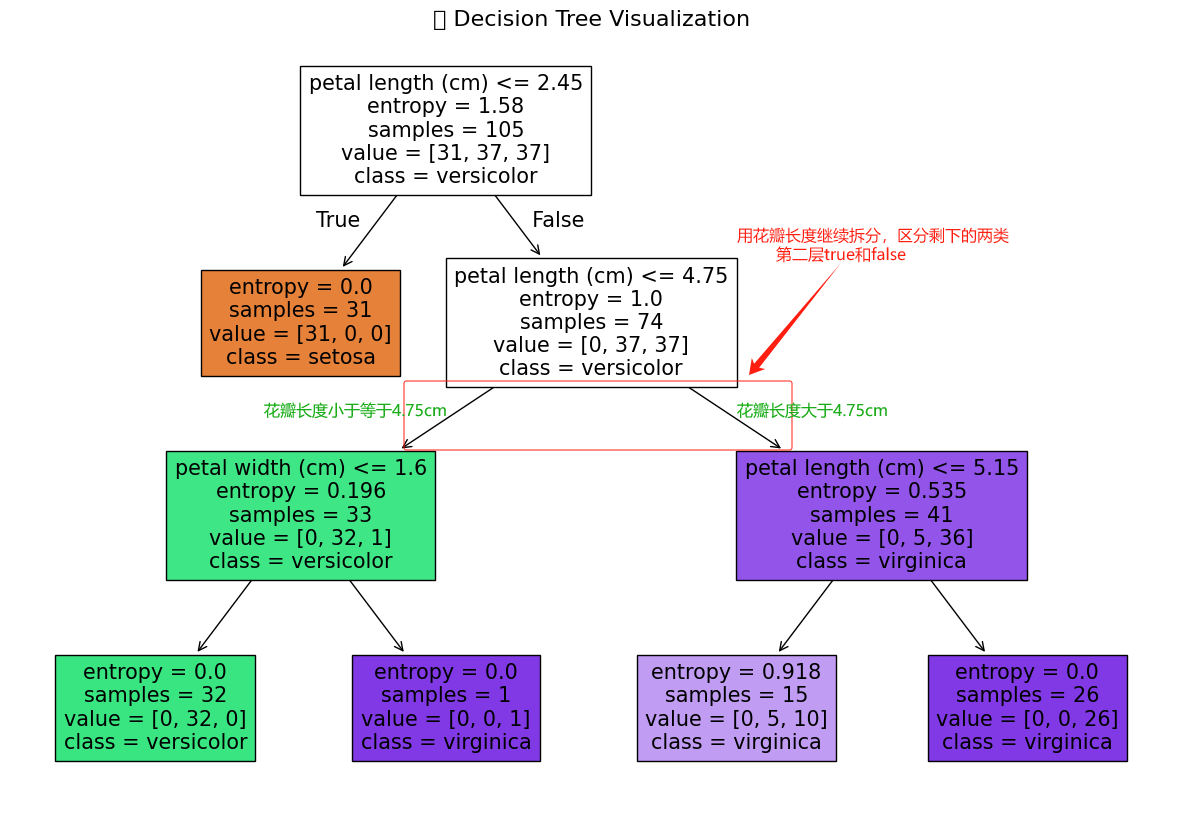
接著看一下第三層節點。

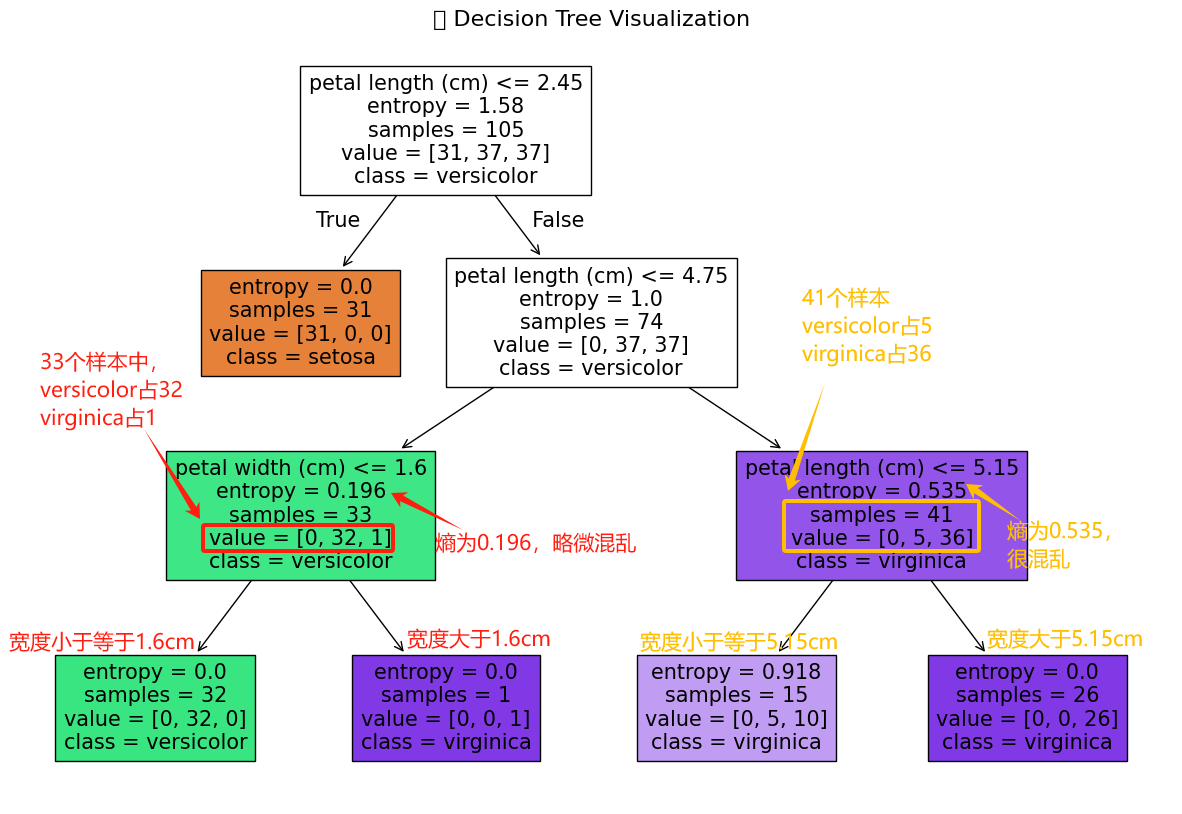
最后看一下葉節點

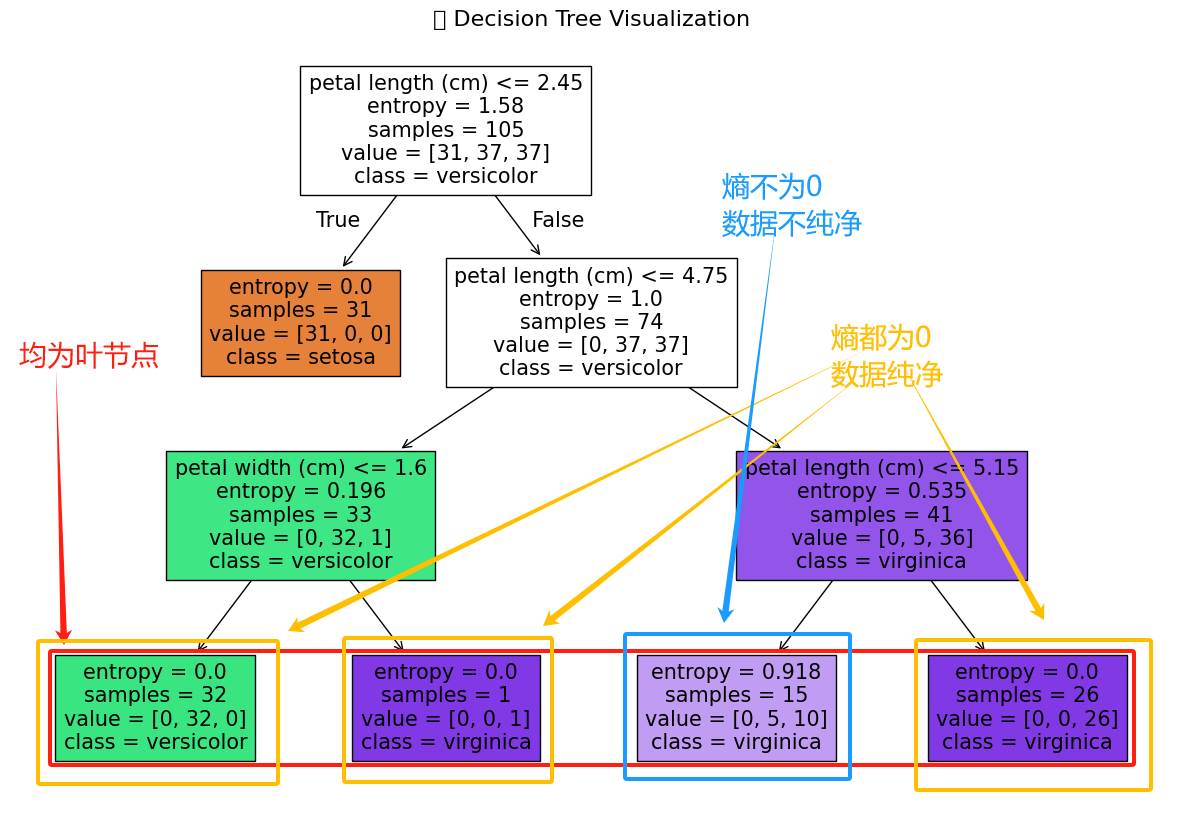
好啦，到這里圖片就都分析完了，

我們可以從中獲取到一些規律并進行總結。

分為3點來闡述：

1. 最關鍵的特征： petal length（花瓣長度）

根節點直接用它拆分，把 setosa 一鍵篩出；

第二層繼續用它拆分 versicolor 和 virginica。

2. 最明顯的邊界 → setosa 的花瓣長度

setosa 幾乎全部分布在花瓣長度 ≤2.45cm，和另外兩類完全分開。

3. 最易混淆的類別 → versicolor 和 virginica

前兩層篩不掉，需要靠 花瓣寬度（versicolor 窄）和 更長的花瓣長度（virginica 長）進一步區分。

總結：
在特征選擇方面，模型自動選 petal length 作為根節點，說明花瓣長度是區分鳶尾花最核心的特征，和我們之前可視化 pairplot 的結論一致！

但與此同時，還是發現過擬合風險，比如葉節點里，淺紫色節點熵 = 0.918，還有 5 個 versicolor 沒分干凈，這說明當樹深 = 3 時，仍有少量混雜，但整體不影響大分類。如果繼續加深樹（如 max_depth=4），可能會導致過擬合！

本小節用了大量篇幅來進行講解，就是為了說明一點，那就是通過可視化，我們能直觀看懂模型的決策邏輯，比如模型優先用哪個特征劃分數據，不同特征的判斷閾值是多少，最終如何得出分類結果。這對于理解模型、解釋預測結果，如“為什么這個樣本被分為 virginica”以及調參優化，如判斷樹深是否合適都非常重要！！！

4.7 評估模型

y_pred = clf.predict(X_test)print("🔍 Classification Report:\n")
print(classification_report(y_test, y_pred))print("? Accuracy Score:", accuracy_score(y_test, y_pred))

可以使用以上程序去評估一下這個模型，

通過預測結果與真實標簽的對比，從而量化模型的分類效果。

下面先分析下這段程序：

1. y_pred = clf.predict(X_test)

用訓練好的決策樹模型（clf）對測試集特征（X_test）進行預測，得到模型的預測標（y_pred）

在這個過程中，模型會根據之前學到的決策規則，對測試集中的45個樣本逐一判斷，輸出每個樣本的預測品種。

2. 輸出分類報告：classification_report(y_test, y_pred)

print("🔍 Classification Report:\n")
print(classification_report(y_test, y_pred))

classification_report 是 sklearn 提供的綜合評估工具，對比真實標簽（y_test）和預測標簽（y_pred），輸出每個類別的詳細指標，具體可以見下表：

指標	含義
precision	精確率：預測為某品種的樣本中，真正屬于該品種的比例
recall	召回率：該品種的真實樣本中，被模型正確預測出來的比例
f1-score	精確率和召回率的調和平均（綜合兩者，值越接近1越好）
support	該品種在測試集中的真實樣本數量（如測試集中有14個setosa）

最后， macro avg為宏平均，所有類別平等加權；

weighted avg為加權平均，按樣本數加權，評估模型整體表現。

3. 輸出準確率：accuracy_score(y_test, y_pred)

print("? Accuracy Score:", accuracy_score(y_test, y_pred))

準確率（Accuracy）：所有測試樣本中，預測正確的比例（正確預測數 / 總樣本數）。

我們運行一下程序，看看結果：

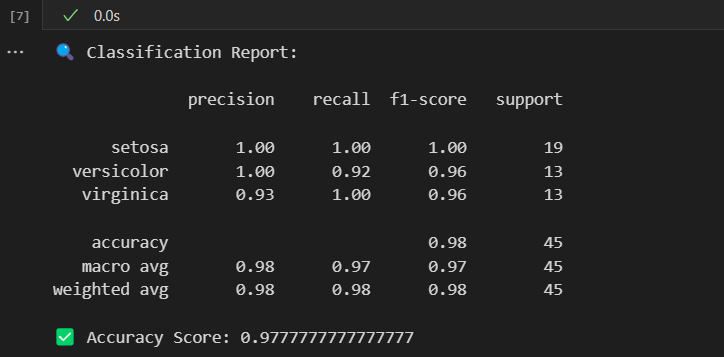
對圖片進行分析，

這里可以用一張表來概括說明更好。

1.逐類別分析（setosa、versicolor、virginica）

類別	precision（精確率）	recall（召回率）	f1-score（綜合分）	support（真實樣本數）	解讀
setosa	1.00	1.00	1.00	19	模型完美識別！預測為setosa的樣本，100%是真setosa；所有真實setosa也全被找出來了
versicolor	1.00	0.92	0.96	13	精確率滿分（預測versicolor的樣本都真），但召回率稍低（13個真實樣本中，1個被誤判）
virginica	0.93	1.00	0.96	13	召回率滿分（真實virginica全被找），但精確率稍低（預測virginica的樣本中，7%是誤判）

2.整體指標（accuracy、macro avg、weighted avg）

指標	數值	解讀
accuracy	0.98	整體準確率：45個測試樣本中，98%預測正確，僅1-2個樣本分類錯誤
macro avg	0.98/0.97/0.97	宏平均：綜合三類的精確率、召回率、F1，整體表現極佳
weighted avg	0.98/0.98/0.98	加權平均：因setosa表現極佳，拉高了整體分數，模型穩健

總體的表現性能很優秀，但有些地方還有一定的優化空間，下面給出一些優化方向。

1. 調整決策樹深度：
   當前 max_depth=3，若增至4，模型可能學習更細的邊界，區分開那2個誤判樣本。

2. 驗證測試集分布：
   測試集中 versicolor 和 virginica 這兩類樣本較少，若有更多樣本，模型表現會更穩定。

本小節，通過驗證結果可知模型整體表現優秀，setosa 完美識別，僅在 versicolor 和 virginica 的邊界樣本上有微小失誤。對于鳶尾花這種簡單數據集，當前決策樹的配置已經足夠了！

5 小結

本文是前文【機器學習-2】的進階，在前文中主要學習了決策樹的原理，在這里就用一個具體的項目來進行學習和更深入的理解，本文算是實踐篇。

在本次基于鳶尾花數據集的決策樹實驗中，模型表現優異。借助 scikit-learn 僅需數行代碼，即可完成從數據加載、訓練到可視化的全流程；通過分類報告可知，決策樹在測試集上準確率達 98%，且可視化決策樹清晰展現了花瓣長度、寬度等特征閾值如何驅動分類，模型邏輯直觀。

若追求更優效果，可從三方面迭代：一是調參探索（如調整 max_depth 平衡復雜度、修改 min_samples_split 控制節點分裂、切換 criterion 對比 entropy 與 gini 差異）；二是剪枝優化（通過預剪枝 / 后剪枝限制過擬合，如設置 ccp_alpha）；三是跨場景驗證，嘗試泰坦尼克生存預測、葡萄酒質量分類等真實數據集，檢驗決策樹在復雜業務中的泛化能力，進一步挖掘模型潛力。