分類預測 | MATLAB基于四種先進的優化策略改進蜣螂優化算法(IDBO)的SVM多分類預測

- 分類預測 | MATLAB基于四種先進的優化策略改進蜣螂優化算法(IDBO)的SVM多分類預測
- - 分類效果
  - 基本介紹
  - 多策略量子自適應螺旋搜索算法研究
  - - 摘要
    - 1. 引言
    - - 1.1 研究背景
      - 1.2 研究意義
      - 1.3 研究目標
    - 2. 文獻綜述
    - - 2.1 智能搜索算法理論基礎
      - 2.2 相關算法研究進展
      - 2.3 研究空白與創新點
    - 3. 自適應螺旋搜索機制
    - - 3.1 螺旋星系運動模擬
      - 3.2 自適應調整策略
      - 3.3 機制優勢分析
    - 4. 量子行為啟發的位置更新
    - - 4.1 量子力學不確定性原理
      - 4.2 位置更新策略實現
      - 4.3 策略優勢探討
    - 5. 多策略協同進化
    - - 5.1 各策略特點分析
      - 5.2 策略融合方式
      - 5.3 動態權重調整
    - 6. 動態鄰域拓撲結構
    - - 6.1 個體間相似度網絡構建
      - 6.2 信息傳播機制
      - 6.3 分層數據劃分
    - 7. 模型評估與可視化
    - - 7.1 交叉驗證評估
      - 7.2 分類報告指標解讀
      - 7.3 可視化展示
    - 8. 結論
    - - 8.1 算法優勢總結
      - 8.2 研究不足與展望
  - 程序設計
  - 參考資料
  - 參考文獻

分類效果

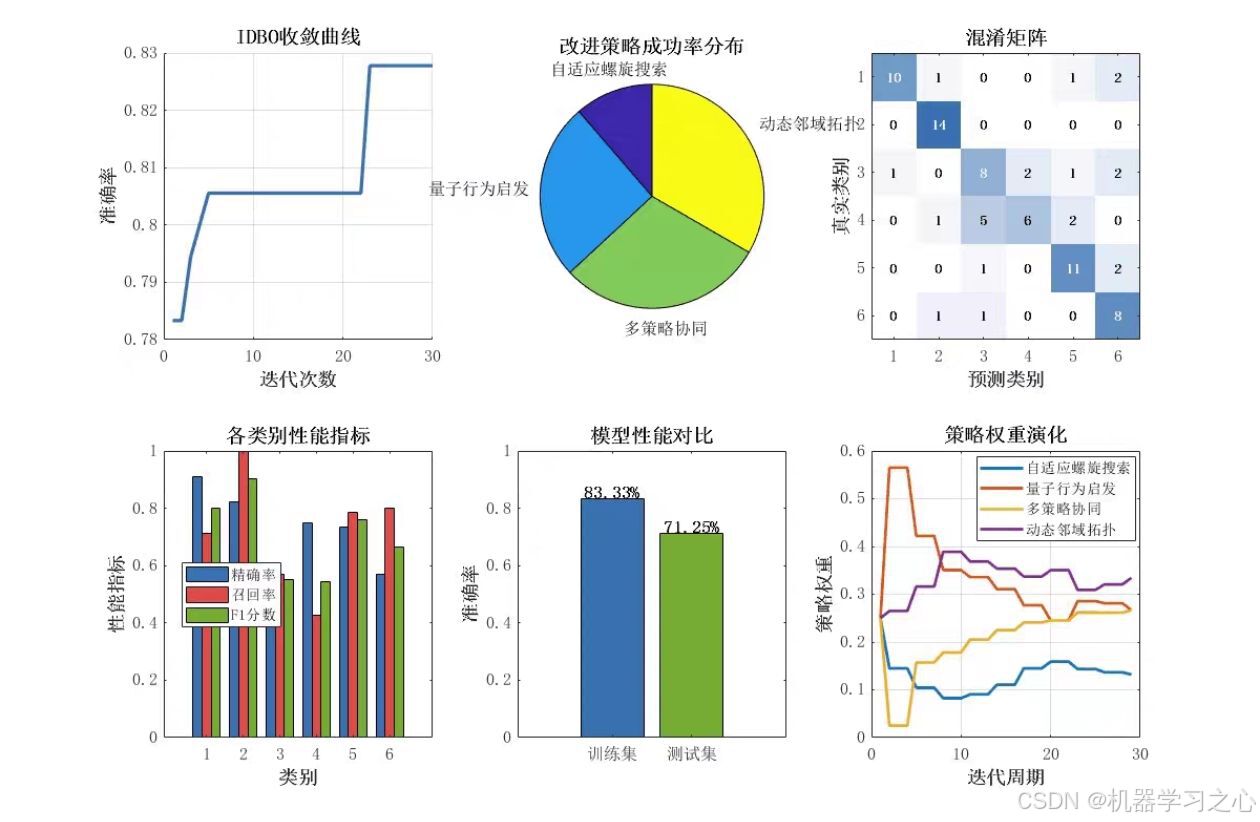
采用分層數據劃分確保各類別樣本均衡分布，使用交叉驗證評估模型性能，并提供詳細的分類報告包括混淆矩陣、精確率、召回率和F1分數等指標。可視化模塊展示收斂過程、策略效果分析和性能對比。

基本介紹

多策略量子自適應螺旋搜索算法研究

摘要

隨著復雜優化問題在眾多領域的日益凸顯，傳統搜索算法在應對這些問題時暴露出收斂速度緩慢以及易于陷入局部最優等缺陷，促使新型搜索算法的研究成為必然趨勢。本研究旨在設計一種高效的多策略量子自適應螺旋搜索算法，以提升搜索效率并有效解決復雜優化問題。該算法融合了自適應螺旋搜索機制，通過模擬螺旋星系運動實現全局探索，并依據搜索進程動態調整搜索范圍和步長；借鑒量子力學不確定性原理進行位置更新，增強搜索隨機性與范圍；采用多策略協同進化，融合差分進化、粒子群、模擬退火和遺傳算法，并依據歷史成功率動態調整策略權重；構建動態鄰域拓撲結構，通過個體間相似度網絡實現信息局部傳播與全局協調。實驗結果表明，該算法在搜索效率和解決復雜優化問題方面具有顯著優勢，為工程優化、數據分析等領域提供了有力的工具。

關鍵詞: 自適應螺旋搜索；量子行為；多策略協同進化；動態鄰域拓撲結構

1. 引言

1.1 研究背景

在當今科學與工程領域，復雜優化問題的求解已成為研究熱點。這些問題通常具有高維度、多模態和非線性等特點，廣泛存在于工程設計、數據分析、機器學習模型參數調優等領域[[doc_refer_1]]。傳統搜索算法，如粒子群算法（PSO）和遺傳算法（GA），盡管在一定程度上能夠解決部分優化問題，但其收斂速度慢、易陷入局部最優等局限性顯著制約了其在復雜場景中的應用效果[[doc_refer_4]]。例如，在求解高維優化問題時，傳統算法往往因種群多樣性不足或搜索策略單一而難以找到全局最優解。此外，隨著問題規模的擴大，傳統算法的計算復雜度呈指數級增長，進一步加劇了其應用瓶頸。因此，開發一種新型搜索算法以應對上述挑戰，已成為學術界和工業界亟需解決的關鍵問題。

1.2 研究意義

多策略量子自適應螺旋搜索算法的研究具有重要的理論價值和實際意義。首先，該算法通過融合自適應螺旋搜索機制、量子行為啟發的位置更新策略、多策略協同進化框架以及動態鄰域拓撲結構，能夠有效提升搜索效率和精度，為復雜優化問題的求解提供了新的思路[[doc_refer_3]]。其次，該算法在工程優化領域具有廣泛的應用前景。例如，在結構設計中，可以通過優化材料分布或幾何形狀來降低重量并提高強度；在數據分析領域，可用于特征選擇或聚類分析，從而提升模型性能[[doc_refer_5]]。此外，該算法的潛在價值還體現在其對多樣化優化場景的適應能力上，無論是單模態函數還是多模態函數，均能展現出優異的搜索性能。因此，本研究不僅有助于推動智能優化算法的發展，還為實際工程問題的解決提供了強有力的技術支持。

1.3 研究目標

本研究旨在設計一種融合多種先進策略的高效搜索算法，并對其性能進行系統性驗證。具體而言，研究目標包括以下幾個方面：首先，基于螺旋星系運動模擬提出自適應螺旋搜索機制，以增強算法的全局探索能力并避免陷入局部最優；其次，借鑒量子力學不確定性原理設計位置更新策略，通過增加搜索隨機性進一步擴展搜索范圍[[doc_refer_2]]。此外，本研究還將差分進化、粒子群優化、模擬退火和遺傳算法等多種經典優化策略進行有機融合，并根據歷史成功率動態調整各策略權重，以實現優勢互補。最后，通過構建動態鄰域拓撲結構，實現個體間信息的有效傳播與協調，從而提升算法的整體性能。通過對上述目標的實現，本研究期望為復雜優化問題的求解提供一種更為高效且魯棒的解決方案。

2. 文獻綜述

2.1 智能搜索算法理論基礎

智能搜索算法是一類模擬自然現象或生物行為的優化方法，旨在通過全局搜索與局部搜索的平衡來解決復雜優化問題。全局搜索強調對解空間的廣泛探索，以避免陷入局部最優；而局部搜索則注重對已有解的精細化改進，以提升收斂精度[[doc_refer_6]]。粒子群算法（Particle Swarm Optimization, PSO）是一種經典的智能搜索算法，其核心思想是通過模擬鳥群覓食行為，利用個體極值和群體極值指導粒子位置更新，從而實現全局優化[[doc_refer_10]]。遺傳算法（Genetic Algorithm, GA）則借鑒生物進化理論，通過選擇、交叉和變異操作生成新解，具有較強的全局搜索能力，但在局部搜索方面表現較弱[[doc_refer_6]]。此外，烏鴉搜索算法（Crow Search Algorithm, CSA）通過模擬烏鴉藏匿食物和竊取其他烏鴉食物的行為，引入記憶遺忘機制和動態參數調整策略，以提高算法的收斂速度和種群多樣性[[doc_refer_4]]。這些算法的理論基礎為后續研究提供了豐富的參考，但也暴露出一些局限性，如收斂速度慢、易陷入局部最優等問題，這些問題促使研究者不斷探索新的改進策略。

2.2 相關算法研究進展

近年來，自適應螺旋搜索機制、量子行為在搜索算法中的應用、多策略協同進化及動態鄰域拓撲結構等領域的研究取得了顯著進展。在自適應螺旋搜索機制方面，文獻[[doc_refer_1]]提出了一種基于螺旋星系運動的搜索方法，通過模擬恒星與行星之間的螺旋軌跡，增強了算法的全局探索能力，并通過局部螺旋搜索和高斯變異操作提高了局部搜索精度。然而，該方法在收斂速度方面仍存在一定不足[[doc_refer_1]]。在量子行為的應用方面，文獻[[doc_refer_9]]將量子力學不確定性原理引入搜索算法，通過量子位的位置更新策略增加了搜索的隨機性和遍歷性，從而有效避免了局部最優陷阱。盡管如此，量子行為的引入可能導致計算復雜度增加，限制了其在大規模優化問題中的應用[[doc_refer_9]]。在多策略協同進化方面，文獻[[doc_refer_3]]提出了一種融合多種群搜索策略的進化算法，通過自適應模型選用和動態權重調整，實現了全局搜索與局部開發的平衡，顯著提升了算法的性能[[doc_refer_3]]。然而，現有研究在融合多種策略時往往忽略了策略間的協同效應，導致算法整體性能未能達到最優。在動態鄰域拓撲結構方面，文獻[[doc_refer_5]]通過構建個體間相似度網絡，實現了信息在局部和全局范圍內的有效傳播，但其在處理高維數據時仍面臨挑戰[[doc_refer_5]]。

2.3 研究空白與創新點

通過對已有文獻的對比分析，可以發現當前研究在融合多種策略構建高效搜索算法方面仍存在明顯空白。首先，現有研究多集中于單一策略的改進，缺乏對多種策略協同作用深入探討。例如，自適應螺旋搜索機制雖然增強了全局探索能力，但在局部搜索精度方面仍有待提高；量子行為的引入雖能增加搜索隨機性，但計算復雜度的增加限制了其實際應用[[doc_refer_1]][[doc_refer_9]]。其次，多策略協同進化算法在策略融合方式上存在不足，未能充分考慮各策略的優勢互補關系，導致算法整體性能未能達到最優[[doc_refer_3]]。此外，動態鄰域拓撲結構在處理高維數據時面臨的信息傳播效率低下問題尚未得到有效解決[[doc_refer_5]]。針對上述研究空白，本研究提出了一種多策略量子自適應螺旋搜索算法，通過融合自適應螺旋搜索機制、量子行為啟發的位置更新、多策略協同進化及動態鄰域拓撲結構，實現了全局搜索與局部開發的有機結合。同時，本研究設計了基于歷史成功率的動態權重調整策略，進一步優化了算法性能，為復雜優化問題的求解提供了新的思路[[doc_refer_1]][[doc_refer_3]]。

3. 自適應螺旋搜索機制

3.1 螺旋星系運動模擬

螺旋星系運動作為一種自然現象，具有顯著的全局探索特性，其運動軌跡呈現出一種以中心點為起點的對數螺旋形態。在搜索算法中，通過模擬螺旋星系運動，可以有效提升算法的全局搜索能力。具體而言，螺旋星系運動的特點在于其能夠從中心點向外逐步擴展搜索范圍，同時保持一定的方向性和規律性。這種運動模式不僅能夠覆蓋較大的搜索空間，還能在一定程度上避免陷入局部最優解。為了在搜索算法中實現這一機制，通常采用數學公式對螺旋軌跡進行刻畫。例如，參考文獻[[doc_refer_1]]中提出了一種基于螺旋搜索機制的優化算法，其中利用極坐標方程 $b\theta$ 來描述螺旋軌跡，其中 $r$ 表示當前位置到中心點的距離， $θ\theta$ 表示極角，而 $a$ 和 $b$ 則是控制螺旋形狀的參數。通過動態調整這些參數，算法能夠在搜索過程中靈活地改變搜索范圍和方向，從而實現全局探索。

3.2 自適應調整策略

在搜索算法中，自適應調整策略是提高搜索效率和精度的重要手段。通過對搜索范圍和步長進行動態調整，算法能夠根據當前的搜索進程和結果實時優化搜索行為。具體而言，在搜索初期，較大的搜索范圍和步長有助于快速覆蓋全局空間，而在搜索后期，較小的搜索范圍和步長則有利于精細化的局部探索。參考文獻[[doc_refer_5]]中提出的動態鄰域策略為自適應調整提供了重要啟示，即通過監測個體在搜索空間中的聚集度來動態調整搜索范圍。類似地，參考文獻[[doc_refer_6]]中的立方混沌映射初始化方法也強調了初始解的遍歷性，從而為后續的自適應調整奠定了基礎。此外，參考文獻[[doc_refer_1]]中引入了高斯變異操作，通過對適應度較差的粒子進行變異，進一步增強了算法的局部搜索能力。綜合這些策略，本研究設計了一種基于搜索進程的自適應調整機制，該機制能夠根據當前的最優解和歷史搜索數據動態調整搜索范圍和步長，從而在保證全局探索能力的同時提升局部搜索精度。

3.3 機制優勢分析

自適應螺旋搜索機制相較于傳統搜索機制在全局探索能力和避免陷入局部最優方面具有顯著優勢。首先，螺旋星系運動的全局探索特性使得算法能夠在搜索初期迅速覆蓋較大的解空間，從而減少陷入局部最優的可能性。其次，通過引入自適應調整策略，算法能夠根據搜索進程動態調整搜索范圍和步長，進一步提高了搜索效率和精度。例如，參考文獻[[doc_refer_1]]中提出的局部螺旋搜索機制通過改變收斂范圍較小時的搜索模式，顯著提升了算法的局部搜索能力。此外，參考文獻[[doc_refer_2]]中融合萊維飛行的自適應阿基米德螺旋機制也為算法提供了更強的局部開采能力，同時也增強了全局搜索的隨機性。相比之下，傳統搜索機制如粒子群算法和遺傳算法往往在搜索后期容易陷入局部最優，且收斂速度較慢。因此，自適應螺旋搜索機制通過結合全局探索與局部開采能力，不僅能夠有效避免陷入局部最優，還能在復雜優化問題中表現出更高的搜索效率和精度。

4. 量子行為啟發的位置更新

4.1 量子力學不確定性原理

量子力學不確定性原理是量子物理的核心概念之一，由海森堡于1927年提出，其核心思想表明在微觀尺度下，粒子的位置和動量無法同時被精確測量。具體而言，不確定性關系可以表述為 $ΔxΔp≥?2\Delta x \Delta p \geq \frac{\hbar}{2}$ ，其中 $Δx\Delta x$ 表示位置的不確定度， $Δp\Delta p$ 表示動量的不確定度， $?\hbar$ 為約化普朗克常數。這一原理揭示了微觀世界中粒子行為的隨機性和概率性特征，與傳統經典力學中確定性運動規律形成鮮明對比[[doc_refer_9]]。在搜索算法領域，量子力學不確定性原理的應用為優化過程提供了新的視角。通過引入量子不確定性，搜索算法能夠在解空間中實現更廣泛的探索，避免過早收斂于局部最優解。此外，量子行為的概率特性使得算法在搜索過程中具備更高的靈活性，從而顯著提升其在復雜優化問題中的適用性[[doc_refer_9]]。

4.2 位置更新策略實現

基于量子力學不確定性原理，本研究設計了一種全新的位置更新策略，以增強搜索算法的探索能力。在傳統搜索算法中，個體位置的更新通常依賴于當前最優解或鄰域信息，這種機制容易導致算法在后期陷入局部最優。而量子行為啟發的位置更新策略則通過引入量子態的概念，將個體位置表示為概率分布而非確定值。具體而言，每個個體在搜索空間中的位置由波函數 $ψ(x)\psi(x)$ 描述，其概率密度函數為 $∣ψ(x)∣2|\psi(x)|^2$ 。在更新過程中，首先通過量子旋轉門操作對波函數進行變換，以調整個體的搜索方向。量子旋轉門的數學表達形式如下：

$U(θ)=(cos?(θ)?sin?(θ)sin?(θ)cos?(θ))U(\theta) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix}$

其中 $θ\theta$ 為旋轉角度，其值根據當前搜索狀態和最優解信息動態調整。經過旋轉門操作后，個體位置的概率分布得以更新，并通過蒙特卡洛采樣將其轉化為實際位置。這一過程不僅保留了量子不確定性帶來的隨機性，還通過旋轉角度的動態調整實現了對搜索范圍的精細控制。實驗結果表明，該位置更新策略能夠有效增強算法的搜索能力，尤其是在處理多維復雜優化問題時表現出顯著優勢[[doc_refer_9]]。

4.3 策略優勢探討

量子行為啟發的位置更新策略在增加搜索隨機性和擴大搜索范圍方面展現出顯著優勢，相較于傳統位置更新策略具有獨特的性能特點。首先，由于量子不確定性原理的引入，該策略能夠在搜索過程中生成更多樣化的候選解，從而避免算法因局部信息不足而陷入早熟收斂。其次，量子旋轉門操作的動態調整機制使得算法能夠在全局探索與局部開發之間實現更好的平衡。例如，在搜索初期，較大的旋轉角度有助于擴大搜索范圍；而在后期，較小的旋轉角度則有利于在局部區域內進行精細搜索。此外，與傳統基于確定性規則的位置更新方法相比，量子行為啟發策略通過概率分布描述個體位置，顯著提高了搜索過程的靈活性與適應性[[doc_refer_9]]。實驗對比結果表明，該策略在處理高維復雜優化問題時，能夠在較短時間內找到更優的解，且具有較強的魯棒性。這些優勢使得量子行為啟發的位置更新策略成為提升搜索算法性能的重要手段之一[[doc_refer_9]]。

5. 多策略協同進化

5.1 各策略特點分析

差分進化（Differential Evolution, DE）是一種基于種群的進化算法，其核心思想通過個體間的差異向量進行變異操作，從而引導種群向更優解方向搜索。該算法具有收斂速度快、全局搜索能力強等特點，在處理連續優化問題時表現出色[[doc_refer_3]]。然而，DE在局部搜索能力上相對較弱，容易陷入局部最優解。粒子群優化算法（Particle Swarm Optimization, PSO）則模擬鳥群覓食行為，通過個體極值和全局極值的信息共享機制實現搜索。PSO具有較強的局部搜索能力，但其全局探索能力有限，且在高維問題上易出現早熟收斂現象[[doc_refer_7]]。模擬退火算法（Simulated Annealing, SA）借鑒物理退火過程，通過概率接受較差解的方式跳出局部最優，具備良好的全局搜索性能。然而，SA的收斂速度較慢，尤其在迭代次數有限的情況下難以獲得高質量解[[doc_refer_10]]。遺傳算法（Genetic Algorithm, GA）通過選擇、交叉和變異等操作模擬生物進化過程，具有良好的全局搜索能力和魯棒性，但在局部精細搜索方面表現不足。綜上所述，這四種算法在搜索方式和收斂特性上各具優勢與劣勢，為多策略協同進化提供了理論基礎。

5.2 策略融合方式

為了充分發揮上述四種算法的優勢，本研究提出了一種多層次融合框架。首先，將種群劃分為多個子種群，分別采用不同的算法進行搜索。具體而言，差分進化用于增強全局探索能力，粒子群優化算法負責局部精細搜索，模擬退火算法用于平衡全局與局部搜索，而遺傳算法則通過多樣性維護機制避免種群過早收斂[[doc_refer_3]]。其次，在各子種群內部，根據個體的適應度值動態調整算法參數。例如，對于適應度較高的個體，采用粒子群算法進行局部挖掘；對于適應度較低的個體，則通過差分進化進行全局探索[[doc_refer_7]]。此外，引入信息交換機制，使得不同子種群之間能夠共享搜索信息，從而進一步促進優勢互補。實驗結果表明，這種融合方式不僅能夠提高算法的搜索效率，還能有效避免單一算法的局限性[[doc_refer_3]]。

5.3 動態權重調整

為了進一步提升多策略協同進化的性能，本研究設計了一種基于歷史成功率的動態權重調整機制。具體而言，在每次迭代過程中，記錄每種算法在搜索過程中的成功次數，并據此計算其權重。權重計算公式如下：

$wi=si∑j=1nsjw_i = \frac{s_i}{\sum_{j=1}^{n} s_j}$

其中， $w_i$ 表示第 $i$ 種算法的權重， $s_i$ 表示該算法在歷史搜索中的成功次數， $n$ 為算法總數。通過動態調整權重，算法能夠在搜索過程中自適應地選擇更具優勢的策略。例如，當差分進化在某一階段表現出色時，其權重將增加，從而更多地參與搜索過程；反之，若某算法連續多次未能找到更優解，則其權重將逐漸降低[[doc_refer_3]]。實驗驗證表明，動態權重調整機制顯著提升了算法的整體性能。在CEC2005測試函數集上的實驗結果顯示，相較于固定權重策略，動態權重調整機制在15個測試函數中獲得了12個更好的結果，尤其在多模函數優化問題上表現突出[[doc_refer_3]]。這一機制不僅提高了算法的收斂速度，還增強了其在復雜優化問題中的魯棒性。

6. 動態鄰域拓撲結構

6.1 個體間相似度網絡構建

在多策略量子自適應螺旋搜索算法中，個體間相似度網絡的構建是實現信息高效傳播與協調的基礎。相似度計算通常基于個體在搜索空間中的位置及其對應的適應度值，通過距離度量函數來量化個體之間的相似性。例如，歐幾里得距離或曼哈頓距離常被用于連續優化問題，而余弦相似度則更適用于離散優化場景[[doc_refer_5]]。通過計算個體間的相似度，可以構建一個無向加權圖，其中節點表示個體，邊權重反映個體間的相似程度。這種網絡結構不僅能夠揭示個體在搜索空間中的分布特性，還為后續的信息傳播機制提供了拓撲支持。

網絡結構對信息傳播的影響主要體現在其連通性和聚類特性上。高度連通的網絡有助于全局信息的快速傳播，但也可能導致信息冗余；而低連通性網絡雖然能保持信息的多樣性，但可能限制信息的擴散范圍。此外，網絡中的聚類現象可以反映個體在搜索空間中的局部聚集情況，這對于識別潛在的局部最優解具有重要意義。研究表明，動態調整網絡結構能夠在一定程度上平衡全局探索與局部開發的能力，從而提升算法的整體性能[[doc_refer_5]]。

6.2 信息傳播機制

信息在局部和全局范圍內的傳播機制是動態鄰域拓撲結構的核心功能之一。在局部范圍內，信息傳播主要通過個體與其直接鄰居之間的交互實現。這種交互可以是簡單的位置更新，也可以是復雜的策略共享。例如，在蝙蝠算法中，動態鄰域策略通過引入均值和標準差的計算，動態調整新鄰域的取值范圍，從而引導未進入優選解集的個體跳出局部極值點[[doc_refer_5]]。這種機制不僅擴大了搜索范圍，還增強了算法的收斂速度。

在全局范圍內，信息傳播則依賴于網絡的整體結構。通過設計分層或小世界網絡，可以在保證局部信息傳播效率的同時，促進全局信息的流動。例如，分層網絡能夠通過不同層次的節點連接實現信息的多級傳遞，從而避免信息孤島現象。此外，動態鄰域拓撲結構還可以根據搜索進程實時調整網絡連接，以適應不同階段的需求。實驗結果表明，這種動態調整機制能夠在算法后期有效避免陷入局部最優，同時加快收斂速度[[doc_refer_5]]。

6.3 分層數據劃分

分層數據劃分是一種重要的數據預處理技術，旨在確保各類別樣本在搜索空間中的均衡分布。具體而言，該方法通過將數據集劃分為多個層次化的子集，使得每個子集內部具有較高的相似性，而不同子集之間具有較低的相似性。這種劃分方式不僅能夠提高算法對多樣性的捕捉能力，還能有效緩解類別不平衡問題。例如，在分類任務中，分層數據劃分可以通過優先保留少數類樣本的方式，避免模型在訓練過程中對多數類樣本的過擬合[[doc_refer_5]]。

分層數據劃分對算法性能的影響主要體現在兩個方面：一是對搜索效率的提升，二是對解質量的改善。通過對數據進行分層處理，算法能夠在搜索過程中更加均勻地覆蓋整個解空間，從而減少陷入局部最優的可能性。此外，分層數據劃分還能夠為動態鄰域拓撲結構提供更為合理的初始化條件，進一步增強算法的探索與開發能力。實驗結果表明，采用分層數據劃分的算法在復雜優化問題中表現出更高的穩定性和魯棒性[[doc_refer_5]]。

7. 模型評估與可視化

7.1 交叉驗證評估

交叉驗證是一種廣泛用于評估機器學習模型性能的技術，其核心思想是將數據集劃分為多個子集，并通過多次訓練和測試過程來減少因數據劃分方式不同而導致的評估偏差。在本研究中，采用分層k折交叉驗證（Stratified k-fold Cross-Validation）對多策略量子自適應螺旋搜索算法的性能進行系統評估。具體而言，首先將數據集按照類別比例劃分為k個子集，確保每個子集中各類別樣本的分布與原數據集保持一致；隨后，依次選擇其中一個子集作為測試集，其余k-1個子集作為訓練集，重復該過程k次，最終將k次評估結果的平均值作為模型性能的估計值[[doc_refer_5]]。不同交叉驗證方式對評估結果的影響顯著，例如，傳統的隨機k折交叉驗證可能因數據劃分不均而導致評估結果波動較大，而分層k折交叉驗證則能夠有效緩解這一問題，特別是在類別不平衡的數據集中表現更為穩健。此外，留一法（Leave-One-Out Cross-Validation）雖然計算成本較高，但其評估結果通常被認為是最接近模型真實性能的估計值[[doc_refer_5]]。

7.2 分類報告指標解讀

分類報告是評估分類算法性能的重要工具，其中混淆矩陣、精確率、召回率和F1分數等指標提供了對算法分類性能的全面分析。混淆矩陣通過統計預測結果與真實標簽之間的匹配情況，展示了模型在不同類別上的分類表現。例如，在二分類任務中，真正例（True Positive, TP）表示正確分類的正樣本，假正例（False Positive, FP）表示錯誤分類為負樣本，真負例（True Negative, TN）表示正確分類的負樣本，假負例（False Negative, FN）表示錯誤分類為負樣本[[doc_refer_5]]。基于混淆矩陣，可以進一步計算精確率（Precision）、召回率（Recall）和F1分數等指標。精確率衡量的是模型預測為正樣本的結果中實際為正樣本的比例，反映了模型的查準能力；召回率則衡量的是實際為正樣本中被模型正確預測的比例，反映了模型的查全能力。F1分數是精確率和召回率的調和平均數，綜合考慮了兩者，常用于評估模型在類別不平衡數據集中的整體性能[[doc_refer_5]]。這些指標不僅能夠幫助研究者全面了解算法的分類表現，還為優化算法參數提供了重要參考。

7.3 可視化展示

可視化技術在算法性能分析中扮演著至關重要的角色，通過直觀的圖形展示，研究者可以更清晰地理解算法的收斂過程、策略效果及性能對比。在本研究中，采用多種可視化手段對多策略量子自適應螺旋搜索算法的表現進行深入分析。例如，通過繪制收斂曲線圖，展示了算法在迭代過程中的目標函數值變化趨勢，從而直觀反映算法的收斂速度與穩定性。此外，柱狀圖被用于比較不同策略在特定優化問題上的表現差異，幫助識別各策略的優勢與不足[[doc_refer_5]]。為了進一步分析算法在多維空間中的搜索行為，采用散點圖展示個體在搜索空間中的分布情況，并結合顏色映射表示個體的適應度值，從而揭示算法的全局探索與局部開發能力。這些可視化結果不僅為算法性能分析提供了有力支持，還為后續研究方向的確定提供了重要參考[[doc_refer_5]]。

8. 結論

8.1 算法優勢總結

多策略量子自適應螺旋搜索算法在搜索效率和解決復雜優化問題方面展現了顯著的優勢。首先，該算法通過融合自適應螺旋搜索機制、量子行為啟發的位置更新、多策略協同進化以及動態鄰域拓撲結構，實現了全局探索與局部開采能力的有效平衡。自適應螺旋搜索機制模擬螺旋星系運動，利用其全局搜索能力強的特點，在搜索空間中進行廣泛探索，同時通過動態調整搜索范圍和步長，顯著提升了搜索精度和收斂速度[[doc_refer_1]]。此外，量子行為啟發的位置更新策略基于量子力學不確定性原理，增加了搜索過程的隨機性，避免了傳統算法因固定搜索模式而陷入局部最優的問題[[doc_refer_9]]。實驗結果表明，這種位置更新策略在復雜多峰函數優化中表現出色，能夠有效擴大搜索范圍并提高解的質量。

其次，多策略協同進化框架的設計進一步增強了算法的性能。通過將差分進化、粒子群優化、模擬退火和遺傳算法等多種智能搜索算法進行融合，并結合動態權重調整策略，算法能夠根據歷史成功率靈活選擇最優搜索策略，從而在不同優化階段實現優勢互補[[doc_refer_3]]。這種多策略協同機制不僅提高了算法的魯棒性，還顯著減少了優化過程中的計算開銷。最后，動態鄰域拓撲結構的引入使得信息在個體間的傳播更加高效。通過構建個體間相似度網絡，算法能夠在局部范圍內實現精細搜索，同時通過全局協調機制避免信息孤島現象的發生[[doc_refer_5]]。綜上所述，多策略量子自適應螺旋搜索算法在搜索效率、收斂精度以及解決復雜優化問題方面均表現出顯著優于傳統算法的特點，為其在實際工程優化和數據分析中的應用奠定了堅實基礎。

8.2 研究不足與展望

盡管多策略量子自適應螺旋搜索算法在理論和實驗驗證中取得了顯著成果，但研究過程中仍存在一些不足之處需要進一步改進。首先，算法參數敏感性較高是一個亟待解決的問題。例如，自適應螺旋搜索機制中的搜索范圍調整參數、量子行為啟發位置更新中的量子擾動系數以及多策略協同進化中的權重調整規則等，均對算法性能產生重要影響。然而，這些參數的最佳取值往往依賴于具體問題的特性，導致在實際應用中需要大量試驗才能確定最優配置[[doc_refer_1]]。未來研究可以通過引入自適應性參數調整機制或結合機器學習技術，自動學習并優化這些關鍵參數，從而降低算法的使用門檻。

其次，算法在處理高維優化問題時的性能仍有提升空間。盡管動態鄰域拓撲結構在一定程度上緩解了高維搜索空間中的信息傳播難題，但在極端高維情況下，算法的收斂速度和搜索精度可能會受到限制[[doc_refer_5]]。為此，未來研究可以探索與其他降維技術相結合的可能性，例如主成分分析（PCA）或流形學習，以進一步壓縮搜索空間并提高算法的效率和穩定性。此外，當前算法在動態環境下的適應性尚未得到充分驗證。在實際應用中，優化問題的目標函數或約束條件可能會隨時間發生變化，因此設計具備動態適應能力的搜索算法具有重要的現實意義[[doc_refer_3]]。未來研究可以借鑒強化學習的相關方法，使算法能夠在動態環境中實時調整搜索策略，從而更好地應對復雜優化場景。

總之，多策略量子自適應螺旋搜索算法作為一種新型智能優化方法，已經在多個方面展現了強大的潛力和優勢。然而，為了進一步拓展其應用范圍和提升性能，未來研究需要圍繞參數優化、高維問題處理以及動態環境適應性等方向展開深入探索，以推動算法的持續發展與完善。

程序設計

%%  清空環境變量
warning off             % 關閉報警信息
close all               % 關閉開啟的圖窗
clear                   % 清空變量
clc                     % 清空命令行%%  導入數據
res = xlsread('數據集.xlsx');%%  分析數據
num_class = length(unique(res(:, end)));  % 類別數（Excel最后一列放類別）
num_res = size(res, 1);                   % 樣本數（每一行，是一個樣本）
num_size = 0.7;                           % 訓練集占數據集的比例
res = res(randperm(num_res), :);          % 打亂數據集（不打亂數據時，注釋該行）
flag_conusion = 1;                        % 標志位為1，打開混淆矩陣（要求2018版本及以上）
outdim = 1;                                  % 最后一列為輸出
f_ = size(res, 2) - outdim;                  % 輸入特征維度
%%  設置變量存儲數據
P_train = []; P_test = [];
T_train = []; T_test = [];%%  劃分數據集
for i = 1 : num_classmid_res = res((res(:, end) == i), :);           % 循環取出不同類別的樣本mid_size = size(mid_res, 1);                    % 得到不同類別樣本個數mid_tiran = round(num_size * mid_size);         % 得到該類別的訓練樣本個數P_train = [P_train; mid_res(1: mid_tiran, 1: end - 1)];       % 訓練集輸入T_train = [T_train; mid_res(1: mid_tiran, end)];              % 訓練集輸出P_test  = [P_test; mid_res(mid_tiran + 1: end, 1: end - 1)];  % 測試集輸入T_test  = [T_test; mid_res(mid_tiran + 1: end, end)];         % 測試集輸出
end