1 單選題（每題 2 分，共 30 分）

第1題 已知小寫字母 b 的ASCII碼為98，下列C++代碼的輸出結果是（?? ）。

1. #include <iostream>
2. using namespace std;
3. int main() {
4. ????char a = 'b' ^ 4;
5. ????cout << a;
6. ????return 0;
7. }

A. b????????????????????????????????????B. bbbb?????????????????????????????? C. f???????????????? ? ? ? ? ? ? ? ? ? ? ? D. 102

解析：答案C。'b?'為字符型，等人價整型98，'b' ^ 4等價98 ^ 4 = 0b01100010 ^ 0b00000100 = 0b01100110 = 102。char a表示a為字符型，102將轉換為字符'f'。????所以C.正確。故選C。

第2題 已知 a 為 int 類型變量， p 為 int * 類型變量，下列賦值語句不符合語法的是（?? ）。

A. *(p + a) = *p;???????????????? B. *(p - a) = a;??????????????????? C. p + a = p;???????????????????????? ? D. p = p + a;

解析：答案C。本題考察的是?指針運算的合法性?，關鍵點在于?指針變量是否可以用于賦值表達式的左側?。?A.?*(p + a) = *p;? ?合法?：*(p + a)?是對指針?p?偏移?a?后的地址解引用，并賦值?*p?的值，這是合法的指針運算和賦值操作。?B.?*(p - a) = a;? ?合法?：*(p - a)?是對指針?p?偏移?-a?后的地址解引用，并賦值為?a，這也是合法的指針運算和賦值操作。?C.?p + a = p;? ?非法：p + a?是一個?臨時計算的指針值(地址值)?，不能出現在賦值語句的左側（即不能作為左值），編譯器會報錯，因為表達式?p + a?的結果是?不可修改的臨時對象?。?D.?p = p + a;? ?合法?：對指針變量?p?進行偏移運算（p + a），并將結果賦值給?p，這是合法的指針運算和賦值操作。故選C。

第3題 下列關于C++類的說法，錯誤的是（?? ）。

A. 如需要使用基類的指針釋放派生類對象，基類的析構函數應聲明為虛析構函數。

B. 構造派生類對象時，只調用派生類的構造函數，不會調用基類的構造函數。

C. 基類和派生類分別實現了同一個虛函數，派生類對象仍能夠調用基類的該方法。

D. 如果函數形參為基類指針，調用時可以傳入派生類指針作為實參。

解析：答案B。若基類析構函數?未聲明為虛析構函數?，通過基類指針釋放派生類對象時會導致?內存泄漏?（僅調用基類析構函數，派生類部分未被釋放），?虛析構函數?確保多態性析構的正確調用，所以A.正確。?構造派生類對象時，會先調用基類構造函數，再調用派生類構造函數?，若基類未定義默認構造函數，派生類構造時必須顯式初始化基類，所以B.錯誤。派生類通過?base::?顯式調用基類虛函數（如?base::Method()），或通過基類指針/引用調用（覆蓋后仍可訪問基類實現），?基類指針可以指向派生類對象?（多態性），因此傳入派生類指針作為基類指針的實參是合法的，所以D.正確。故選B。

第4題 下列C++代碼的輸出是（?? ）。

1. #include <iostream>
2. using namespace std;
3. int main() {
4. ????int arr[5] = {2, 4, 6, 8, 10};
5. ????int * p = arr + 2;
6. ????cout << p[3] << endl;
7. ????return 0;
8. }

A. 6? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?B. 8

C. 編譯出錯，無法運行。??????????????????????????????????????? D. 不確定，可能發生運行時異常。

解析：答案D。arr是數組arr的首地址，即地址指向下標0，也就是元素2這個位置，int *p = arr + 2，指針p指向arr+2，即指向下標2，也就是元素6這個位置，這個位置相當于p[0]，所以p[3]已超arr的范圍，結果不確定，所以D.正確。故選D。

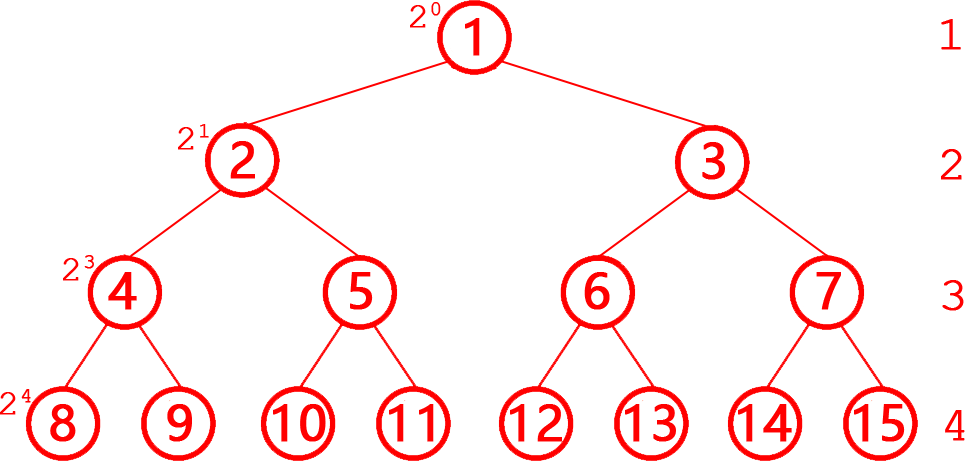
第5題 假定只有一個根節點的樹的深度為1，則一棵有N個節點的完全二叉樹，則樹的深度為（?? ）。

A. ?log?(N)?+1??????????????????? B. ?log?(N)????????????????????????? C. ?log?(N)?????????????????????????????? D. 不能確定

解析：答案A。完全二叉樹每行的第1個節點的編號=為2層號-1，層號=log?編號+1，對整層的其他節點：層號=?log?編號?+1，對最后一層就是深度(參考下圖)，所以對一棵有N個節點的完全二叉樹，如根節點的樹的深度為1，則樹的深度=?log?N?+1。故選A。

第6題 對于如下圖的二叉樹，說法正確的是（?? ）。

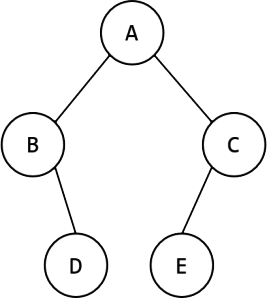
A. 先序遍歷是 ABDEC 。???????????????????????????????????????? B. 中序遍歷是 BDACE 。

C. 后序遍歷是 DBCEA 。???????????????????????????????????????? D. 廣度優先遍歷是 ABCDE 。

解析：答案D。先序遍歷是根-左樹-右樹，中序遍歷是左樹-根-右樹，后序遍歷是左樹-右樹-根，廣度優先遍歷是按層從上到下，每層從左到右。對本題圖中二叉樹：先序遍歷是ABDCE，A.錯誤；中序遍歷是BDAEC，B.錯誤；后序遍歷是DBECA，C.錯誤，廣度優先遍歷是ABCDE，D.正確。故選D。

第7題 圖的存儲和遍歷算法，下面說法錯誤的是（?? ）。

A. 圖的深度優先遍歷須要借助隊列來完成。

B. 圖的深度優先遍歷和廣度優先遍歷對有向圖和無向圖都適用。

C. 使用鄰接矩陣存儲一個包含𝑣個頂點的有向圖，統計其邊數的時間復雜度為𝑂(𝑣2)。

D. 同一個圖分別使用出邊鄰接表和入邊鄰接表存儲，其邊結點個數相同。

解析：答案A。深度優先遍歷（DFS）通常使用?棧?（遞歸或顯式棧）實現，而廣度優先遍歷（BFS）才需要隊列，所以A.錯誤。兩種遍歷算法均適用于有向圖和無向圖，僅訪問順序和實現細節可能不同，所以正確。包含𝑣個頂點的有向圖的鄰接矩陣需要遍歷整個𝑣×𝑣矩陣才能統計邊數，時間復雜度為 𝑂(𝑣2)，C.正確。無論出邊還是入邊鄰接表，每條邊均被存儲一次，僅方向不同，邊結點總數相同，D.正確。故選A。

第8題 一個連通的簡單有向圖，共有28條邊，則該圖至少有（?? ）個頂點。

A. 5 ???????????????????????????????????? B. 6?????????????????????????????????????? C. 7??????????????????????????????????????????? D. 8

解析：答案B。對于?連通的簡單有向圖?，若共有28條邊，其最少頂點數的計算邏輯如下：

?對于簡單有向圖，若頂點數為𝑛，則最大邊數為𝑛 (𝑛?1)（每個頂點與其他?𝑛?1?個頂點各有一條有向邊）。題目要求邊數28，需滿足𝑛 (𝑛?1)≥28，即𝑛2?𝑛?28 ≥ 0，解方程≈5.82，因此最小的𝑛 =6。驗證：當n=8時，8×7=56≥28；當n=7時，7×6=42≥28；n=6?時，6×5=30≥28；當n=5?時，5×4=20<28（不滿足）。因此，?最少需要6個頂點?才能容納28條邊且保持連通性。?連通性約束：連通有向圖需保證至少n?1?條邊（如生成樹結構），但題目邊數（28）遠大于此下限，故頂點數由邊數上限決定為6。故選B。

第9題 以下哪個方案不能合理解決或緩解哈希表沖突（?? ）。

A. 在每個哈希表項處，使用不同的哈希函數再建立一個哈希表，管理該表項的沖突元素。

B. 在每個哈希表項處，建立二叉排序樹，管理該表項的沖突元素。

C. 使用不同的哈希函數建立額外的哈希表，用來管理所有發生沖突的元素。

D. 覆蓋發生沖突的舊元素。

解析：答案D。在每個哈希表項處，用不同哈希函數再建一個哈希表管理沖突元素，但嵌套哈希表會顯著增加空間復雜度，且二次哈希函數的設計需保證不引發新的沖突，實現復雜，A.可以解決，但不算很理想。在每個哈希表項處建立二叉排序樹管理沖突元素，這是鏈地址法的優化變種，可提高查詢效率，B.可以解決。使用不同哈希函數建額外哈希表管理所有沖突元素，類似“再哈希法”，通過備用哈希函數分散沖突，是常見策略之一，可以解決。直接覆蓋沖突的舊元素，會導致數據丟失，違反哈希表完整性原則，無法解決沖突，所以D.不能解決。故選D。

第10題 以下關于動態規劃的說法中，錯誤的是（?? ）。

A. 動態規劃方法通常能夠列出遞推公式。

B. 動態規劃方法的時間復雜度通常為狀態的個數。

C. 動態規劃方法有遞推和遞歸兩種實現形式。

D. 對很多問題，遞推實現和遞歸實現動態規劃方法的時間復雜度相當。

解析：答案B。動態規劃的核心是通過遞推公式（狀態轉移方程）描述子問題與原問題的關系，所以A.正確。動態規劃的時間復雜度取決于?狀態數量?與?每個狀態的計算復雜度?，通常為O(狀態數×單狀態計算復雜度)，所以B.錯誤。?遞歸實現?（自頂向下）：通過記憶化存儲避免重復計算，如斐波那契數列的遞歸解法；?遞推實現?（自底向上）：通過迭代填充狀態表，如數塔問題的遞推解法，所以C.正確。兩種實現的時間復雜度通常相同，雖然遞歸會導致指數級別的時間復雜度，因為它會計算許多重復的子問題，但動態規劃會存儲子問題的結果，來降低復雜度，使其變成多項式級別，但遞歸可能因函數調用棧產生額外開銷，所以D.正確。故選B。

第11題 下面程序的輸出為（?? ）。

1. #include < iostream>
2. using namespace std;
3. int rec_fib[100];
4. int fib(int n) {
5. ????if (n <= 1)
6. ????????return n;
7. ????if (rec_fib[n] == 0)
8. ????????rec_fib[n] = fib(n - 1) + fib(n - 2);
9. ????return rec_fib[n];
10. }
11. int main() {
12. ????cout << fib(6) << endl;
13. ????return 0;
14. }

A. 8?????????????????????????????????????? B. 13???????????????????????????????????? C. 64????????????????????????????????????????? D. 結果是隨機的

解析：答案A。本題程序實現了一個?帶記憶化（Memoization）的遞歸斐波那契數列計算?。斐波那契數列定義?：fib(0) = 0，fib(1) = 1；fib(n) = fib(n-1) + fib(n-2)（當?n > 1）。

全局數組?rec_fib?用于存儲已計算的斐波那契數，避免重復遞歸調用。若?rec_fib[n]?未被計算過（初始為0），則遞歸計算并存儲結果。計算結果：?fib(6)=fib(5)+ fib(4)=5+3=8。

具體遞歸展開如下：

fib(6) → fib(5) + fib(4) → 5 + 3 = 8

? fib(5) → fib(4) + fib(3) → 3 + 2 = 5?

? fib(4) → fib(3) + fib(2) → 2 + 1 = 3?

??? fib(3) → fib(2) + fib(1) → 1 + 1 = 2?

????? fib(2) → fib(1) + fib(0) → 1 + 0 = 1?

所以A.正確。故選A。

第 12 題 下面程序的時間復雜度為（?? ）。

1. int rec_fib[MAX_N];
2. int fib(int n) {
3. ????if (n <= 1)
4. ????????return n;
5. ????if (rec_fib[n] == 0)
6. ????????rec_fib[n] = fib(n - 1) + fib(n - 2);
7. ????return rec_fib[n];
8. }

A. O(2?)??????????????????? ? ? ? ? B. O(𝜙?),? ? ? ? ? ? ?C. O(n2)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? D. O(n)

解析：答案D。本題程序使用了?記憶化遞歸（Memoization）?來計算斐波那契數列，rec_fib[n]?數組存儲已經計算過的斐波那契數，避免重復計算。

每個?fib(k)（k ∈ [0, n]）?僅計算一次?，后續直接查表返回，時間復雜度 ?O(1)?。

?計算?fib(n)?時，會依次計算?fib(n-1), fib(n-2), ..., fib(0)，每個值只計算一次。

總共需要 ?n 次計算?（線性增長），因此時間復雜度為 ?O(n)?。普通遞歸的時間復雜度是 ?O(2?)?，因為會重復計算大量子問題。記憶化優化后，遞歸樹退化成?線性計算鏈?，復雜度降為 ?O(n)?。普通遞歸時間復雜度為O(2?)（或更精確的O(𝜙?)，𝜙 = (√5 + 1)/2 ≈ 1.618），所以A.、B.錯誤。無O(n2)這種情況，C.錯誤。故選?D?。

第13題 下面 search 函數的平均時間復雜度為（?? ）。

1. int search(int n, int * p, int target) {
2. ????int low = 0, high = n;
3. ????while (low < high) {
4. ????????int middle = (low + high) / 2;
5. ????????if (target == p[middle]) {
6. ????????????return middle;
7. ????????} else if (target > p[middle]) {
8. ????????????low = middle + 1; }
9. ????????else {
10. ????????????high = middle;
11. ????????}
12. ????}
13. ????return -1;
14. }

A. O(n log(n))??????????? ? ? ? ?B. O(n)??????????????????????? ? ? ?C. O(log(n)?????????? ? ? ? ? ? ?? D. O(1)

解析：答案C。本題的?search?函數明顯是?二分查找（Binary Search）?算法，其平均時間復雜度為 ?O(log n)。每次循環將搜索范圍縮小一半(middle = (low + high)/2)，通過比較?target?與中間值決定向左或向右繼續搜索；若找到目標值則直接返回索引(第5-6行)，否則調整?low?或?high?縮小范圍(第7-11行)；每次迭代將數據規模?n減半，最壞情況下需迭代?log?n? 次才能確定結果。常見的分治排序算法、快速排序，其時間復雜度O(n log n)，所以A.錯誤。適用于線性遍歷時間復雜度為?O(log n)，而二分查找無需遍歷全部元素，所以B.錯誤。O(1)僅適用于哈希表等直接訪問操作，二分查找需多次比較，做不到O(1)，所以D.錯誤。故選C。

?第 14 題 下面程序的時間復雜度為（?? ）。

1. int primes[MAXP], num = 0;
2. bool isPrime[MAXN] = {false};
3. void sieve() {
4. ????for (int n = 2; n <= MAXN; n++) {
5. ????????if (!isPrime[n])
6. ????????????primes[num++] = n;
7. ????????for (int i = 0; i < num && n * primes[i] <= MAXN; i++) {
8. ????????????isPrime[n * primes[i]] = true;
9. ????????????if (n % primes[i] == 0)
10. ????????????????break;
11. ????????}
12. ????}
13. }

A. O(n)????????????? ??? ? ? ? ?B. O(n×log n)????????????????????? C. O(n×log log n?????? ? ? ? ? ? ? ? D. O(n2)

解析：答案A。本題的程序實現的是?線性篩法（歐拉篩）?，用于高效生成素數，其時間復雜度為 ?O(n)?（線性復雜度）。外層循環（第 4 行）遍歷每個數?n（從 2 到?MAXN）。若?n?未被標記為非素數（!isPrime[n]），則將其加入素數表?primes（第 5-6 行）。內層循環（第 7-11 行）用當前素數?primes[i]?標記合數?n * primes[i]，并在?n?能被?primes[i]?整除時提前終止（第 9-10 行），確保每個合數僅被標記一次。?每個合數僅被標記一次?：通過?if (n % primes[i] == 0) break?保證每個合數由其最小素因子標記，避免重復操作。雖然存在嵌套循環，但每個合數的標記操作均攤時間復雜度為 O(1)，總操作次數與?MAXN?成線性關系。?對比?埃拉托斯特尼篩法（普通篩）?：時間復雜度 O(n log log n)，存在重復標記。所以A.正確。故選A。

第15題 下列選項中，哪個不可能是下圖的廣度優先遍歷序列（?? ）。

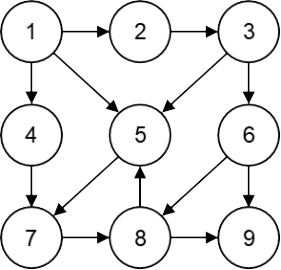
A. 1, 2, 4, 5, 3, 7, 6, 8, 9???????????????????????????????????????????????? B. 1, 2, 5, 4, 3, 7, 8, 6, 9

C. 1, 4, 5, 2, 7, 3, 8, 6, 9???????????????????????????????????????????????? D. 1, 5, 4, 2, 7, 3, 8, 6, 9

解析：答案B。根據廣度優先搜索（BFS）的特性，遍歷序列應按照層級順序逐層訪問節點，即從起始節點開始，先根節點入列，如有子節點(相鄰節點)，則所有子節點(相鄰節點)壓入隊列，依此類推，直到最后一個節點。對A.：先壓入①，再壓入①的相鄰節點②、④、⑤，接著壓入②的相鄰節點③(⑤已在隊列)、④的相鄰節點⑦、⑤的相鄰節點無(⑦已在隊列)，壓入③的相鄰節點⑥(⑤已在隊列)、⑦的相鄰節點⑧，最后是⑥的相鄰節點⑨。所以廣度優先遍歷序列1,2,4,5,3,7,6,8,9，所以A.正確。對B.：先壓入①，再壓入①的相鄰節點無②、⑤、④，接著壓入②的相鄰節點③(⑤已在隊列)、⑤的相鄰節點⑦、④的相鄰節點無(⑦已在隊列)，壓入③的相鄰節點⑥(⑤已在隊列)、⑦的相鄰節點⑧，最后是⑥的相鄰節點⑨。所以廣度優先遍歷序列1,2,5,4,3,7,6,8,9，不可能出現1, 2, 5, 4, 3, 7, 8, 6, 9，8到達不了6，所以B.錯誤。對C.：先壓入①，再壓入①的相鄰節點無④、⑤、②，接著壓入④的相鄰節點⑦、⑤的相鄰節點無(⑦已在隊列)、②的相鄰節點③，壓入⑦的相鄰節點⑧、③的相鄰節點⑥(⑤已在隊列)，最后是⑧的相鄰節點⑨。所以廣度優先遍歷序列1,4,5,2,7,3,8,6,9，所以C.正確。對D.：先壓入①，再壓入①的相鄰節點無⑤、④、②，接著壓入⑤的相鄰節點⑦、④的相鄰節點無(⑦已在隊列)、②的相鄰節點③，壓入⑦的相鄰節點⑧、③的相鄰節點⑥(⑤已在隊列)，最后是⑧的相鄰節點⑨。所以廣度優先遍歷序列1,5,4,2,7,3,8,6,9，所以C.正確。故選B。

2 判斷題（每題 2 分，共 20 分）

第1題 C++語言中，表達式 9 & 12 的結果類型為 int 、值為 8 。（?? ）

解析：答案正確。9 & 12 = 0b00001001 & 0b00001100 = 0b00001000 = 8。故正確。

第2題 C++語言中，指針變量指向的內存地址不一定都能夠合法訪問。（?? ）

?解析：答案正確。在C++中，指針變量可以指向任意內存地址，但并非所有地址都能被程序合法訪問。如：?未初始化的指針?：指向隨機內存地址，訪問可能導致崩潰或數據損壞。?已釋放的內存（野指針）?：訪問delete或free后的內存屬于未定義行為。?空指針（NULL或nullptr）?：解引用空指針會直接引發段錯誤。?越界訪問?：如數組越界或緩沖區溢出，可能破壞其他數據。?系統保護區域?：嘗試訪問操作系統保留地址（如0x00000000）會觸發硬件異常。故正確。

第3題 對𝑛個元素的數組進行快速排序，最差情況的時間復雜度為𝑂(𝑛 log 𝑛)。（?? ）

解析：答案錯誤。快速排序的最差時間復雜度為𝑂(𝑛2)，而非𝑂(𝑛 log 𝑛)。故錯誤。

第4題 一般情況下， long long 類型占用的字節數比 float 類型多。（?? ）

?解析：答案正確?。在大多數系統中，long long類型占用?8字節?，而float類型占用?4字節。long long類型，固定為8字節（64位），用于存儲大范圍整數（如?2?3 ~ 2?3?1）。?float類型?

固定為4字節（32位），采用IEEE 754浮點標準存儲，范圍約為±3.4×103?，但精度有限（約6~7位有效數字）。所以一般情況下long long類型占用的字節數比float類型多。故正確。

第5題 使用math.h或cmath頭文件中的函數，表達式pow(10, 3)的結果的值為1000、類型為int。（?? ）

解析：答案錯誤。在C++中，pow(10, 3)?的結果是10的3次冪，即?1000?（103）。

?pow()函數原型?：double pow(double base, double exponent);

參數和返回值均為double類型，但整數參數（如10和3）會隱式轉換為double計算，所以實際輸出通常為1000.0，類型為double。故錯誤。

第6題 二叉排序樹的中序遍歷序列一定是有序的。（?? ）

解析：答案正確。二叉排序樹的定義?：左子樹的所有節點值 ?小于? 當前節點值。右子樹的所有節點值 ?大于? 當前節點值。如下圖所示。

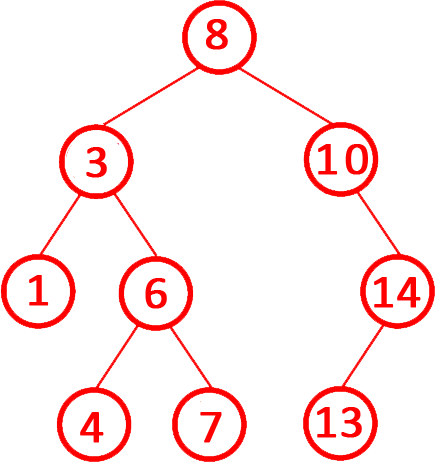
?中序遍歷（左-根-右）的特性?：先遍歷左子樹（所有值更小），再訪問根節點，最后遍歷右子樹（所有值更大）。因此，中序遍歷結果必然按?升序排列。故正確。

第7題 無論哈希表采用何種方式解決沖突，只要管理的元素足夠多，都無法避免沖突。（?? ）

解析：答案正確。哈希函數將較大的輸入空間映射到有限的輸出空間（哈希表大小），根據鴿巢原理，當元素數量超過哈希表容量時，必然存在多個元素映射到同一位置，即沖突不可避免。即使采用鏈地址法或開放尋址法等策略，沖突僅被緩解或分散，無法從根本上消除。故正確。

第8題 在C++語言中，類的構造函數和析構函數均可以聲明為虛函數。（?? ）

解析：答案錯誤。?在C++中，構造函數不能是虛函數?，因為虛函數依賴虛函數表（vtable）實現，而虛函數表在對象構造期間才被初始化。調用構造函數時，對象尚未完全創建，此時無法通過虛函數機制動態綁定。語法上，C++直接禁止構造函數聲明為virtual（編譯報錯）。?析構函數可以（且有時必須）是虛函數，其作用是當基類指針指向派生類對象時，若基類析構函數非虛，則通過該指針刪除對象會導致?派生類析構未被調用?，引發資源泄漏。故錯誤。

第9題 動態規劃方法將原問題分解為一個或多個相似的子問題，因此必須使用遞歸實現。（?? ）

解析：答案錯誤。?動態規劃（Dynamic Programming, DP）的核心思想是通過將原問題分解為?重疊子問題?，并存儲子問題的解（記憶化）來避免重復計算，從而提高效率。?關鍵點?：子問題必須具有?重疊性?和?最優子結構?，但實現方式不限定于遞歸。?動態規劃的兩種實現方式?：?自頂向下（遞歸+記憶化）?：使用遞歸分解問題，并通過哈希表或數組緩存子問題的解（即“記憶化搜索”）。?自底向上（迭代）?：從最小子問題開始，通過迭代逐步構建更大問題的解（通常用數組或表格存儲狀態）。?遞歸并非必需?。故錯誤。

第10題 如果將城市視作頂點，公路視作邊，將城際公路網絡抽象為簡單圖，可以滿足城市間的車道級導航需求。（?? ）

解析：答案錯誤。?將城市抽象為頂點、公路抽象為邊的簡單圖模型（無向、無權、無自環/重邊）無法精確表達車道級導航所需的細節，這是簡單圖的局限性?。車道級導航需包含?車道數量、轉向限制、實時交通狀態?等屬性，而簡單圖僅能表示城市間的連通性。?車道級導航的數據需求?：高精度導航依賴?動態權重?（如實時車速）、?車道級拓撲?（如出口車道標識）和?三維空間關系?（如高架橋分層），這些無法通過簡單圖的邊和頂點直接建模。故錯誤。

3 編程題（每題 25 分，共 50 分）

3.1 編程題1

• 試題名稱：線圖
• 時間限制：1.0 s
• 內存限制：512.0 MB

3.1.1 題目描述

給定由𝑛個結點與𝑚條邊構成的簡單無向圖𝐺，結點依次以1,2,...,𝑛編號。簡單無向圖意味著 中不包含重邊與自環。𝐺的線圖𝐿(𝐺)通過以下方式構建：

初始時線圖𝐿(𝐺)為空。

對于無向圖𝐺中的一條邊，在線圖𝐺中加入與之對應的一個結點。

對于無向圖𝐺中兩條不同的邊(𝑢?,𝑣?),(𝑢?,𝑣?)，若存在𝐺中的結點同時連接這兩條邊（即𝑢?,𝑣?之一與𝑢?,𝑣?之一相同），則在線圖𝐿(𝐺)中加入一條無向邊，連接(𝑢?,𝑣?),(𝑢?,𝑣?)在線圖中對應的結點。

請你求出線圖𝐿(𝐺)中所包含的無向邊的數量。

3.1.2 輸入格式

第一行，兩個正整數𝑛,𝑚，分別表示無向圖𝐺中的結點數與邊數。

接下來𝑚行，每行兩個正整數𝑢?,𝑣?，表示𝐺中連接𝑢?,𝑣?的一條無向邊。

3.1.3 輸出格式

輸出共一行，一個整數，表示線圖𝐿(𝐺)中所包含的無向邊的數量。

3.1.4 樣例

3.1.4.1 輸入樣例1

1. 5 4
2. 1 2
3. 2 3
4. 3 1
5. 4 5

3.1.4.2 輸出樣例1

1. 3

3.1.4.3 輸入樣例2

1. 5 10
2. 1 2
3. 1 3
4. 1 4
5. 1 5
6. 2 3
7. 2 4
8. 2 5
9. 3 4
10. 3 5
11. 4 5

3.1.4.4 輸出樣例2

1. 30

3.1.4.5 樣例解釋

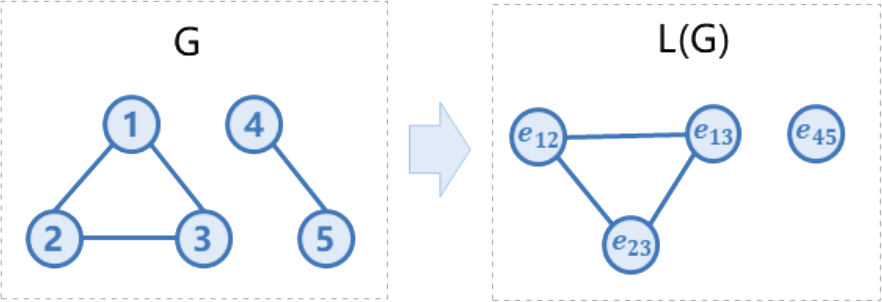
3.1.5 數據范圍

對于60%的測試點，保證1≤𝑛≤500，1≤𝑚≤500。 對于所有測試點，保證1≤𝑛≤10?，1≤𝑚≤10?。

3.1.6 編寫程序思路

分析：設計思路與原理：?線圖定義：線圖L(G)?的頂點對應原圖G?的邊。若原圖G?中兩條邊共享一個公共頂點，則在線圖L(G)?中對應的頂點之間連一條邊。線圖的邊數等于原圖中所有共享公共頂點的邊對數。對于原圖的每個頂點u，其鄰接邊的數量為edge(u)，貢獻的邊對數為?。構建鄰接表，記錄每個頂點的鄰接邊。遍歷每個頂點，計算其鄰接邊的組合數并累加。?時間復雜度?：鄰接表構建：O(m)，組合數計算：O(n)，總復雜度：O(n+m)。因為n≤10?，m≤10?，總復雜度在10?數量級，不會超時。完整參考程序代碼如下：

#include <iostream>
using namespace std;const int MaxN = 1e5+10; //頂點編號n≤10?
int n, m, edge[MaxN];??? //頂點編號1~n，初始為0int main() {cin >> n >> m;for (int i = 1; i <= m; ++i) { //輸入m條邊u?,v?int u, v;cin >> u >> v;edge[u]++;? //頂點計數edge[v]++;? //頂點計數}long long edge_count = 0;? //防止大數溢出for (int u = 1; u <= n; ++u)edge_count += 1ll * edge[u] * (edge[u] - 1) / 2; //組合運算cout << edge_count << endl;return 0;
}

3.2 編程題2

• 試題名稱：調味平衡
• 時間限制：1.0 s
• 內存限制：512.0 MB

3.2.1 題目描述

小A準備了𝑛種食材用來制作料理，這些食材依次以1,2,...,𝑛編號，第i種食材的酸度為a?，甜度為b?。對于每種食材，小A可以選擇將其放入料理，或者不放入料理。料理的酸度𝐴為放入食材的酸度之和，甜度𝐵為放入食材的甜度之和。如果料理的酸度與甜度相等，那么料理的調味是平衡的。 過于清淡的料理并不好吃，因此小A想在滿足料理調味平衡的前提下，合理選擇食材，最大化料理的酸度與甜度之和。你能幫他求出在調味平衡的前提下，料理酸度與甜度之和的最大值嗎？

3.2.2 輸入格式

第一行，一個正整數𝑛，表示食材種類數量。

接下來𝑛行，每行兩個正整數a?, b?，表示食材的酸度與甜度。

3.2.3 輸出格式

輸出共一行，一個整數，表示在調味平衡的前提下，料理酸度與甜度之和的最大值。

3.2.4 樣例

3.2.4.1 輸入樣例1

1. 3
2. 1 2
3. 2 4
4. 3 2

3.2.4.2 輸出樣例1

1. 8

3.2.4.3 輸入樣例2

1. 5
2. 1 1
3. 2 3
4. 6 1
5. 8 2
6. 5 7

3.2.4.4 輸出樣例2

1. 2

3.2.5 數據范圍

對于40%的測試點，保證1≤𝑛≤10，1≤a?, b?≤10。

對于另外20%的測試點，保證1≤𝑛≤50，1≤a?, b?≤10。

對于所有測試點，保證1≤𝑛≤100，1≤a?, b?≤500。

3.2.6 編寫程序思路

方法一：用vector(可變數組存放料理酸度與甜度， 不會vector也可用結構體struct)。需要選擇若干食材，使得它們的總酸度等于總甜度（A = B），同時最大化A + B（即2A或2B）。

這是一個典型的?動態規劃?問題，可以轉化為?背包問題?的變種：我們需要跟蹤酸度和甜度的差值（A - B），并記錄對應的最大總和（A + B）。用?動態規劃設計，?狀態定義?：dp[d]?表示酸度與甜度之差為?d?時的最大總和（A + B）。?初始化?：dp[0] = 0（差值為0時總和為0），其他狀態初始化為負無窮（表示不可達）。?狀態轉移?：對于每個食材，更新所有可能的差值?d：

如果選擇該食材，新的差值為?d + (a? - b?)，新的總和為?dp[d] + a? + b?。不選擇則保持原狀態。偏移量處理?：由于差值可能為負，使用偏移量將差值映射到非負范圍。?復雜度優化?，使用滾動數組或一維數組優化空間復雜度。差值范圍限制在?[-sum(a? + b?), sum(a? + b?)]?內，避免無效計算。時間復雜度O(n*MAX_DIFF)=100*105*505*2≈10?，不會超時。完整參考程序代碼如下：

#include?<iostream>
#include?<vector>
using?namespace?std;const?int?MAX_DIFF?=?105?*?505?*?2;?//n*a*2，最大可能差值范圍
const?int?OFFSET?=?MAX_DIFF?/?2;????//偏移量處理負值(中心點)int?main()?{ios::sync_with_stdio(false);?//即取消緩沖區同步，cin、cout效率接近scanf、printfcin.tie(nullptr);????????????//解除cin和cout之間的綁定，進一步加快執行效率int?n;cin?>>?n;vector<pair<int,?int?>>?items(n);?//pair成對數據.first存酸度a、.second存甜度bfor?(int?i?=?0;?i?<?n;?++i)?{cin?>>?items[i].first?>>?items[i].second;?//輸入n個酸度、甜度對}vector<int>?dp(MAX_DIFF?+?1,?-1000);?//1≤a?,b?≤500。a?-b?≥-499dp[OFFSET]?=?0;?//?初始狀態：差值為0時和為0for?(const?auto&?item?:?items)?{int?a?=?item.first,?b?=?item.second;int?diff?=?a?-?b;vector<int>?new_dp?=?dp;?//拷貝創建new_dp，dp的所有元素復制到new_dpfor?(int?j?=?0;?j?<=?MAX_DIFF;?++j)?{if?(dp[j]?!=?-1000)?{int?new_j?=?j?+?diff;if?(new_j?>=?0?&&?new_j?<=?MAX_DIFF)?{if?(new_dp[new_j]?<?dp[j]?+?a?+?b)?{new_dp[new_j]?=?dp[j]?+?a?+?b;}}}}dp?=?move(new_dp);?//資源所有權的轉移給dp，new_dp.size()=0}cout?<<?max(0,?dp[OFFSET])?<<?endl;return?0;
}

方法二：用一個動態規劃算法，主要功能是處理輸入數據并計算特定條件下的最大值。數組dp[MAX_DIFF+1]初始化為極小值(-16843010<-499)，僅dp[OFFSET]初始化為0，作為動態規劃的起點。核心算法：先讀取n對整數(a,b)，計算addt=a+b和subt=a-b?，根據subt值的正負采用不同的遍歷方向：subt≤0時正向遍歷更新dp數組，subt>0時逆向遍歷更新dp數組，通過max(dp[j+subt], dp[j]+addt)實現狀態轉移，記錄最大值，?輸出結果為最終輸出dp[OFFSET]的值，即中心位置的計算結果?。使用動態規劃思想，通過狀態轉移方程更新數組值?；采用雙指針技巧處理不同方向的遍歷需求。時間復雜度O(n*n*a*2)=100*105*505*2?≈10?，不會超時。完整參考程序代碼如下：

?#include <iostream>
#include <cstring> //含memset()函數
using namespace std;const int MAX_DIFF = 105 * 505 * 2; //n*a*2，最大可能差值范圍
const int OFFSET = MAX_DIFF / 2;??? //偏移量處理負值(中心點)int main() {ios::sync_with_stdio(false); //即取消緩沖區同步，cin、cout效率接近scanf、printfcin.tie(nullptr);??????????? //解除cin和cout之間的綁定，進一步加快執行效率int n;cin >> n;int dp[MAX_DIFF + 1]; //1≤a?,b?≤500。a?-b?≥-499memset(dp, -2, sizeof(dp)); //初始化為-16843010。0b11111110111111101111111011111110dp[OFFSET] = 0; // 初始狀態：差值為0時和為0for (int i = 0; i < n; ++i) {int a, b;cin >> a >> b;????????????????? //輸入n個數據對int addt = a + b, sunt = a - b; //求和及差if (sunt <= 0)?? //小于等于0，正向遍歷for (int j = -sunt; j <= MAX_DIFF; ++j)dp[j + sunt] = max(dp[j + sunt], dp[j] + addt);else???????????? //否則大于0，逆向遍歷for (int j = MAX_DIFF - sunt - 1; j; j--)dp[j + sunt] = max(dp[j + sunt], dp[j] + addt);}cout << max(0, dp[OFFSET]) << endl;return 0;
}