在學習數據結構之前,有些知識是很有必要提前知道的,它們包括:集合框架、復雜度和泛型。本篇文章專門介紹這三個東西。
1.集合框架
1.1 什么是集合框架
Java 集合框架(Java Collection Framework),又被稱為容器,是定義在 java.util 包下的一組接口 和 其實現類。其主要表現為將多個元素置于一個單元中,用與對這些元素進行快速、便捷的存儲、檢索、管理,即我們平時俗稱的增刪查改。
以下是Java集合框架的完整體系圖,梳理了集合框架中比較重要的接口、抽象類與具體的類的繼承/實現關系。
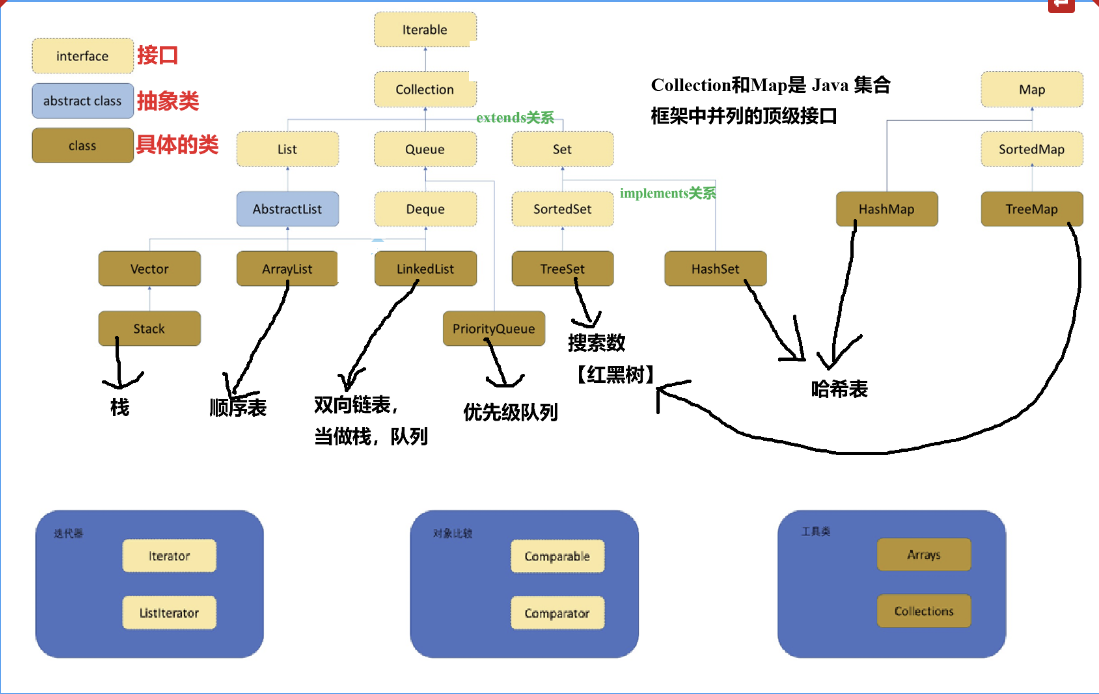
?1.2 集合框架的重要性
- 使用成熟的集合框架,有助于我們便捷、快速的寫出高效、穩定的代碼。
- 學習背后的數據結構知識,有助于我們理解各個集合的優缺點及使用場景。
?1.3 數據結構以及算法
1.3.1 什么是數據結構
數據結構(Data Structure)是計算機存儲、組織數據的方式,指相互之間存在一種或多種特定關系的數據元素的集合。
關于數據結構的一些問答:
1.Java的數據結構與C語言的數據結構有區別嗎?
“沒有”區別,只不過是實現的語言不一樣。
2.數據結構和數據庫是一個東西嗎?
有區別的,數據庫其實是用來儲存數據的,數據庫在儲存數據的時候,底層會用到數據結構。
3.數據結構怎么樣才能學好?
多思考,多畫圖,多寫代碼,多去調試。
1.3.2 什么是算法
算法(Algorithm):就是定義良好的計算過程,他取一個或一組的值為輸入,并產生出一個或一組值作為輸出。簡單來說算法就是一系列的計算步驟,用來將輸入數據轉化成輸出結果。
如何學好算法呢?
死磕代碼,注意畫圖和思考,多寫博客總結和多刷題。
另外,數據結構與算法相輔相成!
2.復雜度
知道了什么是算法,那么如何去衡量一個算法的好壞呢?這就引出了新概念——算法效率。
2.1 算法效率
算法效率分析分為兩種:第一種是時間效率,第二種是空間效率。時間效率被稱為時間復雜度,而空間效率被稱作空間復雜度。 時間復雜度主要衡量的是一個算法的運行速度,而空間復雜度主要衡量一個算法所需要的額外空間,在計算機發展的早期,計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展,計算機的存儲容量已經達到了很高的程度。所以我們如今已經不需要再特別關注一個算法的空間復雜度。
2.2 時間復雜度
2.2.1 時間復雜度的概念
時間復雜度的定義:在計算機科學中,算法的時間復雜度是一個數學函數,它定量描述了該算法的運行時間。一個 算法執行所耗費的時間,從理論上說,是不能算出來的,只有你把你的程序放在機器上跑起來,才能知道。但是我們需要每個算法都上機測試嗎?是可以都上機測試,但是這很麻煩,所以才有了時間復雜度這個分析方式。一個算法所花費的時間與其中語句的執行次數成正比例,算法中的基本操作的執行次數,為算法的時間復雜度。
可以舉個例子,現有一函數:
public void func(int N) {int count = 0;for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++;}}for (int i = 0; i < 2*N; i++) {count++;}int m = 10;while ((m--) > 0) {count++;}System.out.println(count);}結合時間復雜度的概念及這個函數,可以得出 func執行的基本操作次數為:
F(N) = N^2 + 2*N + 10
2.2.2? 大o的漸進表示法
實際中我們計算時間復雜度時,我們其實并不一定要計算精確的執行次數,而只需要大概執行次數,那么這里我們使用大O的漸進表示法。
大O符號(Big O notation):是用于描述函數漸進行為的數學符號。
大o的漸進表示法的規則:
- 用常數1取代運行時間中的所有加法常數。
- 在修改后的運行次數函數中,只保留最高階項。
- 如果最高階項存在且不是1,則去除與這個項目相乘的常數。得到的結果就是大O階。
那么使用大o的漸進表示法,上述函數 func 的時間復雜度為:
O(N^2)
大o的漸進表示法去掉了那些對結果影響不大的項,簡潔明了的表示出了執行次數。
另外,算法的時間復雜度還存在著最好、平均和最壞情況:
最好情況:任意輸入規模的最小運行次數(下界)。
平均情況:所有可能的輸入下,算法執行所需時間的平均度量。
最壞情況:任意輸入規模的最大運行次數(上界)
在實際中一般情況下,關注的是算法的最壞運行情況。
2.2.3?常見的時間復雜度計算舉例
1.冒泡排序
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}這個方法基本操作在最好情況下會執行N次,即一開始這個這個數組就已經排好序了,最壞情況下:數組完全逆序排列,那么第一輪需要操作 n-1次,第二輪需要操作 n-2次,第三輪需要操作 n-3次,……,最后一輪需要操作 1次,那么合起來就是:(n-1) + (n-2) + …… + 1 = (n-1)*n/2,用大o漸進表示法,得:O(N^2)。
2.二分查找
int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;}
這個方法的基本操作在最好情況下執行1次,即目標值剛好在中間,最壞情況:一直找,直到不滿足循環條件。因為每一輪查找都會使循環區間減半,即令初始區間長度為n,第一輪之后,區間長度變為 n/2,第二輪之后,n/4,……,第k輪后,n/(2*k),此時需要繼續縮小區間,直到區間為0,即?n/(2*k) <= 1,那么有 k 約等于 n以2為底的對數,使用大o的漸進表示法,得:O(n以2為底的對數)。
3.一般遞歸
long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;}像這種一般遞歸的方法, 通常它的時間復雜度 = 遞歸的次數 * 每次遞歸執行的次數。像這個方法,它的時間復雜度 = (N - 1)* 1 = N - 1,使用大o的漸進表示法,得:O(N)。
4.斐波那契數列的遞歸
int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}?用遞歸求斐波那契數列的方法不能看出一般的遞歸方法,因為當它在計算 fibonacci(N)時,這個方法又會調用 fibonacci(N - 1)和 fibonacci(N-2),這兩個子問題又會各自調用更小規模的子問題,形成一個類似二叉樹的調用結構:
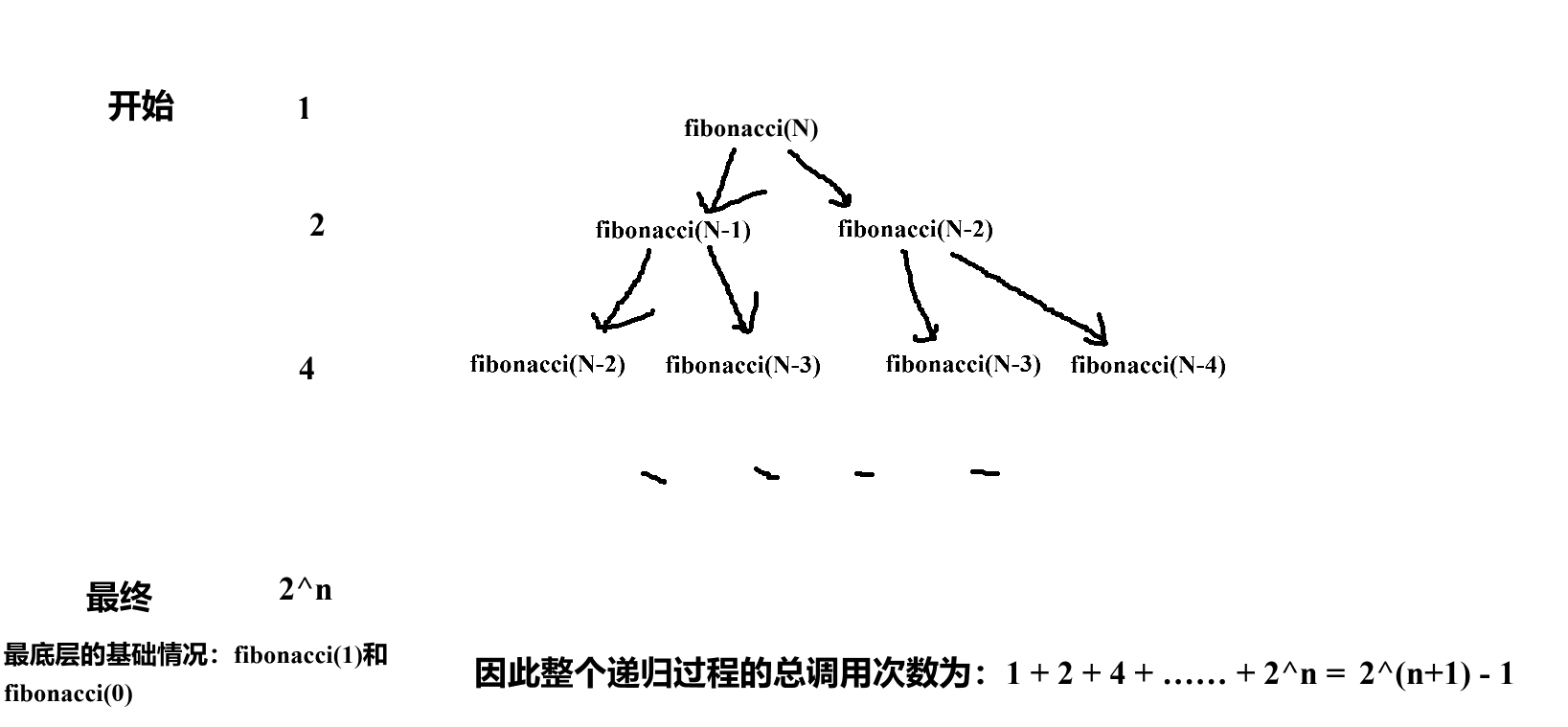
使用大o的漸進表示法,得:O(2^n)。
?2.3 空間復雜度
空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的量度 。空間復雜度衡量的是算法在執行過程中額外占用的存儲空間(不包括輸入數據本身占用的空間)。空間復雜度不是程序占用了多少bytes的空間,因為這個也沒太大意義,所以空間復雜度算的是變量的個數。空間復雜度計算規則基本跟時間復雜度類似,也使用大O漸進表示法。
舉個例子:
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}這個冒泡排序方法中僅使用了幾個固定的變量:end、sorted、i ,這些變量的占用的存儲空間不會隨著輸入數組的大小變化而變化,交換元素的 Swap方法也只需要臨時變量來交換兩個元素,同樣不依賴與數組規模。因此它的空間復雜度為3,使用大o的漸進表示法,得:O(1)。
3.泛型
3.1 包裝類
在Java中,由于基本數據類型不是繼承自Object,為了在泛型代碼中可以支持基本類型,Java給每個基本類型都對應了一個包裝類型。
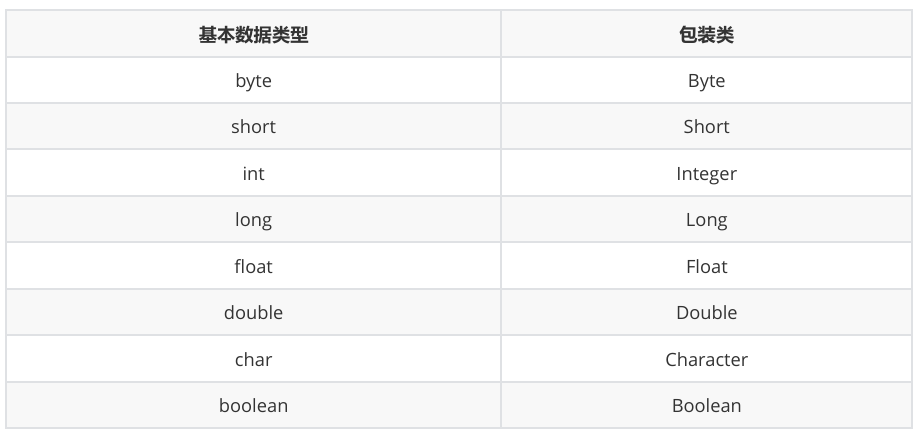
3.1.1 裝箱與拆箱
?裝箱(也叫裝包):把基本數據類型 變為 包裝類類型的過程叫做裝箱。
拆箱(也叫拆包):把保證類類型 變為 基本數據類型的過程叫做拆箱。
?int i = 10;
//裝箱操作,新建一個 Integer 類型對象,將 i 的值放入對象的某個屬性中
Integer i1 = Integer.valueOf(i);
Integer i2?= new Integer(i);
//拆箱操作,將 Integer 對象中的值取出,放到一個基本數據類型中
int j = i1.intValue();
3.1.2 自動裝箱與自動拆箱
?裝箱和拆箱分為自動和顯式,上述就是顯式裝箱和顯式拆箱。從顯示裝箱和顯式拆箱的使用過程來看,它們的操作帶來了不少的代碼量,所以為了減少開發者的負擔,Java提供了自動機制:
?int i = 10;
//自動裝箱
Integer i1 = i;
Integer i2?= (Integer)i;
//自動拆箱
int j = i1;
int k = (int)i1;
那么自動裝箱和自動拆箱的底層機制到底是怎么樣的呢?很簡單,底層是在我們使用自動裝箱和自動拆箱時,Java幫我們調用了具體的方法,也就是使用了顯式的方式。
?3.1.3 裝箱與拆箱的面試題
為什么下列的代碼的輸出結果不一樣?
public class Main {public static void main(String[] args) {Integer a = 100;Integer b = 100;System.out.println(a == b);Integer c = 200;Integer d = 200;System.out.println(c == d);}
}//運行結果
true
false
顯然這里涉及到了裝箱操作,我們都知道裝箱底層上是調用了 Integer.valueOf()方法,那么到Integer類中去找這個方法:
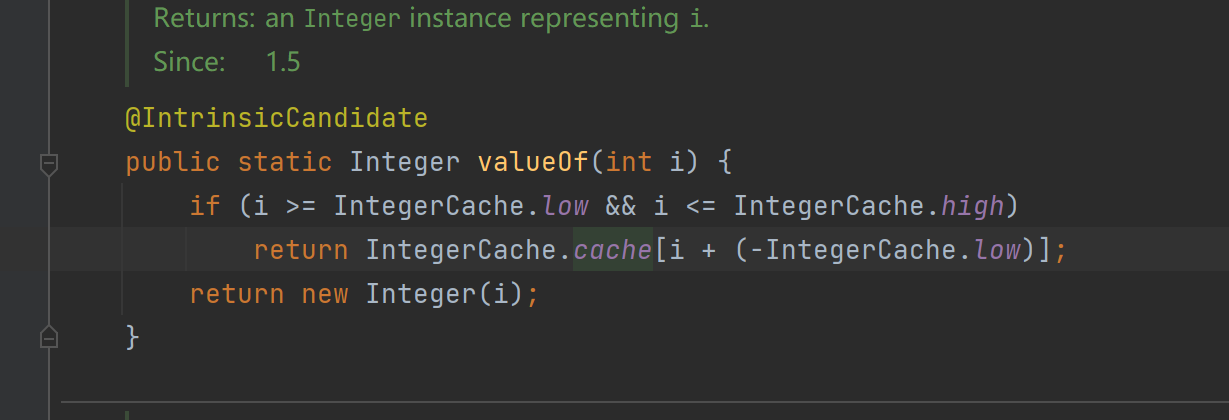
發現:當傳入的 i 在某個范圍內時,是從一個數組中直接去獲取值,當 i 在這個范圍內時,它返回一個新的 Integer對象。但是這個范圍是多少呢?繼續深挖,我們發現:
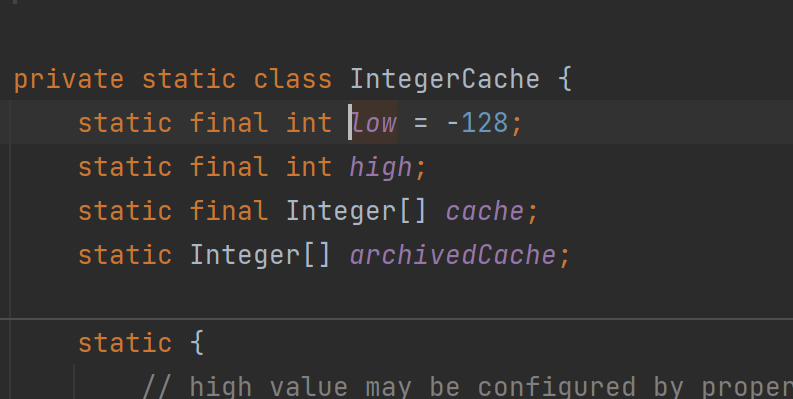
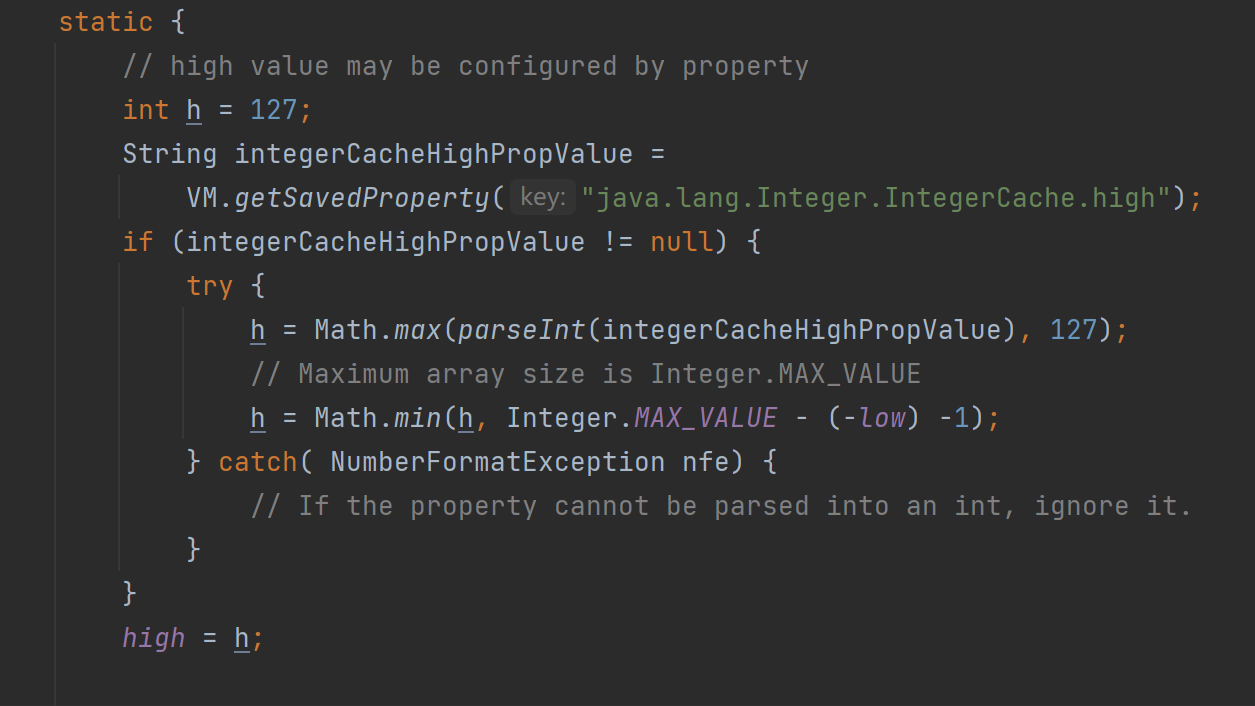
?low = -128,high = 127,因此得出結論:這個范圍是-128 到 127!這就解釋清楚了,因為傳入a和b的值為100,在這個范圍內,因此它們是從同一個數組內獲取的值,而傳入c和d的值為200,不在這個范圍內,因此它們的值分別來自新建的兩個Integer對象,用 == 進行比較,比較的是它們的地址,a和b來自同一個數組,因此地址相同,故輸出為true,而c和d是兩個不同的對象,因此地址不同,故輸出false。
?3.2 什么是泛型
一般的類和方法,只能使用具體的類型: 要么是基本類型,要么是自定義的類。如果要編寫可以應用于多種類型的代碼,這種刻板的限制對代碼的束縛就會很大,但泛型的出現打破了這種束縛。通俗講,泛型就是適用于許多類型。從代碼上講,就是對類型實現了參數化。
3.3 不使用泛型的問題
現在,要做一件事:實現一個類,類中包含一個數組成員,使得數組中可以存放如何類型的數據,也可以根據成員方法返回數組中某個下標的值。要解決這個問題,我們會想到:
- 以前學的數組,只能放指定類型的元素。
- 所有類的父類默認為Object類。
那么突發奇想——數組的類型能不能是Object類。
class MyArrays {public Object[] arrays = new Object[10];public void setArrays(int pop,Object obj) {this.arrays[pop] = obj;}public Object getArrays(int pop) {return this.arrays[pop];}
}public class Main {public static void main(String[] args) {MyArrays myArrays = new MyArrays();myArrays.setArrays(0,10);myArrays.setArrays(1,"10");//String str = myArrays.getArrays(2); //編譯報錯String str = (String) myArrays.getArrays(1);System.out.println(str);}
}
把代碼實現后我們發現:
- 任何的類型的數據都可以存放。
- 1號下標本身就是字符串,但是直接取出來會報錯,要強制類型轉換才不報錯。
雖然說,在這種情況下什么類型的數據都能放入數組中,但是我們還是希望它只能裝一種數據類型,而不是同時裝這么多類型。而泛型的主要目的就在這里了!就是指定當前的容器,只能裝什么類型的對象,讓編譯器去做檢測。?從而實現:想裝什么類型,就將什么類型作為參數傳入。
3.4 泛型的語法
//第一種語法格式
class 分析類名稱 <類型形參列表> {
? ? ? ? //這里可以使用類型參數
}
例如
class ClassName <T1,T2, .... ,Tn> {
}
//第二種語法格式
class 分析類名稱 <類型形參列表> extends 繼承的類 /* 這里可以使用類型參數*/?{
? ? ? ? //這里可以使用類型參數
}
例如
class ClassName <T1,T2, .... ,Tn> extends?ParentClass<T1> {
? ? ? ? //這里可以使用類型參數
}
借助泛型,原來的代碼我們可以改成這樣:
class MyArrays <T>{public Object[] arrays = new Object[10];public void setArrays(int pop,T obj) {this.arrays[pop] = obj;}public T getArrays(int pop) {return (T)this.arrays[pop];}
}
public class Main {public static void main(String[] args) {MyArrays<String> arrays= new MyArrays<>();arrays.setArrays(0,"1");arrays.setArrays(1,"hello");String str = arrays.getArrays(1);System.out.println(str);}
}//運行結果
hello完全符合我們的預期!
【注意】
- 類名之后的<T>代表占位符,表示當前類是一個泛型類
- 在main方法中,類型后面加入<String> 表示指定當前類型
- 用能夠接收數組元素的變量去接收數組元素不報錯,不需要強制類型轉換
- 當存放的元素與泛型類指定的元素不同時,會報錯,編譯器會在存放元素時幫助我們進行類型檢測
?3.5 泛型類的使用
使用的語法格式:
泛型類<類型參數> 變量名;? //定義一個泛型類引用
new 泛型類<類型參數>(構造方法實參);? //實例化一個泛型類對象
舉例
MyArray<Integer> list = new MyArrays<Integer>();
注意:泛型的類型實參只接受類,所有的基本數據類型必須使用包裝類!
類型推導
當編譯器可以可以根據上下文推導出類型實參時,可以省略類型實參的填寫,例如:
MyArray<Integer> list = new MyArrays< >();
?3.6 裸類型
裸類型是一個泛型類但沒有帶著類型實參,例如:
MyArray list = new MyArrays();
//這就是一個裸類型
?注意:我們不要自己去使用裸類型,因為裸類型是為了兼容老版本的 API 保留的機制。
3.7 泛型如何編譯
Java的泛型機制是在編譯時實現的(它的兩個功能:自動類型檢查和自動類型轉換),在編譯的過程中,編譯器會將所有的?T 替換為 T的上界類型,也就是說編譯結束后所有的 T 都被替換為了T的上界類型,這種機制稱為:擦除機制。
若沒有 T 沒有指定上界類型,那么默認指定Object類。
3.8 泛型的上界
在定義泛型類時,有時候需要對傳入的類型變量做一定的約束,可以通過類型邊界來約束。
具體的語法格式:
class 泛型類名稱<類型形參 extends 類型邊界>? {
? ? ? ? ……
}
舉例:
public class MyArrays<E extends Number> {
? ? ? ? ……
}
//意思是:只接受 Number 的子類型作為 E 的類型實參
注意:沒有指定類型邊界 E,可以視為 E extends Object
特殊場景
public class MyArrays<E extends Comparable<E>> {
? ? ? ? ……
}
//意思是:接收的 E 必須實現了Comparable接口,即extends后面加接口說明傳入的類型實參必須實現這個接口!
3.9 泛型方法
除了有泛型類,還有泛型方法,它的語法格式為:
方法限定符 <類型形參列表> 返回值類型 方法名稱(形參列表) {
? ? ? ? ……
}?
舉例:
class Alg {public <E> void Swap(E[] arrays,int i,int j) {E t = arrays[i];arrays[i] = arrays[j];arrays[j] = t;}
}?這是一個非靜態的泛型方法,當然也有靜態的泛型方法,即在public后面加 static即可。
關于泛型方法的使用一般有兩種:使用類型推導和不使用類型推導。這里拿非靜態的泛型方法舉例:
使用類型推導:
import java.util.Arrays;class Alg {public <E> void Swap(E[] arrays,int i,int j) {E t = arrays[i];arrays[i] = arrays[j];arrays[j] = t;}
}public class Main {public static void main(String[] args) {Integer[] arrays = {1,2,4,3};Alg alg = new Alg();alg.Swap(arrays,2,3);System.out.println(Arrays.toString(arrays));}
}//運行結果
[1, 2, 3, 4]不使用類型推導:
import java.util.Arrays;class Alg {public <E> void Swap(E[] arrays,int i,int j) {E t = arrays[i];arrays[i] = arrays[j];arrays[j] = t;}
}public class Main {public static void main(String[] args) {Integer[] arrays = {1,2,4,3};Alg alg = new Alg();alg.<Integer>Swap(arrays,2,3);System.out.println(Arrays.toString(arrays));}
}//運行結果
[1, 2, 3, 4]到此,數據結構的預備知識已經完結!感謝您的閱讀,如有錯誤還請指出!

)







)

)







