文本分類使用場景

• 文本分類任務
  
• 文本分類-機器學習
  

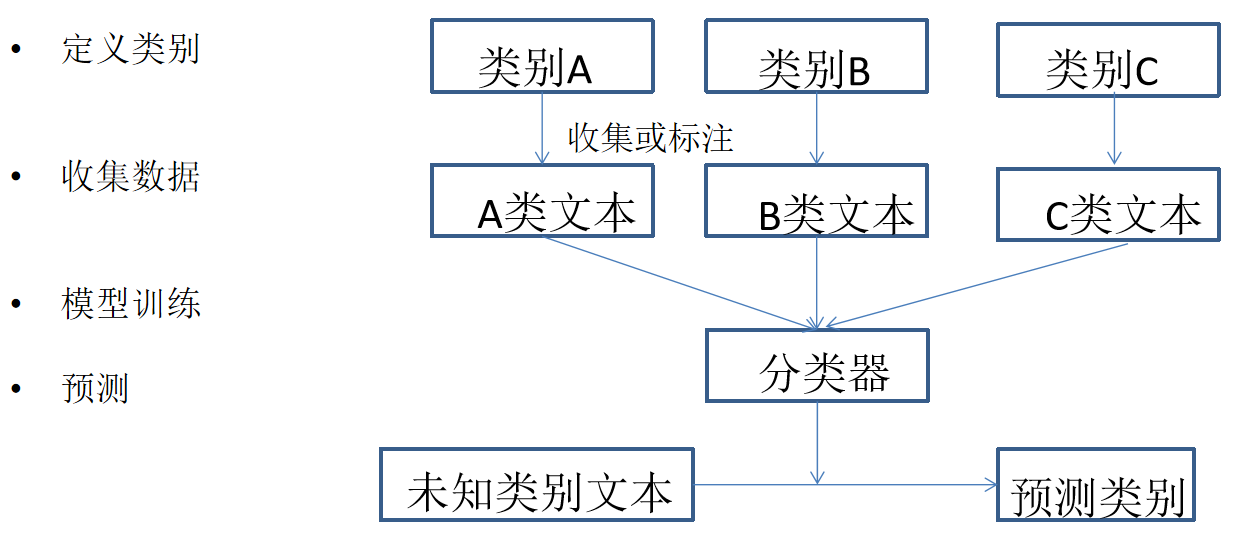
貝葉斯算法

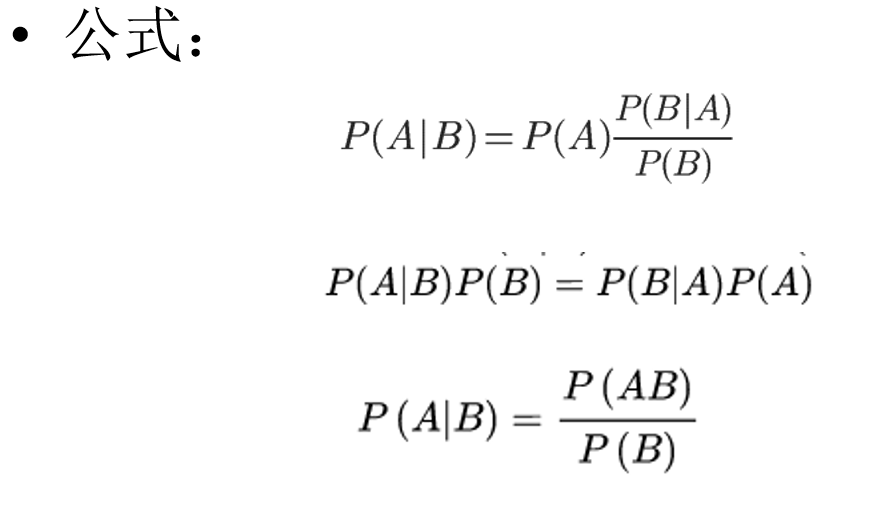
• 應用
  
  
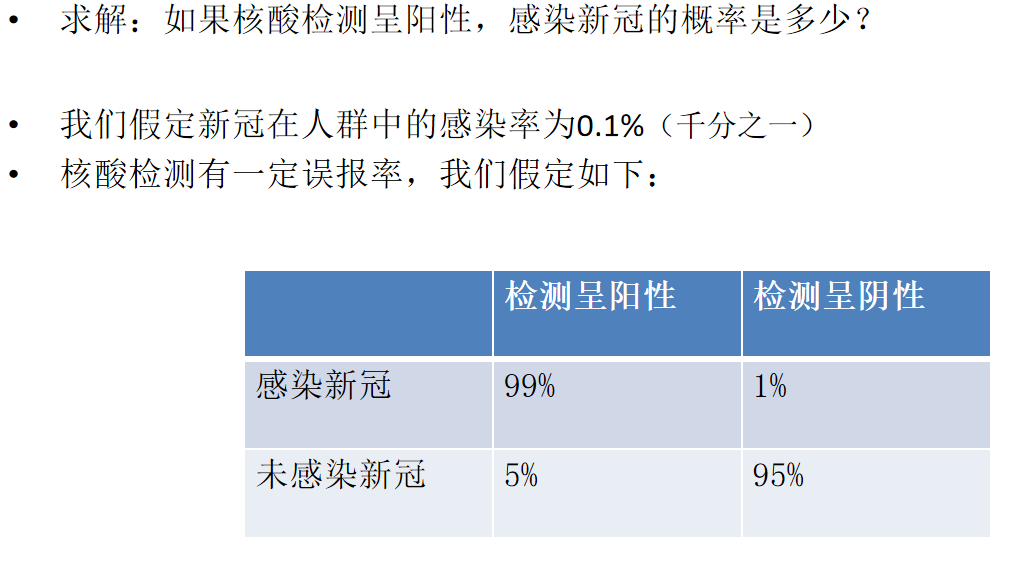
• 在NLP中的應用
  用貝葉斯公式處理文本分類任務
  一個合理假設：
  文本屬于哪個類別，與文本中包含哪些詞相關
  任務：
  知道文本中有哪些詞，預測文本屬于某類別的概率
  
• 貝葉斯算法優點
  1.簡單高效
  2.一定的可解釋性
  3.如果樣本覆蓋的好，效果是不錯的
  4.訓練數據可以很好的分批處理
• 貝葉斯算法缺點
  1.如果樣本不均衡會極大影響先驗概率
  2.對于未見過的特征或樣本，條件概率為零，失去預測的意義（可以引入平滑）
  3.特征獨立假設只是個假設
  4.沒有考慮語序，也沒有詞義
  

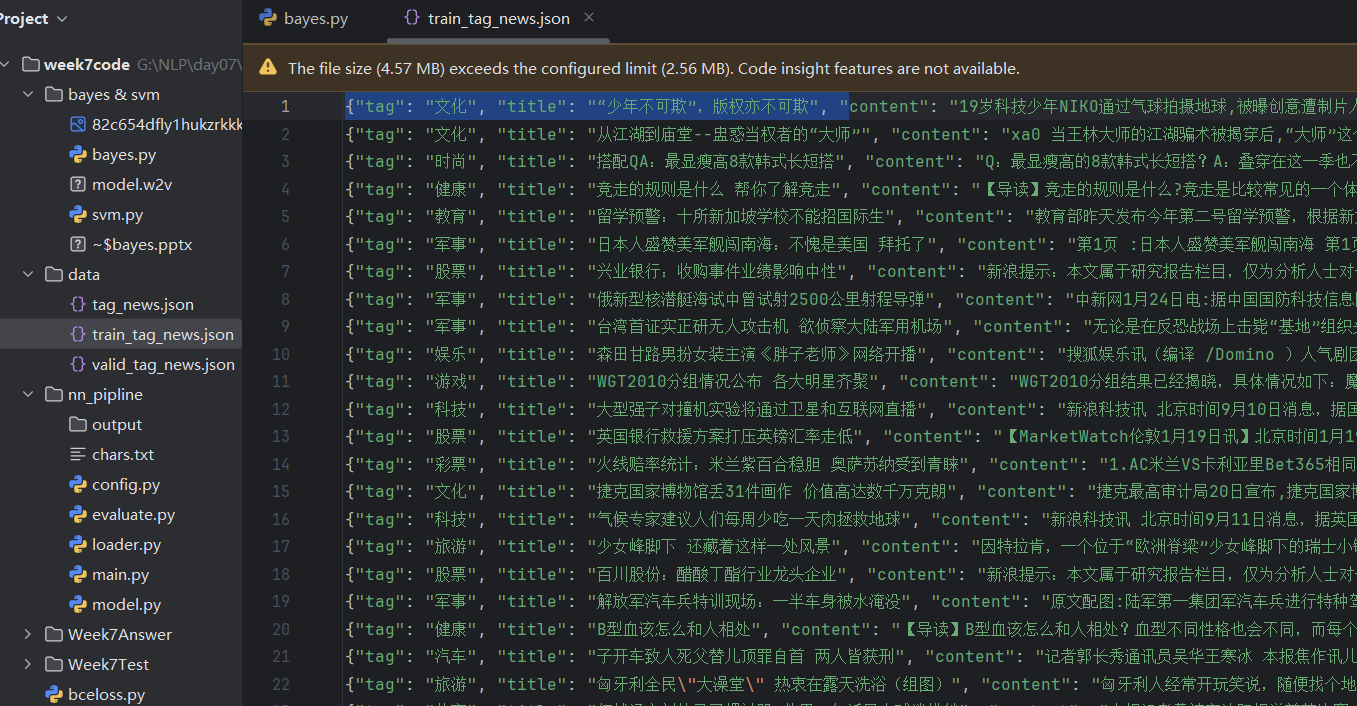
import jieba
import json
from collections import defaultdictjieba.initialize()
"""
貝葉斯分類實踐
P(A|B) = (P(A) * P(B|A)) / P(B)
事件A：文本屬于類別x1。文本屬于類別x的概率，記做P(x1)
事件B：文本為s (s=w1w2w3..wn)
P(x1|s) = 文本為s，屬于x1類的概率.   #求解目標#
P(x1|s) = P(x1|w1, w2, w3...wn) = P(w1, w2..wn|x1) * P(x1) / P(w1, w2, w3...wn)
P(x1) 任意樣本屬于x1的概率。x1樣本數/總樣本數
P(w1, w2..wn|x1) = P(w1|x1) * P(w2|x1)...P(wn|x1)  詞的獨立性假設
P(w1|x1) x1類樣本中，w1出現的頻率
公共分母的計算，使用全概率公式：
P(w1, w2, w3...wn) = P(w1,w2..Wn|x1)*P(x1) + P(w1,w2..Wn|x2)*P(x2) ... P(w1,w2..Wn|xn)*P(xn)
"""
class BayesApproach:def __init__(self, data_path):self.p_class = defaultdict(int)self.word_class_prob = defaultdict(dict)self.load(data_path)def load(self, path):self.class_name_to_word_freq = defaultdict(dict)self.all_words = set()  #匯總一個詞表with open(path, encoding="utf8") as f:for line in f:line = json.loads(line)class_name = line["tag"]title = line["title"]words = jieba.lcut(title)self.all_words = self.all_words.union(set(words))self.p_class[class_name] += 1  #記錄每個類別樣本數量word_freq = self.class_name_to_word_freq[class_name]#記錄每個類別下的詞頻for word in words:if word not in word_freq:word_freq[word] = 1else:word_freq[word] += 1self.freq_to_prob()return#將記錄的詞頻和樣本頻率都轉化為概率def freq_to_prob(self):#樣本概率計算total_sample_count = sum(self.p_class.values())self.p_class = dict([c, self.p_class[c] / total_sample_count] for c in self.p_class)#詞概率計算self.word_class_prob = defaultdict(dict)for class_name, word_freq in self.class_name_to_word_freq.items():total_word_count = sum(count for count in word_freq.values()) #每個類別總詞數for word in word_freq:#加1平滑，避免出現概率為0，計算P(wn|x1)prob = (word_freq[word] + 1) / (total_word_count + len(self.all_words))self.word_class_prob[class_name][word] = probself.word_class_prob[class_name]["<unk>"] = 1/(total_word_count + len(self.all_words))return#P(w1|x1) * P(w2|x1)...P(wn|x1)def get_words_class_prob(self, words, class_name):result = 1for word in words:unk_prob = self.word_class_prob[class_name]["<unk>"]result *= self.word_class_prob[class_name].get(word, unk_prob)return result#計算P(w1, w2..wn|x1) * P(x1)def get_class_prob(self, words, class_name):#P(x1)p_x = self.p_class[class_name]# P(w1, w2..wn|x1) = P(w1|x1) * P(w2|x1)...P(wn|x1)p_w_x = self.get_words_class_prob(words, class_name)return p_x * p_w_x#做文本分類def classify(self, sentence):words = jieba.lcut(sentence) #切詞results = []for class_name in self.p_class:prob = self.get_class_prob(words, class_name)  #計算class_name類概率results.append([class_name, prob])results = sorted(results, key=lambda x:x[1], reverse=True) #排序#計算公共分母：P(w1, w2, w3...wn) = P(w1,w2..Wn|x1)*P(x1) + P(w1,w2..Wn|x2)*P(x2) ... P(w1,w2..Wn|xn)*P(xn)#不做這一步也可以，對順序沒影響，只不過得到的不是0-1之間的概率值pw = sum([x[1] for x in results]) #P(w1, w2, w3...wn)results = [[c, prob/pw] for c, prob in results]#打印結果for class_name, prob in results:print("屬于類別[%s]的概率為%f" % (class_name, prob))return resultsif __name__ == "__main__":path = "../data/train_tag_news.json"ba = BayesApproach(path)query = "中國三款導彈可發射多彈頭 美無法防御很急躁"ba.classify(query)

支持向量機SVM

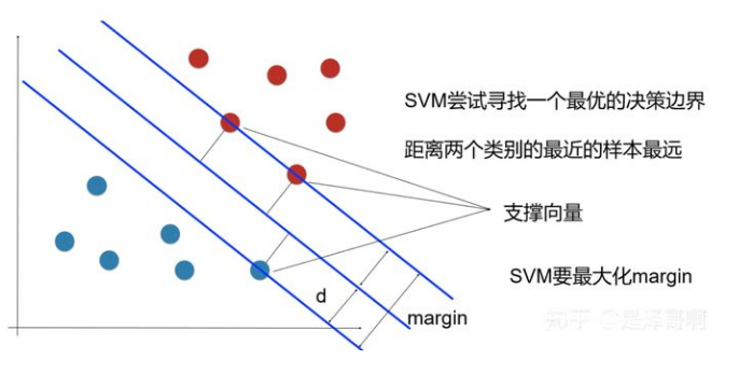
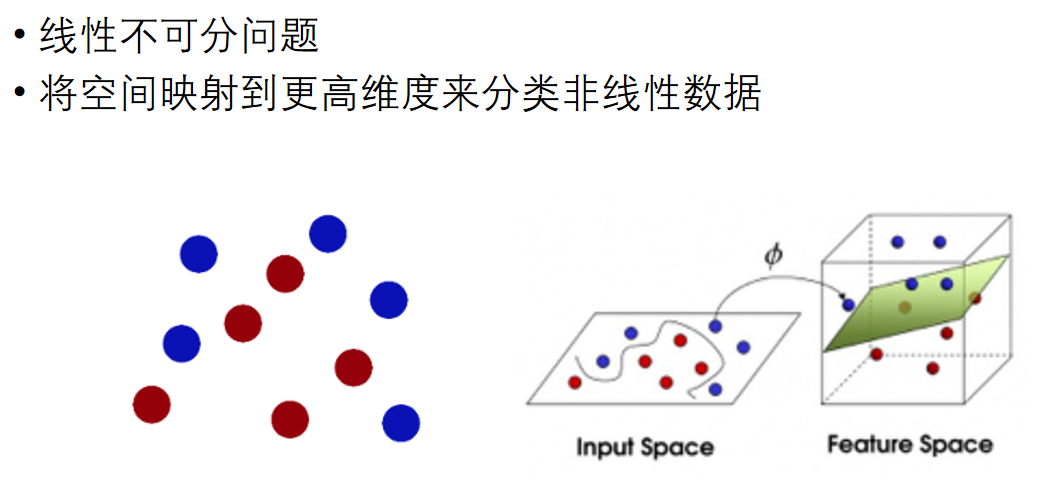
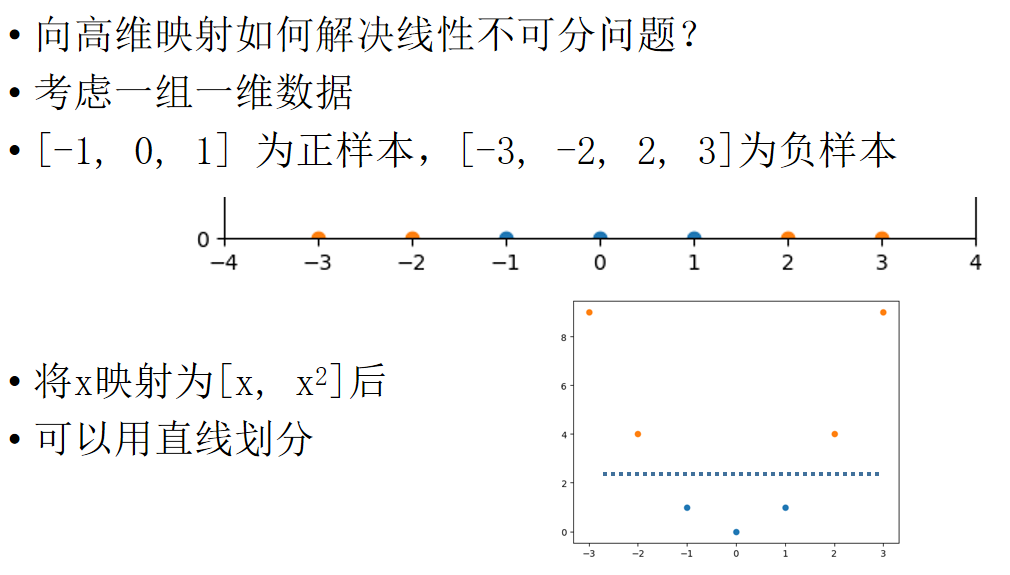
解決多分類

假設要解決一個K分類問題，即有K個目標類別

• one vs one方式
  建立 K(K - 1)/2 個svm分類器，每個分類器負責K個類別中的兩個類別，判斷輸入樣本屬于哪個類別
  對于一個待預測的樣本，使用所有分類器進行分類，最后保留被預測詞數最多的類別
  假設類別有[A,B,C]
  X->SVM(A,B)->A
  X->SVM(A,C)->A
  X->SVM(B,C)->B
  最終判斷 X->A

• one vs rest方式
  建立K個svm分類器，每個分類器負責劃分輸入樣本屬于K個類別中的“某一個類別，還是其他類別”
  最后保留預測分值最高的類別
  假設類別有[A,B,C]
  X->SVM(A,rest)->0.1
  X->SVM(B,rest)->0.2
  X->SVM(C,rest)->0.5
  最終判斷 X->C

• 支持向量機優點
  1.少數支持向量決定了最終結果，對異常值不敏感
  2.對于樣本數量需求較低
  3.可以處理高維度數據

• 支持向量機缺點
  1.少數支持向量決定了最終結果，對異常值不敏感
  2.對于樣本數量需求較低
  3.可以處理高維度數據

深度學習

---