前言:Prim算法是圖論中的算法,用來生成圖的最小生成樹。本篇文章介紹算法的流程,實現思想,和具體代碼實現,使用c語言。學習需要輸出才能理解的更透徹,所以說堅持寫文章,希望可以用自己的方式把一些知識的原理描述出來。我會結合示意圖清晰地展現出所有的流程,用人類語言把整個過程表述清楚,在寫代碼的時候才能做到胸有成竹,而不是模棱兩可或者說差不多就是這樣。本篇文章假設你已經具有了基本的數據結構和c語言的基礎。
分享一個學習算法的神奇網站,可以可視化算法的執行過程。
Prim算法
一、Prim算法實現思路
Prim算法的作用是實現圖的最小生成樹。
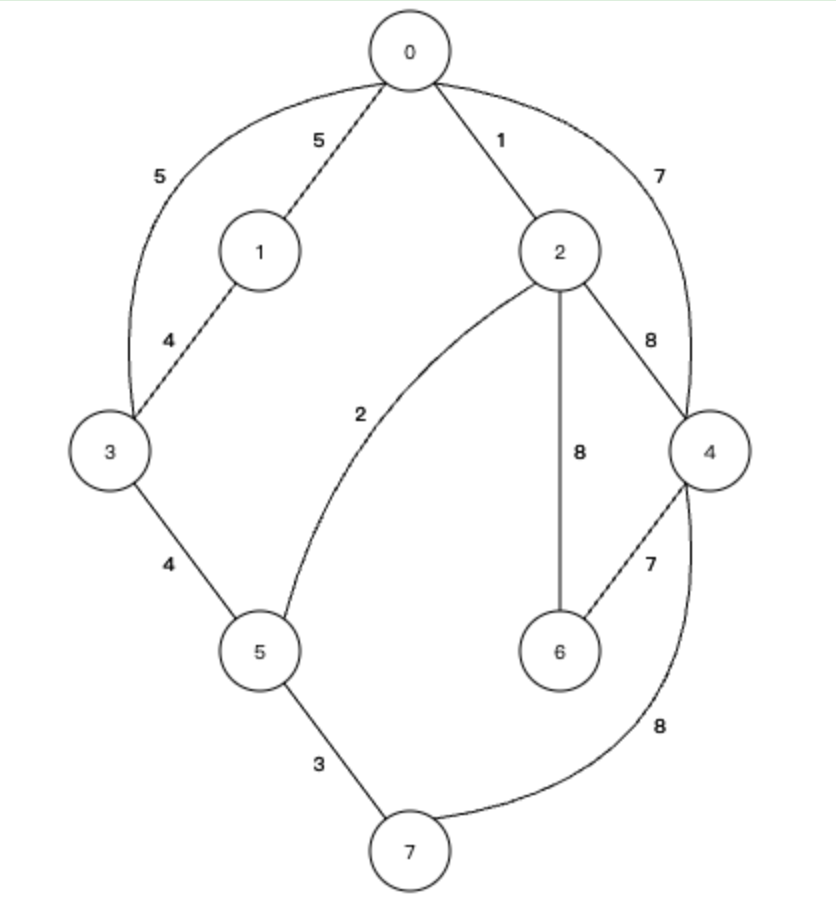
Prim算法使用的是貪心算法的策略,每次都會找和當前的節點相連的邊中,權值最小的節點。以上面這個圖為例,首先我們要確定最小生成樹的根節點,我們就設定為0節點。下面我們分步驟進行
① 根據貪心算法的原則,與0相連的下一個節點,我們要找0節點的邊中,權值最小的邊,0節點相連的一共有4條邊,分別是
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 2 | 1 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
找到權值最小的,就是連接2號節點的邊,權值為1,所以會將2號節點加入到最小生成樹中。
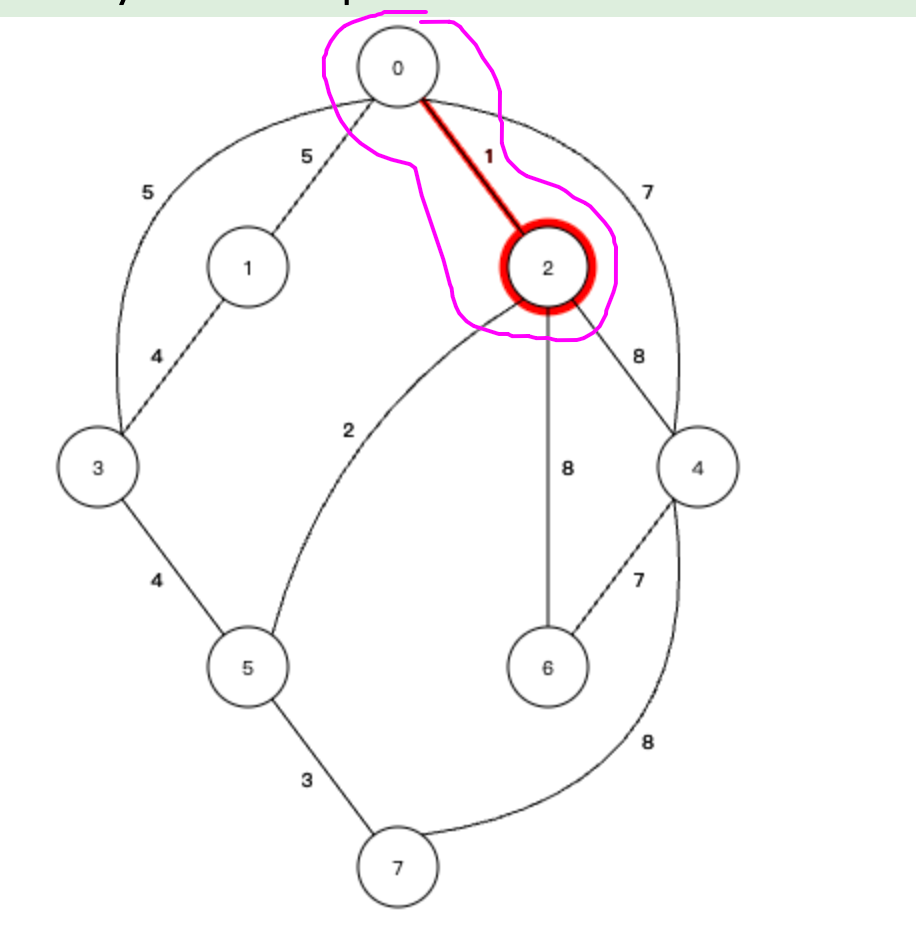
② 現在構成了圖中所畫的一棵生成樹,需要將這兩個節點看成一個整體,找和這棵生成樹相連的邊中,權值最小的邊,所有的邊:
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 5 | 2 |
| 2 | 6 | 8 |
最小的邊就是連接2號節點和五號節點的邊,權值為2,然后就將5號節點加入到生成樹中,并且5號節點連的是2號節點,就會生成下面這棵生成樹
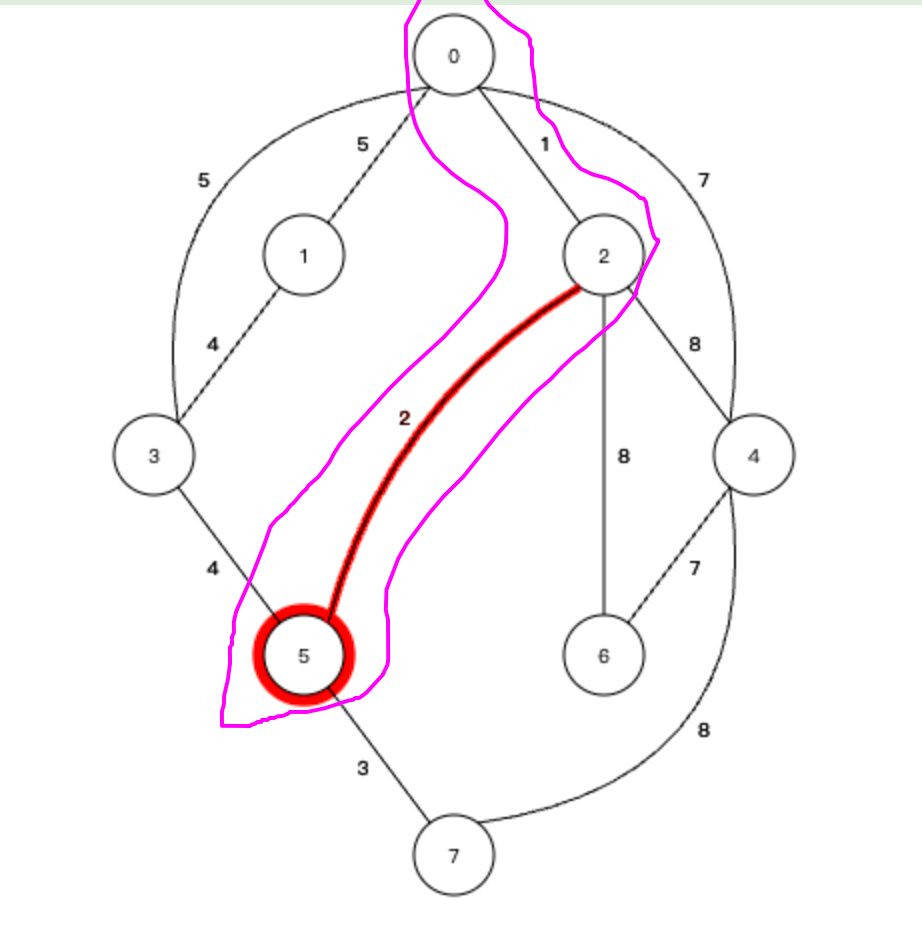
③接下來看和 1-2-5 生成樹相連的節點的權值,所有的邊:
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 5 | 7 | 3 |
| 5 | 3 | 4 |
權值最小的邊就是連接5號節點和3號節點的邊,權值為3,那么就將3號節點加入到生成樹中,生成樹如下:
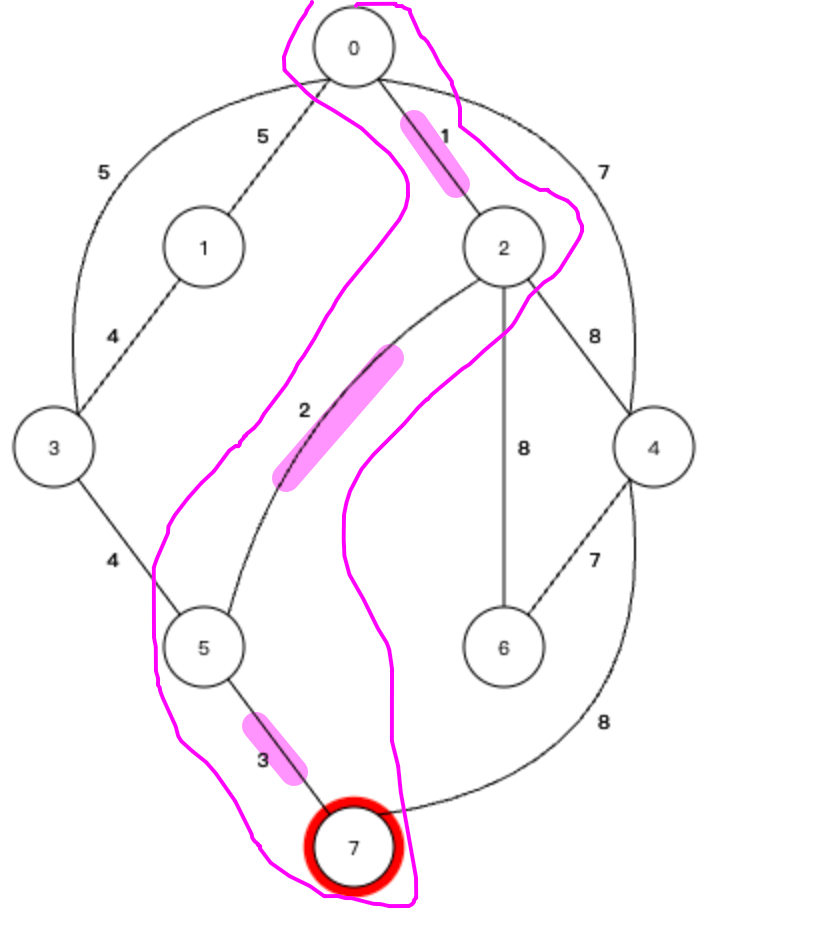
④ 再看和當前的生成樹相連的所有邊:
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 5 | 3 | 4 |
| 7 | 4 | 8 |
權值最小的邊是連接5號節點和3號節點的邊,權值為4,構成的生成樹如下:
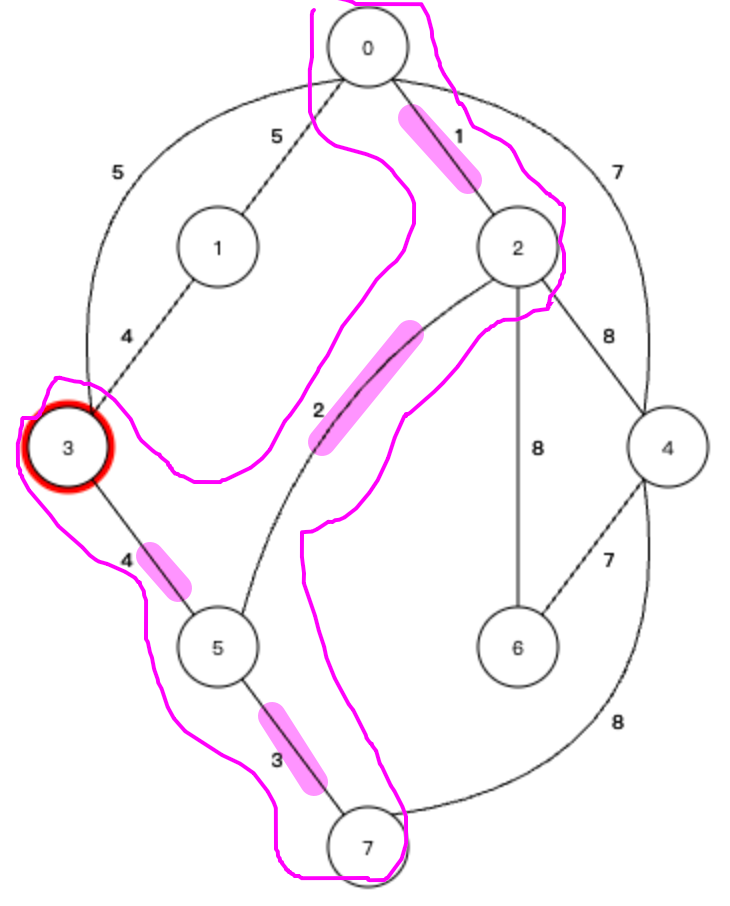
⑤ 這里有一個需要注意的地方,就是最小生成樹一定是不能有環,所以從3到0的邊就不能再考慮了,和當前生成樹相連的邊:
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 7 | 4 | 8 |
| 3 | 1 | 4 |
權值最小的邊是連接3號節點和1號節點的邊,權值為4,那么就將1號節點加入到生成樹:

⑥ 去除會形成回路的邊 0 -> 5, 和當前的生成樹相連的所有的邊:
| 起點 | 終點 | 權值 |
|---|---|---|
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 7 | 4 | 8 |
| 其中權值最小的邊是 連接0號節點和4號節點的邊,權值為7,將4號節點加入生成樹,形成下面一個生成樹: |
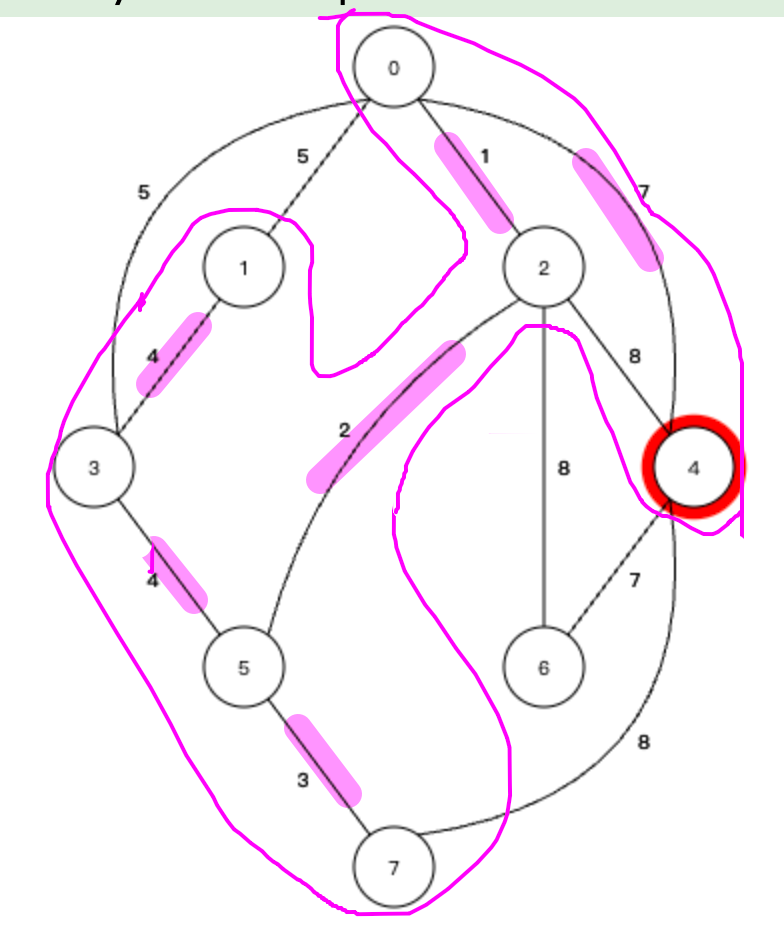
⑦ 此時的邊只有兩條了,因為形成回路的邊要去掉
| 起點 | 終點 | 權值 |
|---|---|---|
| 2 | 6 | 8 |
| 4 | 6 | 7 |
| 選擇連接4號節點和6號節點的邊,權值為7,至此所有的節點添加完畢 |
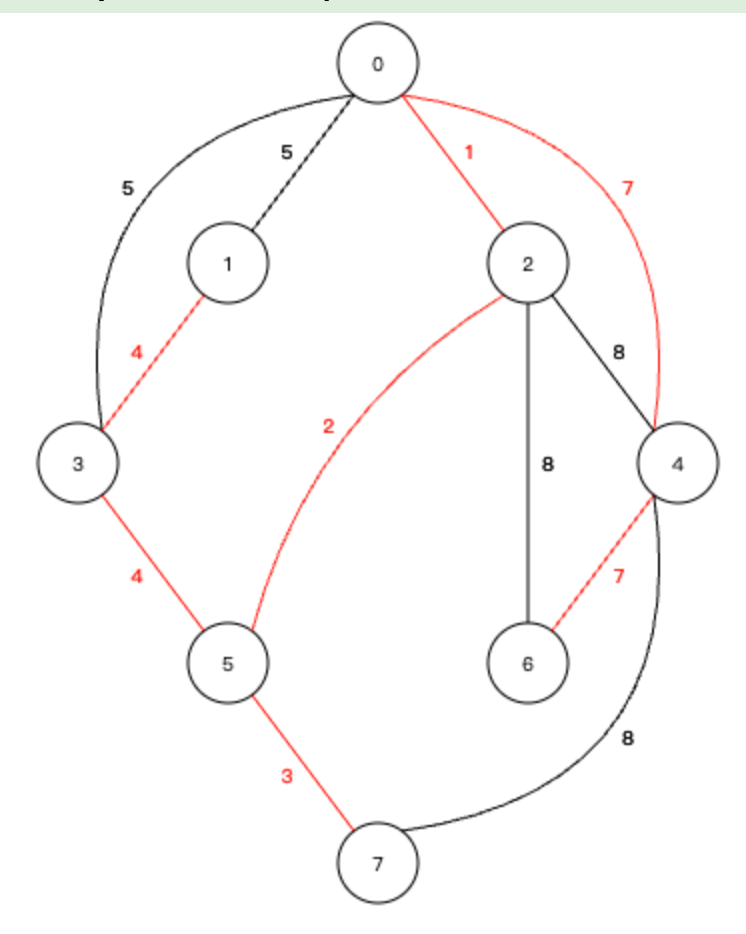
二、代碼實現
通過上面的文字描述和圖像展示,我們已經了解到了普利姆算法的執行的流程,接下來我們看一下代碼層面的實現。分析一個問題,首先是站在人類思維像上面一樣,寫出步驟,然后就是需要轉化成代碼。這個過程還是挺復雜的,比較抽象。
一個功能的代碼實現大概可以分為下面:
1、數據的類型、常量,需要定義結構體和常量,常量如最大值的限定等
2、入參
3、主函數
4、初始化輔助變量,需要分析都需要什么輔助的變量
5、流程執行
7、輸出結果,printf或者return
當然關鍵就是第五步,其實前置的步驟都是為第五步服務的。我們先分析一下主流程需要做什么:
1、找和當前生成樹相連的邊中權值最小的邊
2、將邊加入當前生成樹
3、需要記錄當前的節點相連的在生成樹中的節點,才能正確繪制樹
那么我們就需要一個數組,來存儲和當前生成樹直接相連的所有的邊的權值,其實就是節點到生成樹的距離,如果節點在生成樹內部,那么距離就是0,如果沒有直接相連,那么距離就是正無窮,這個數組的名字取做 lowcost,意為最低成本的構成樹,這個數組的初始化需要通過遍歷鄰接數組獲取,我們都假設樹的根節點為0號節點,那么lowcost 初始時就是0號節點到所有其他節點的距離,就是鄰接數組的第一行。
需要一個數組來記錄當前的節點相連的在生成樹中的節點,記為 adjvex 數組,意為臨近節點,初始化都為 0,
這兩個數組通過下標來和節點一一對應。
然后我們需要比較生成樹的邊中,權值最小的邊,也就是需要一個min變量,遍歷所有的邊,不斷更新min,讓它變成最小的權值,并且如果一個節點離生成樹的距離最小,我們還要記錄這個節點,記為 k。
k 節點需要加入到生成樹中,也就是將 k 節點放在生成樹中,也就是 k 節點對應的 lowcost[k] 要置為0,表示k節點到生成樹的距離為0,權值和距離其實是一個意思。
將 k 節點加入到生成樹中之后,還需要更新 adjvex 數組,想象一下,如果之前 0 -> 3 節點 沒有路徑,初始時 lowcost[3] = 正無窮,但是 0 -> 2 有路徑,并且 2 -> 3 有路徑,此時就需要更新 3 節點相連的節點,也就是 adjvex[3] 修改成 2,lowcost[3] = 2到3的距離,但是如果后面4號節點加入樹,并且 4-> 3 的路徑更短了,那就需要修改 adjvex[3] = 4,lowcost[3] = 4到3的距離。所以說需要對比從 k 到 j 的距離和當前的 lowcost[j],如果k 到 j 的距離更小,需要更新lowcost[j] = k到j的距離和adjvex[j] = k 。
上面流程走完之后,是實現了第一個權值最小的邊的節點加入到生成樹,所以整體需要循環n次,n為樹的節點數
接下來根據主流程分析一下需要初始化的數據:
1、需要兩層循環,i、j 作為循環變量
2、需要一個 min 值,初始化為一個c語言中的最大值
3、k 記錄權值最小的邊對應的節點
4、lowcost 數組,記錄權值
5、adjvex 數組,記錄鄰近節點
需要定義的數據結構和常量:
1、圖的結構體
2、MAXVEX 表示最大節點數
入參就是 圖
接下來看實際的代碼吧,相信通過上面的分析你已經非常清楚每句代碼的作用
// 普利姆算法
#include <stdio.h>
#include <limits.h>#define MAXVEX 100 // 最大頂點數// 圖的鄰接矩陣表示
typedef struct {int vexnum; // 頂點數int arcnum; // 邊數int arcs[MAXVEX][MAXVEX]; // 鄰接矩陣
} MGraph;void MiniSpanTree_Prim(MGraph G){int min,i,j,k;int adjvex[MAXVEX]; // 保存鄰接頂點下標的數組int lowcost[MAXVEX]; // 記錄當前生成樹到剩余頂點的最小權值lowcost[0] = 0; // 初始化第一個權值為0,即v0加入生成樹adjvex[0] = 0; // 將0號頂點作為第一個頂點加入到樹中for(i=1;i<G.vexnum;i++){ // 除了下標為0以外的所有頂點lowcost[i] = G.arcs[0][i]; // 將與下標為0的頂點有邊的權值存入lowcost數組adjvex[i] = 0; // 這些頂點的adjvex數組元素都為0}// 算法核心for(i=1;i<G.vexnum;i++){ // 只需要循環vexnum-1次min = INT_MAX; // 使用更合適的最大值j=0;k=0;// 找出lowcost中最小值,最小權值給min,最小值的下標給kfor(j=1;j<G.vexnum;j++){ // 從1號頂點開始找if(lowcost[j]!=0 && lowcost[j]<min){ // 不在生成樹中的頂點而且權值更小的min = lowcost[j]; // 更新更小的值k = j; // 找q到了新的點下標給k}}printf("邊(%d,%d) 權值:%d\n",adjvex[k],k,min); // 打印權值最小的邊lowcost[k] = 0; // 將這個頂點加入生成樹for(j=1;j<G.vexnum;j++){if(lowcost[j]!=0 && G.arcs[k][j]<lowcost[j]){ // 如果新加入的頂點k使權值更小lowcost[j] = G.arcs[k][j]; // 更新更小的權值adjvex[j] = k; //修改這條邊鄰接的頂點}}}
}// 初始化測試圖
void initTestGraph(MGraph *G) {int i, j;// 初始化鄰接矩陣為無窮大(用大數值表示)for(i = 0; i < MAXVEX; i++) {for(j = 0; j < MAXVEX; j++) {if(i == j) {G->arcs[i][j] = 0; // 自己到自己距離為0} else {G->arcs[i][j] = INT_MAX; // 無邊用最大值表示}}}// 設置頂點數G->vexnum = 6; // 0-5共6個頂點// 添加邊(無向圖,需要設置兩個方向)// 邊 0-1,權值4G->arcs[0][1] = G->arcs[1][0] = 4;// 邊 0-2,權值6 G->arcs[0][2] = G->arcs[2][0] = 6;// 邊 0-3,權值16G->arcs[0][3] = G->arcs[3][0] = 16;// 邊 1-2,權值10G->arcs[1][2] = G->arcs[2][1] = 10;// 邊 1-4,權值7G->arcs[1][4] = G->arcs[4][1] = 7;// 邊 2-3,權值14G->arcs[2][3] = G->arcs[3][2] = 14;// 邊 2-4,權值3G->arcs[2][4] = G->arcs[4][2] = 3;// 邊 2-5,權值8G->arcs[2][5] = G->arcs[5][2] = 8;// 邊 4-5,權值9G->arcs[4][5] = G->arcs[5][4] = 9;
}int main() {MGraph G;printf("=== 普里姆最小生成樹算法演示 ===\n\n");// 初始化測試圖initTestGraph(&G);printf("圖的頂點數:%d\n", G.vexnum);printf("圖的邊信息:\n");printf("0-1: 4, 0-2: 6, 0-3: 16\n");printf("1-2: 10, 1-4: 7\n");printf("2-3: 14, 2-4: 3, 2-5: 8\n");printf("4-5: 9\n\n");printf("開始執行普里姆算法:\n");printf("最小生成樹的邊:\n");// 執行普里姆算法MiniSpanTree_Prim(G);printf("\n================================\n");printf("算法執行完成!\n");printf("實際結果:總權值 = 4+6+3+8+14 = 35\n");return 0;
}




)








-day23)



)

)