二叉搜索樹（Binary Search Tree，簡稱 BST）是一種特殊的二叉樹，因其高效的查找、插入和刪除操作，成為計算機科學中最重要的數據結構之一。BST 的核心特性是 “左小右大”，這一特性使其在數據檢索、排序和索引等場景中發揮著關鍵作用。

---

二叉搜索樹的定義與核心性質

定義

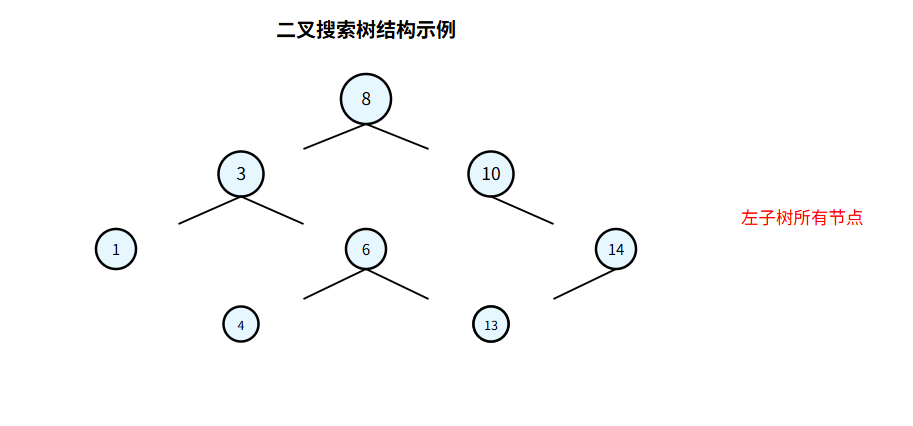
二叉搜索樹是一種二叉樹，其中每個節點的左子樹中所有節點的值小于該節點的值，右子樹中所有節點的值大于該節點的值。這一性質被稱為 “左小右大” 原則，且該原則對所有子樹都成立。

形式化定義：

對于 BST 中的任意節點node，滿足：

• 左子樹中所有節點的值 < node.val

• 右子樹中所有節點的值 > node.val

• 左子樹和右子樹本身也是二叉搜索樹

核心性質

1. 中序遍歷特性：BST 的中序遍歷（左→根→右）結果是嚴格升序的。這是 BST 最核心的性質，也是解決多數 BST 問題的關鍵。
2. 查找效率：在平衡的 BST 中，查找、插入、刪除操作的時間復雜度為O(logn)；在最壞情況下（如退化為鏈表），時間復雜度為O(n)。
3. 唯一性：給定一組數據，可能存在多個 BST 結構，但中序遍歷結果唯一（即數據的升序序列）。

結構圖示

二叉搜索樹的基本操作

查找操作

思路

利用BST“左小右大”的性質，從根節點開始：

- 若目標值等于當前節點值，返回該節點。

- 若目標值小于當前節點值，遞歸查找左子樹。

- 若目標值大于當前節點值，遞歸查找右子樹。

- 若遍歷到空節點，返回`null`（未找到）。

實現代碼

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}}public TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {return root;}return val < root.val ? searchBST(root.left, val) : searchBST(root.right, val);}

插入操作

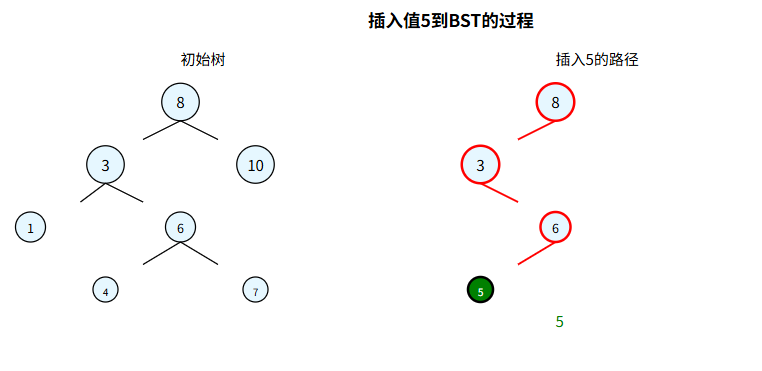
思路：插入過程類似查找，找到合適的空位置插入新節點：

• 若當前節點為空，創建新節點返回。

• 若插入值小于當前節點值，遞歸插入左子樹。

• 若插入值大于當前節點值，遞歸插入右子樹。

• （BST 通常不允許重復值，若需處理重復值，可約定插入右子樹）

插入過程圖示

實現代碼

public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null) {return new TreeNode(val); // 找到插入位置}if (val < root.val) {root.left = insertIntoBST(root.left, val); // 插入左子樹} else {root.right = insertIntoBST(root.right, val); // 插入右子樹}return root;}

刪除操作

刪除操作是 BST 中最復雜的操作，需根據節點的子樹情況分三種處理：

1. 葉子節點（無左右子樹）：直接刪除，返回null。
2. 單子樹節點（只有左或右子樹）：刪除節點，用子樹替代其位置。
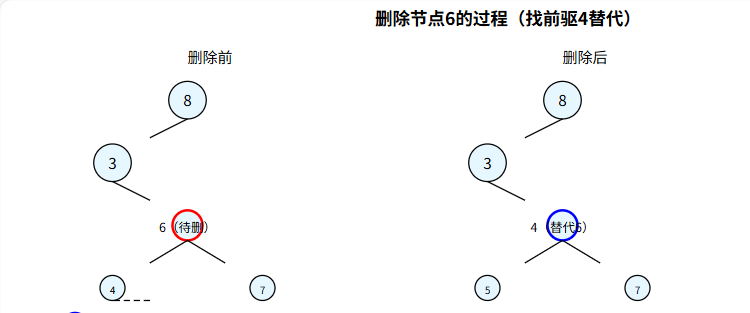
3. 雙子樹節點（有左右子樹）：

• • 找到該節點的前驅（左子樹中最大節點）或后繼（右子樹中最小節點）。

• • 用前驅（或后繼）的值替換當前節點的值。

• • 遞歸刪除前驅（或后繼）節點。

刪除過程圖示

（刪除節點 6）：

實現代碼：

public TreeNode deleteNode(TreeNode root, int key) {if (root == null) {return null; // 未找到待刪節點}if (key < root.val) {root.left = deleteNode(root.left, key); // 遞歸刪除左子樹} else if (key > root.val) {root.right = deleteNode(root.right, key); // 遞歸刪除右子樹} else {// 找到待刪節點，分三種情況if (root.left == null) {return root.right; // 無左子樹，用右子樹替代} else if (root.right == null) {return root.left; // 無右子樹，用左子樹替代} else {// 有左右子樹，找左子樹最大節點（前驅）TreeNode predecessor = findMax(root.left);root.val = predecessor.val; // 替換值root.left = deleteNode(root.left, predecessor.val); // 刪除前驅}}return root;}// 查找左子樹最大節點（最右節點）private TreeNode findMax(TreeNode node) {while (node.right != null) {node = node.right;}return node;}

LeetCode 例題實戰

例題 1：98. 驗證二叉搜索樹（中等）

題目描述：給你一個二叉樹的根節點 root ，判斷其是否是一個有效的二叉搜索樹。有效 BST 定義為：

• 節點的左子樹只包含小于當前節點的數。

• 節點的右子樹只包含大于當前節點的數。

• 所有左子樹和右子樹自身必須也是二叉搜索樹。

示例：

輸入：root = [2,1,3]

輸出：true（1<2<3，符合BST）

輸入：root = [5,1,4,null,null,3,6]

輸出：false（4的左子樹有3<4，但4<5不成立）

解題思路

利用 BST 中序遍歷為升序的特性，或遞歸檢查每個節點的左右邊界：

1. 中序遍歷法：中序遍歷 BST，若結果非嚴格升序，則不是有效 BST。
2. 遞歸邊界法：為每個節點設置上下邊界（low和high）：

• • 根節點的邊界為(-∞, +∞)。
• • 左子樹節點的邊界為(low, root.val)。

• • 右子樹節點的邊界為(root.val, high)。

• • 若節點值超出邊界，則無效。

方法 2（遞歸邊界法）Java 代碼

class Solution {public boolean isValidBST(TreeNode root) {return isValid(root, Long.MIN_VALUE, Long.MAX_VALUE);}private boolean isValid(TreeNode node, long low, long high) {if (node == null) {return true; // 空樹是有效BST}// 節點值必須在(low, high)范圍內if (node.val <= low || node.val >= high) {return false;}// 左子樹邊界：(low, node.val)，右子樹邊界：(node.val, high)return isValid(node.left, low, node.val) && isValid(node.right, node.val, high);}}

復雜度分析

• 時間復雜度：O (n)，遍歷所有節點一次。

• 空間復雜度：O (n)，遞歸棧深度最壞為 n（退化為鏈表）。

例題 2：108. 將有序數組轉換為二叉搜索樹（簡單）

題目描述：給你一個整數數組 nums ，其中元素已經按升序排列，請你將其轉換為一棵高度平衡的二叉搜索樹。高度平衡的二叉樹是指每個節點的左右兩個子樹的高度差的絕對值不超過 1。

示例：

輸入：nums = [-10,-3,0,5,9]

輸出：[0,-3,9,-10,null,5]（或其他平衡BST結構）

解題思路

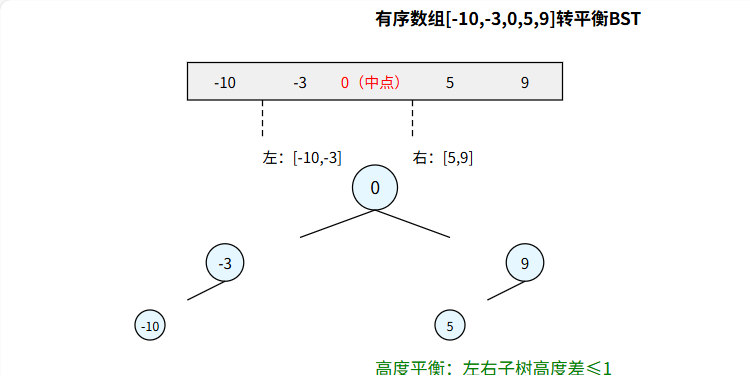
利用 BST 中序遍歷為升序的逆過程：

1. 選中間元素為根：平衡 BST 的根應是數組中間元素，確保左右子樹大小均衡。
2. 遞歸構建：

• • 左子樹由數組左半部分構建。
• • 右子樹由數組右半部分構建。

• • 遞歸終止條件：數組為空時返回null。

構建過程圖示

代碼實現

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return build(nums, 0, nums.length - 1);}private TreeNode build(int[] nums, int left, int right) {if (left > right) {return null; // 遞歸終止}// 選擇中間元素作為根（平衡關鍵）int mid = left + (right - left) / 2;TreeNode root = new TreeNode(nums[mid]);// 遞歸構建左右子樹root.left = build(nums, left, mid - 1);root.right = build(nums, mid + 1, right);return root;}}

復雜度分析

• 時間復雜度：O (n)，每個元素構建一個節點。

• 空間復雜度：O (logn)，遞歸棧深度為平衡樹的高度 logn。

考研 408 例題解析

例題 1：概念辨析題（選擇題）

題目：下列關于二叉搜索樹的敘述中，正確的是（ ）。

A. 二叉搜索樹的中序遍歷序列一定是遞增的

B. 二叉搜索樹中任意節點的左子樹高度一定小于右子樹高度

C. 對二叉搜索樹進行前序遍歷，再根據前序遍歷序列可以唯一重構該 BST

D. 在二叉搜索樹中查找某元素的時間復雜度一定是 O (logn)

答案：A

解析：

• A 正確：BST 的核心性質就是中序遍歷為嚴格遞增序列。

• B 錯誤：BST 不要求左右子樹高度平衡（平衡 BST 如 AVL 樹才要求）。

• C 錯誤：前序遍歷序列無法唯一重構 BST（如前序 [2,1,3] 和 [2,3,1] 可能對應不同 BST）。

• D 錯誤：在最壞情況下（退化為鏈表），查找時間復雜度為 O (n)。

例題 2：算法設計題（408 高頻考點）

題目：設計一個算法，在二叉搜索樹中找出第 k 小的元素，并分析算法的時間復雜度。

解題思路

利用 BST 中序遍歷為升序的特性，中序遍歷的第 k 個元素即為第 k 小元素：

1. 遞歸中序遍歷：記錄遍歷順序，當計數達到 k 時返回當前節點值。
2. 迭代中序遍歷：用棧模擬中序遍歷，彈出第 k 個節點時返回其值。

方法 2（迭代法）實現代碼

public int kthSmallest(TreeNode root, int k) {Deque<TreeNode> stack = new ArrayDeque<>();TreeNode curr = root;int count = 0;while (curr != null || !stack.isEmpty()) {// 左子樹入棧while (curr != null) {stack.push(curr);curr = curr.left;}// 彈出棧頂（中序遍歷的當前節點）curr = stack.pop();count++;if (count == k) {return curr.val; // 找到第k小元素}// 處理右子樹curr = curr.right;}return -1; // 無效輸入（k超出范圍）}

復雜度分析

• 時間復雜度：O (h + k)，h 為 BST 高度，最壞為 O (n + k)（鏈表），平均為 O (logn + k)。

• 空間復雜度：O (h)，棧存儲的節點數為樹的高度。

二叉搜索樹的擴展與應用

實際應用場景

• 數據庫索引：MySQL 的 B + 樹索引基于 BST 擴展，支持高效范圍查詢。

• 有序映射 / 集合：Java 中的TreeMap和TreeSet底層為紅黑樹（一種平衡 BST）。

• 排序與檢索：利用 BST 的插入和中序遍歷實現排序，時間復雜度 O (nlogn)。

與其他樹結構的關系

樹結構	特點	適用場景
二叉搜索樹（BST）	左小右大，中序升序	基礎檢索、排序
AVL 樹	平衡 BST，左右高差≤1	需嚴格平衡的場景
紅黑樹	近似平衡 BST，黑高一致	插入刪除頻繁的場景（如集合）
B + 樹	多路 BST，葉子節點成鏈表	數據庫索引

考研 408 備考要點

• 核心考點：BST 的定義與性質、中序遍歷特性、插入 / 刪除 / 查找操作。

• 重點掌握：

1. 利用中序遍歷解決 BST 相關問題（如驗證 BST、找第 k 小元素）。
2. 插入和刪除操作的遞歸實現，尤其是刪除時的節點替換邏輯。
3. BST 與平衡樹的區別，以及時間復雜度分析。

• 常見錯誤：
• • 忽略 BST 中 “嚴格大于 / 小于” 的約束（允許等于時需明確約定）。

• • 刪除節點時未正確處理雙子樹情況，導致 BST 性質被破壞。

總結

二叉搜索樹作為一種基礎且重要的數據結構，其 “左小右大” 的特性和中序遍歷升序的性質，使其在數據檢索和排序中有著廣泛應用。本文通過 LeetCode 例題（驗證 BST、有序數組轉 BST）展示了 BST 的核心應用，通過考研 408 例題解析了概念辨析和算法設計思路，結合 SVG 圖示直觀呈現了 BST 的結構及操作過程。

掌握 BST 的關鍵在于：

1. 深刻理解中序遍歷為升序這一核心性質，并用其解決各類衍生問題。
2. 熟練實現插入、刪除、查找等基本操作，尤其是刪除操作的三種情況處理。
3. 明確 BST 與平衡樹的區別，理解其時間復雜度的最壞與平均情況。

在考研備考中，BST 是數據結構部分的重點，需結合實例深入理解其操作原理和性質應用，為學習更復雜的樹結構（如紅黑樹、B + 樹）奠定基礎。

希望本文能夠幫助讀者更深入地理解二叉搜索樹算法，并在實際項目中發揮其優勢。謝謝閱讀！

---

希望這份博客能夠幫助到你。如果有其他需要修改或添加的地方，請隨時告訴我。