Mish

• 論文

  https://arxiv.org/pdf/1908.08681

函數+導函數

• Mish函數
  $$\begin{array}{rl}\text{Mish}(x)& =x?\tanh (\text{softplus}(x))\\ & =x?\tanh \left(\ln \right(1+e^x\left)\right)\end{array}$$

• Mish函數導數

  已知：
  $$
  \frac{d}{dx}\tanh(x) =1- \rm tanh ^2(x) \[2mm]

  \frac{d}{dx}\operatorname{Softplus}(x)=\sigma(x)=\frac{1}{1+e^{-x}}
  $$
  參考：

  神經網絡常見激活函數 2-tanh函數(雙曲正切)

  則：
  $$
  \begin{aligned}
  \frac{\mathrm{d}}{\mathrm{d}x}\text{Mish}(x)
  &= x \cdot \tanh!\Bigl(\ln!\bigl(1+e^{x}\bigr)\Bigr)\

  &=\frac{\mathrm{d}}{\mathrm{d}x}x\cdot\tanh\bigl(\ln(1+e^{x})\bigr) + x \cdot \frac{\mathrm{d}}{\mathrm{d}x}\tanh\bigl(\ln(1+e^{x})\bigr) \[2mm]

  &=\tanh\bigl(\ln(1+e^{x})\bigr) + x \cdot\bigl(1-\tanh^2(\ln(1+e{x})\bigr)\cdot\frac{1}{1+e^{-x}}\
  &=\tanh\bigl(\ln(1+e^{x})\bigr) + x \cdot\bigl(1-\tanh^2(\ln(1+e{x})\bigr)\cdot\sigma(x)
  \end{aligned}
  $$

---

函數和導函數圖像

• 畫圖

  import numpy as np
  from matplotlib import pyplot as pltdef mish(x):"""Mish(x) = x * tanh(softplus(x))"""sp = np.log(1 + np.exp(x))          # softplus(x)return x * np.tanh(sp)def mish_derivative(x):"""Mish'(x) = tanh(softplus(x)) + x * (1 - tanh2(softplus(x))) * sigmoid(x)"""sp = np.log(1 + np.exp(x))          # softplus(x)t  = np.tanh(sp)                    # tanh(softplus(x))s  = 1 / (1 + np.exp(-x))           # sigmoid(x)return t + x  * (1 - t ** 2) * sx = np.linspace(-4, 4, 1000)
  y = mish(x)
  y1 = mish_derivative(x)plt.figure(figsize=(12, 8))
  ax = plt.gca()
  plt.plot(x, y, label='Mish')
  plt.plot(x, y1, label='Derivative', linestyle='--')
  plt.title('Mish Activation Function and its Derivative')ax.spines['right'].set_color('none')
  ax.spines['top'].set_color('none')
  ax.xaxis.set_ticks_position('bottom')
  ax.spines['bottom'].set_position(('data', 0))
  ax.yaxis.set_ticks_position('left')
  ax.spines['left'].set_position(('data', 0))plt.legend(loc='upper left')
  plt.savefig('./mish.jpg',dpi=300)
  plt.show()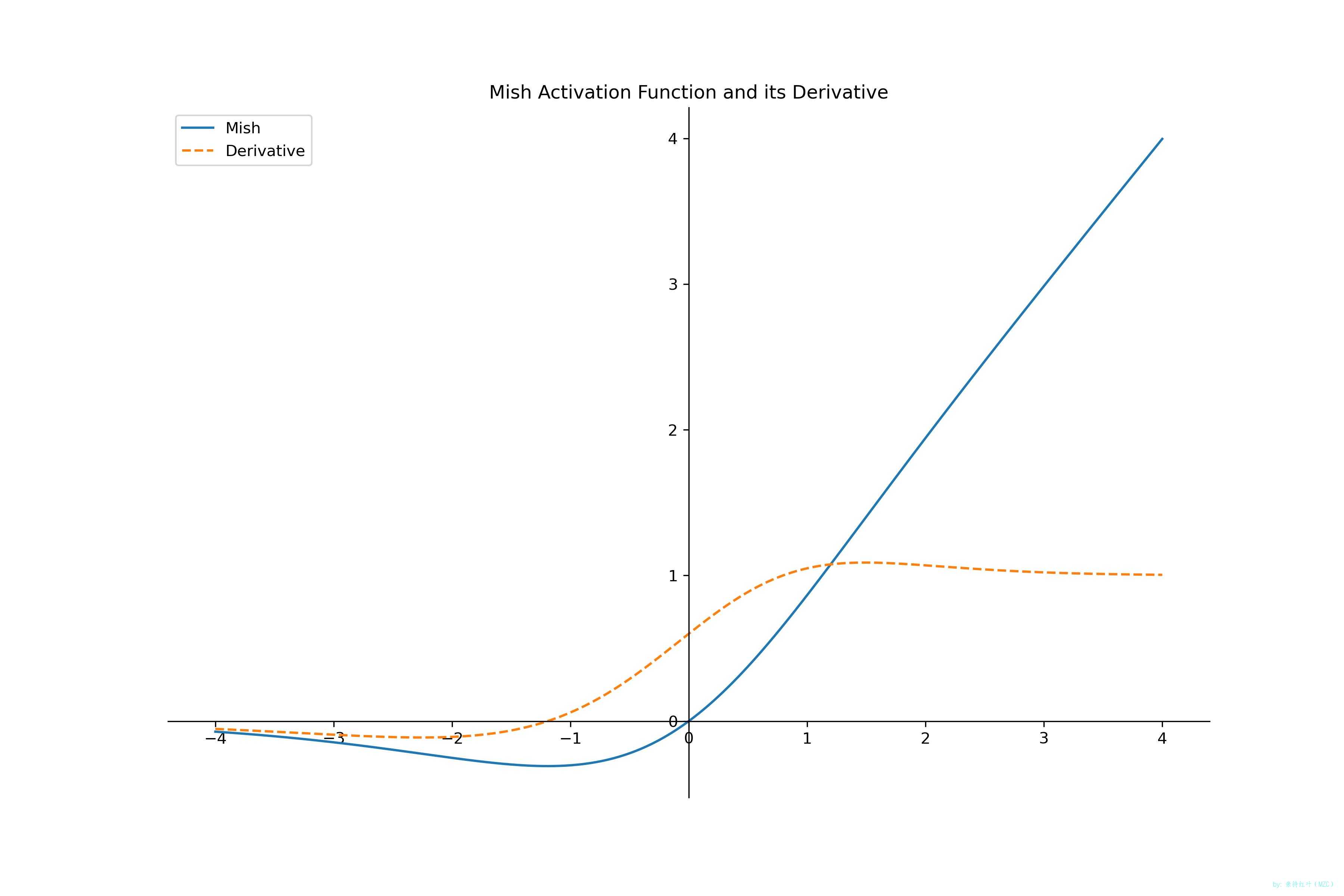
  

  

---

優缺點

• Mish 的優點

  1. 平滑無斷點：Mish 函數在整個實數域內連續可導，有助于穩定的梯度流，緩解梯度消失問題。
  2. 非單調性：負半軸有一段“下凹再回升”的曲線，有助于梯度流動，提升網絡的表達能力。
  3. 無上界正值：正值部分無飽和區，避免梯度消失，適合深層網絡，有有下界（≈ ?0.31）。
  4. 實驗性能：在 ImageNet、COCO 等多個基準上，Mish 常優于 ReLU、Swish 等激活函數。（并非絕對）

• Mish 的缺點

  1. 計算開銷大：相比 ReLU，需要額外計算 softplus、tanh 與乘法，推理延遲略高。
  2. 顯存占用：反向傳播需緩存中間結果，顯存開銷高于 ReLU。
  3. 并非萬能：在某些輕量級或實時任務中，性能提升可能無法抵消額外計算成本，需要實驗驗證。

---

PyTorch 中的 Mish 函數

• 代碼

  import torch
  import torch.nn.functional as F# 固定隨機種子
  torch.manual_seed(1024)      # CPU
  if torch.cuda.is_available():torch.cuda.manual_seed_all(42)   # GPU，如果有x = torch.randn(2,dtype=torch.float32)
  mish_x = mish(x)print(f"x:\n{x}")
  print(f"mish_x:\n{mish_x}")
  """輸出示例"""
  x:
  tensor([-1.4837,  0.2671])
  mish_x:
  [-0.29912564  0.18258688]
  

---

TensorFlow 中的 Mish 函數

• 環境

  python: 3.10.9
  tensorflow: 2.19.0

• 代碼

  import tensorflow as tfdef mish(x):return x * tf.math.tanh(tf.math.softplus(x))# 生成隨機張量
  x = tf.constant([-1.4837, 0.2671], dtype=tf.float32)
  mish_x = mish(x)print(f"x:\n{x.numpy()}")
  print(f"mish_x:\n{mish_x.numpy()}")"""輸出示例"""
  x:
  [-1.4837  0.2671]
  mish_x:
  [-0.29912373  0.18255362]
  

---