嵌入式學習-PyTorch（7）-day23

損失函數的調用

import torch
from torch import nn
from torch.nn import L1Lossinputs = torch.tensor([1.0,2.0,3.0])
target = torch.tensor([1.0,2.0,5.0])inputs = torch.reshape(inputs, (1, 1, 1, 3))
target = torch.reshape(target, (1, 1, 1, 3))
#損失函數
loss = L1Loss(reduction='sum')
#MSELoss均值方差
loss_mse = nn.MSELoss()
result1 = loss(inputs, target)
result2 = loss_mse(inputs, target)
print(result1, result2)

?實際應用

import torch
import torchvision.datasets
from torch import nn
from torch.nn import Conv2ddataset = torchvision.datasets.CIFAR10(root='./data_CIF', train=False, download=True, transform=torchvision.transforms.ToTensor())
dataloader = torch.utils.data.DataLoader(dataset, batch_size=1)class Tudui(nn.Module):def __init__(self):super().__init__()self.conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=5, padding=2)self.maxpool1 = nn.MaxPool2d(kernel_size=2)self.conv2 = nn.Conv2d(in_channels=32, out_channels=32, kernel_size=5, padding=2)self.maxpool2 = nn.MaxPool2d(kernel_size=2)self.conv3 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=5, padding=2)self.maxpool3 = nn.MaxPool2d(kernel_size=2)self.flatten = nn.Flatten()self.linear1 = nn.Linear(in_features=1024, out_features=64)self.linear2 = nn.Linear(in_features=64, out_features=10)self.model1 = nn.Sequential(Conv2d(in_channels=3, out_channels=32, kernel_size=5, padding=2),nn.MaxPool2d(kernel_size=2),nn.Conv2d(in_channels=32, out_channels=32, kernel_size=5, padding=2),nn.MaxPool2d(kernel_size=2),nn.Conv2d(in_channels=32, out_channels=64, kernel_size=5, padding=2),nn.MaxPool2d(kernel_size=2),nn.Flatten(),nn.Linear(in_features=1024, out_features=64),nn.Linear(in_features=64, out_features=10))def forward(self, x):x = self.model1(x)return x
loss = nn.CrossEntropyLoss()
tudui = Tudui()
for data in dataloader:imgs,targets = dataoutputs = tudui(imgs)result1 = loss(outputs, targets)print(result1)#反向傳播result1.backward()#梯度grad會改變，從而通過grad來降低loss

torch.nn.CrossEntropyLoss?

🧩 CrossEntropyLoss 是什么？

本質上是：

Softmax + NLLLoss（負對數似然） 的組合。

公式：

$\text{Loss} = - \sum_{i} y_i \log(\hat{p}_i)$

$\hat{p}_i$ ?：模型預測的概率（通過 softmax 得到）
$y_i$ ?：真實類別的 one-hot 標簽

PyTorch 不需要你手動做 softmax，它會直接從 logits（未經過 softmax 的原始輸出）算起，防止數值不穩定。

🏷? 常用參數

torch.nn.CrossEntropyLoss(weight=None, ignore_index=-100, reduction='mean')

參數	含義
`weight`	給不同類別加權（處理類別不均衡）
`ignore_index`	忽略某個類別（常見于 NLP 的 padding）
`reduction`	`mean`（默認平均）、`sum`（求和）、`none`（逐個樣本返回 loss）

🎨 最小使用例子

import torch
import torch.nn as nncriterion = nn.CrossEntropyLoss()# 假設 batch_size=3, num_classes=5
outputs = torch.tensor([[1.0, 2.0, 0.5, -1.0, 0.0],[0.1, -0.2, 2.3, 0.7, 1.8],[2.0, 0.1, 0.0, 1.0, 0.5]])  # logits
labels = torch.tensor([1, 2, 0])  # 真實類別索引loss = criterion(outputs, labels)
print(loss.item())

outputs：模型輸出 logits，不需要 softmax；
labels：真實類別（索引型），如 0, 1, 2,...；
loss.item()：輸出標量值。

💡 你需要注意：

?? 重點	📌 說明
logits 直接輸入	不要提前做 softmax
label 是類別索引	不是 one-hot，而是整數（如 `[1, 3, 0]`）
自動求 batch 平均	默認 `reduction='mean'`
多分類用它最合適	二分類也能用，但 `BCEWithLogitsLoss` 更常見

🎁 總結

優點	缺點
? 簡單強大，適合分類	? 不適合回歸任務
? 內置 softmax + log	? label 不能是 one-hot
? 數值穩定性強	? 類別極度不均衡需額外加 `weight`

🎯 一句話總結

CrossEntropyLoss 是深度學習中分類問題的“首選痛點衡量尺”，幫你用“正確標簽”去教訓“錯誤預測”，模型越聰明 loss 越小。

?公式：

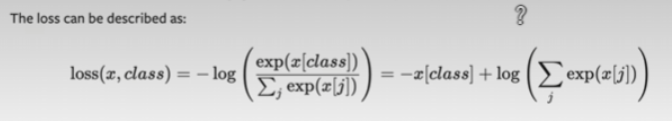
1?? 第一部分：

$- \log \left( \frac{\exp(x[\text{class}])}{\sum_j \exp(x[j])} \right)$

這是經典 負對數似然（Negative Log-Likelihood）：

分子：你模型對正確類別 class 輸出的得分（logits），取 exp；
分母：所有類別的 logits 做 softmax 歸一化；
再取負 log —— 意思是“你對正確答案預測得越自信，loss 越小”。

2?? 推導為：

$= - x[\text{class}] + \log \left( \sum_j \exp(x[j]) \right)$

log(a/b) = log(a) - log(b) 的變形：

$- x[\text{class}]$ ：你對正確類輸出的分值直接扣掉；
$+\log(\sum_j \exp(x[j]))$ ：對所有類別的總分值做歸一化。

這是交叉熵公式最常用的“log-sum-exp”形式。

📌 為什么這么寫？

避免直接用 softmax（softmax+log 合并后可以避免數值不穩定 🚀）
計算量更高效（框架底層可以優化）

🌟 直觀理解：

場景	解釋
正確類分數高	$x[\text{class}]$ 越大，loss 越小
錯誤類分數高	$\sum \exp(x[j])$ 越大，loss 越大
目標	壓低 log-sum-exp，拉高正確類別 logits

🎯 一句話總結：

交叉熵 = “扣掉正確答案得分” + “對所有類別歸一化”，越接近正確答案，loss 越小。
這就是你訓練神經網絡時 模型越來越聰明的數學依據 😎

舉例：

logits = torch.tensor([1.0, 2.0, 0.1])  # 模型輸出 (C=3)
label = torch.tensor([1])  # 真實類別索引 = 1

其中：

N=1（batch size）
C=3（類別數）
正確類別是索引1，對應第二個值：2.0

🎁 完整公式回顧

$\text{loss}(x, y) = -x[y] + \log \sum_{j} \exp(x[j])$

🟣 第一步：Softmax + log 邏輯

softmax 本質上是：

$p = \frac{\exp(x[\text{class}])}{\sum_j \exp(x[j])}$

但是 PyTorch 的 CrossEntropyLoss 內部直接用：

$\text{loss} = - \log p$

🧮 你這個例子手動算：

logits = [1.0, 2.0, 0.1]，class = 1，對應 logit = 2.0

第一部分：

$- x[\text{class}] = -2.0$

第二部分：

$\log \sum_{j=1}^{3} \exp(x[j]) = \log (\exp(1.0) + \exp(2.0) + \exp(0.1))$

先算：

exp(1.0)≈2.718
exp(2.0)≈7.389
exp(0.1)≈1.105

加起來：

∑=2.718+7.389+1.105=11.212

取對數：

log?(11.212)≈2.418

最終 loss：

loss=?2.0+2.418=0.418

🌟 你可以這樣理解：

部分	含義
?x[class]- x[\text{class}]?x[class]	懲罰正確答案打分太低
log?∑exp?(x)\log \sum \exp(x)log∑exp(x)	考慮所有類別的對比，如果錯誤類別打分高也被懲罰
最終目標	“提升正確答案打分、降低錯誤答案打分”

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/914873.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/914873.shtml
英文地址，請注明出處：http://en.pswp.cn/news/914873.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！