在機器學習的世界里，模型們就像一群努力破案的偵探，而數據就是它們的“犯罪現場”。今天，咱們的主角——一個自命不凡的分類模型，接到了一個看似簡單的任務：揪出那些患有罕見疾病的患者。這聽起來是不是很容易？畢竟，只要隨便猜猜，就能蒙對大部分結果，輕松拿下高得嚇人的準確率。

可別急，事情沒那么簡單！這個任務背后藏著一個巨大的陷阱，那就是數據的“偏見”——患病的人太少啦！這就像是在一個全是好人的人群里找壞蛋，要是隨便抓幾個好人當嫌疑人，那可就太冤枉人家了。我們的模型偵探們必須使出渾身解數，用各種聰明的指標來衡量自己的表現，才能真正找到那些隱藏在人群中的“壞蛋”。

接下來，就讓我們一起看看，這些模型偵探們是怎么一步步解開這個謎團的吧！

用性能指標評估分類模型

親愛的機器學習小伙伴們，快來看看這個有趣的情景吧：

假設你被安排去構建一個機器學習模型，用來檢測醫學患者是否感染了一種罕見疾病。這種疾病實在是太罕見了，患者感染的概率只有1%。你的上司希望你構建的模型能達到最高的準確率。這將是一個二分類器，以患者的信息作為輸入，然后告訴你患者是否患有該疾病，我們可以將輸出分別編碼為1（患病）或0（未患病）。

接下來的幾天，你充分發揮自己的機器學習技能，構建了一個準確率達到85%的模型。干得漂亮！

然而，你的快樂并沒有持續太久，因為你的上司告訴你，團隊里的另一個成員只花了大約10分鐘就構建了一個更簡單的模型，輕松實現了99%的準確率。

啥？！這是咋回事呢？難道那個團隊成員是個超級天才，還是公司給的指令有問題，或者我不是自己想象中的那么厲害的機器學習從業者？

讓我們來一探究竟吧！

性能指標

在機器學習的任何領域，我們都應該從最基本的定義和原理出發。

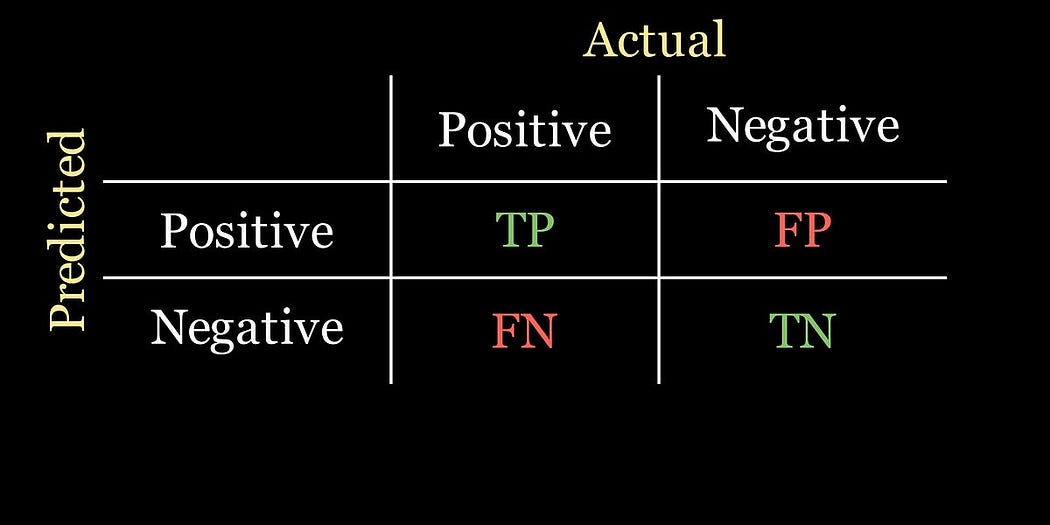
我們先從混淆矩陣說起，它展示了我們的模型預測得好不好。對于我們的二分類問題，它看起來像一個2×2的網格：第一列給出了實際患有疾病患者的數量，第二列給出了實際未患病患者的數量；行則對應模型做出的預測。舉個例子：

從現在開始，我們將疾病檢測稱為“陽性”結果，沒有檢測到疾病為“陰性”結果。也就是說，當模型認為檢測到疾病實例時，就會發出陽性信號。

混淆矩陣中的每個單元格代表一定的數量：

• 真陽性（TP）：模型預測患者患有疾病，且患者實際確實患有疾病的人數。
• 假陽性（FP）：模型預測患者患有疾病，但患者實際并沒有患病的人數。
• 假陰性（FN）：模型預測患者沒有患病，但患者實際患有疾病的人數。
• 真陰性（TN）：模型預測患者沒有患病，且患者實際確實沒有患病的人數。

以下是混淆矩陣的示意圖：

回想一下，公司讓你構建一個優化準確率的模型。分類器的準確率是正確分類點的比例：

$$\text{準確率}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{FN}+\text{TN}}$$

由于這是一個比例，準確率的值將在0到1之間，我們也可以將其轉換為百分比。

醫學奇跡

讓我們暫停一下，思考一下公司給我們的分類任務。我們知道，我們數據中只有1%的患者實際上患有這種疾病。因此，如果我們的數據集中有1000名患者，那么只有10人真正患有這種疾病。對于這個問題，分類器的最佳混淆矩陣場景如下：

事實上，對于任何混淆矩陣，最優分類器是其混淆矩陣僅在主對角線上有值的那個。

按照上面給出的公式，這個分類器的準確率是

$$\text{準確率}=\frac{10+990}{10+0+0+990}=1$$

🤔 你能看出我們如何構建一個準確率達到99%的超簡單分類器嗎？

💡 我們只需預測每個患者都沒有患病即可。這被稱為天真分類器，其混淆矩陣如下：

對應的準確率現在是

$$\text{準確率}=\frac{0+990}{0+0+10+990}=0.99$$

瞧！毫不費力就實現了99%的準確率。現在我們知道同事是怎么輕松實現這么高準確率的了……

但更重要的問題是，我們同事的分類器是不是一個好的分類器呢？盡管準確率很高，但它的設計并沒有真正檢測出任何疾病的實例！它只是默認說任何數據實例都沒有疾病。

主要問題是：準確率指標并不適合像我們正在討論的這種存在嚴重類別不平衡的數據集。

所以，使用準確率作為模型的性能指標并不總是明智的。那我們該怎么辦呢？

召回率

鑒于疾病診斷的背景，我們希望一個優先檢測疾病的分類器。我們可以使用的一個指標是召回率：

$$\text{召回率}=\frac{\text{TP}}{\text{TP}+\text{FN}}$$

分類器的召回率告訴我們，被模型分類為患有疾病的實際患有疾病的患者比例。

另一種說法是：在所有模型預測患有疾病的患者中，實際患有疾病的百分比是多少？

對于醫療診斷來說，這個指標比準確率更適合，因為我們不希望模型遺漏任何疾病的實例。我們不太關心模型輸出了多少假陽性（即模型預測患者患病，但實際上患者并沒有患病）。相反，我們需要盡可能降低假陰性值，否則就會有患有罕見疾病的患者卻不知道自己患病。

盡管假陽性很不方便，但假陰性是有害的。

讓我們看看天真分類器的召回率是什么樣的：

$$\text{召回率}=\frac{0}{0+10}=0$$

哦，這下就對了。

精確率

召回率性能指標適用于我們不想出現太多假陰性的情況。但如果在某些情境下，標記假陽性太不方便而不能忽視呢？

精確率是另一個性能指標，它衡量實際為正的正分類的比例：

$$\text{精確率}=\frac{\text{TP}}{\text{TP}+\text{FP}}$$

當希望向模型強調不要不必要地標記假陽性時，這個指標很有用。例如，在電子郵件垃圾郵件檢測的情境中，過多的假陽性可能意味著重要郵件最終會出現在你的垃圾郵件文件夾中！這當然不太理想。

F1 分數

你的問題背景可能需要結合精確率和召回率的一些特點。F1 分數在精確率和召回率之間提供了平衡：

$$\text{F1?分數}=2\times \frac{\text{精確率}\times \text{召回率}}{\text{精確率}+\text{召回率}}$$

也就是說，F1 分數是精確率和召回率的調和平均值。我們也可以用 TP、FP 和 FN 來表示 F1 分數公式：

$$\text{F1?分數}=\frac{2\times \text{TP}}{2\times \text{TP}+\text{FP}+\text{FN}}$$

我們可以看到，當 FP 和 FN 的算術平均值較高時，F1 分數會受到影響。特別是，僅最小化 FP 或 FN 中的一個是不夠的。

總的來說，F1 分數是在處理不平衡數據集時的一個有用指標。

小小的注意事項

似乎對于混淆矩陣中預測值和實際值應該如何顯示，并沒有全球統一的共識。在本文中，我將預測值放在行上，實際值放在列上。總之，當查看在線資源時要小心，因為有些可能使用的是我所描述的轉置版本。

總結一下

性能指標對于評估模型性能至關重要，有助于以符合預測目標的方式進行評估。希望這篇文章能幫你理解模型評估時需要考慮的細微差別。現在，像往常一樣，簡單總結一下：

• 準確率：告訴你模型正確分類的數據點比例。這個指標并不適合包含類別不平衡的數據集。
• 召回率：表示實際為正的數據點中被預測為正的比例。當你希望盡量減少模型漏掉的陽性結果時，這個指標很理想。召回率關注混淆矩陣的第一列。
• 精確率：表示被預測為正的數據點中實際為正的比例。當你希望盡量減少模型做出的錯誤陽性預測時，這個指標很理想。精確率關注混淆矩陣的第一行。

下面的動畫中，綠色和紅色的高亮顯示幫助我記住召回率和精確率在混淆矩陣中的位置：