1.? P1760 通天之漢諾塔 題解

題目背景

直達通天路·小A歷險記第四篇

題目描述

在你的幫助下，小 A 成功收集到了寶貴的數據，他終于來到了傳說中連接通天路的通天山。但是這距離通天路仍然有一段距離，但是小 A 突然發現他沒有地圖！！！但是幸運的是，他在山腳下發現了一個寶箱。根據經驗判斷（小 A 有經驗嗎？），地圖應該就在其中！

在寶箱上，有三根柱子以及在一根柱子上的?n?個圓盤。小 A 在經過很長時間判斷后，覺得這就是 hanoi 塔！（這都要琢磨）。但是移動是需要時間的，所以小 A 必須要通過制造延壽藥水來完成這項任務。現在，他請你告訴他需要多少步完成，以便他造足夠的延壽藥水。

輸入格式

一個數?n，表示有?n?個圓盤。

輸出格式

一個數?s，表示需要?s?步。

輸入輸出樣例

輸入 #1

31

輸出 #1

2147483647

輸入 #2

15

輸出 #2

32767

說明/提示

數據范圍及約定

對于所有數據，n≤15000。

代碼：

#include <iostream>
#include <vector>using namespace std;int main() {int n;cin >> n;vector<int> digits;digits.push_back(1); // 初始為1，逆序存儲for (int i = 0; i < n; ++i) {int carry = 0;for (int j = 0; j < digits.size(); ++j) {int temp = digits[j] * 2 + carry;digits[j] = temp % 10;carry = temp / 10;}if (carry != 0) {digits.push_back(carry);}}// 減一操作int borrow = 1;for (int i = 0; i < digits.size() && borrow != 0; ++i) {digits[i] -= borrow;if (digits[i] < 0) {digits[i] += 10;borrow = 1;} else {borrow = 0;}}// 去除前導零while (!digits.empty() && digits.back() == 0) {digits.pop_back();}if (digits.empty()) {cout << 0;} else {for (auto it = digits.rbegin(); it != digits.rend(); ++it) {cout << *it;}}cout << endl;return 0;
}

代碼解釋：

代碼邏輯分析

1. 輸入處理

• 讀取整數?n，表示需要計算的次方數。

2. 初始化大數存儲

• 使用動態數組?digits???逆序存儲??大數，初始值為?[1]（即?20=1）。
• 逆序存儲意味著低位在前，高位在后。例如，數值 123 存儲為?[3, 2, 1]。

3. 計算?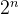

• 通過 ??n?次循環??，每次將當前數值乘以 2。
• ??處理進位??：
  • 遍歷每一位數字，計算?當前位 × 2 + 進位。
  • 更新當前位為結果的個位，進位為十位。
  • 若所有位處理完仍有進位，將其作為新高位加入數組。

??示例??：初始為 1，計算?23=8：

• 第1次循環：1×2 → 2 →?[2]
• 第2次循環：2×2 → 4 →?[4]
• 第3次循環：4×2 → 8 →?[8]

4. 減一操作

• 從最低位開始借位減一：
  • 若當前位減一后為負數，加 10 并設置借位。
  • 否則，直接減一并結束借位。

??示例??：=16?減一：

• 數值 16 存儲為?[6, 1]。
• 減一后，低位 6 → 5，無借位，結果為?[5, 1]（即 15）。

5. 去除前導零

• 逆序存儲中前導零位于數組末尾，需移除。
• 若所有位均為零，最終輸出 0。

6. 輸出結果

• 逆序輸出數組，得到正確的高位到低位順序。

代碼示例解析（以?n=3?為例）

1. ??計算?=8??：
   • 初始?digits = [1]。
   • 3次循環后，digits = [8]（逆序存儲 8）。
2. ??減一??：
   • 8 - 1 = 7?→?digits = [7]。
3. ??輸出??：
   • 逆序輸出?7。

2.?Problem D: 漢諾塔 題解

Description

????????有三根柱A，B，C在柱A上有N塊盤片，所有盤片都是大的在下面，小片能放在大片上面。現要將A上的N塊片移到C柱上，每次只能移動一片，而且在同一根柱子上必須保持上面的盤片比下面的盤片小，請輸出移動的步驟。

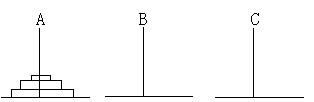
Input

????????輸入整數n，表示有n塊盤片

Output

????????輸出移動的步驟

• Sample Input

3

• Sample Output

1 A->C
2 A->B
3 C->B
4 A->C
5 B->A
6 B->C
7 A->C

HINT

0 < n < 20

代碼：

#include <cstdio>
#include <vector>
#include <string>
#include <cstring>using namespace std;vector<string> steps;
int step = 0;void hanoi(int n, char from, char to, char via) {if (n == 1) {step++;char buffer[20];snprintf(buffer, sizeof(buffer), "%d %c->%c", step, from, to);steps.emplace_back(buffer);} else {hanoi(n - 1, from, via, to);step++;char buffer[20];snprintf(buffer, sizeof(buffer), "%d %c->%c", step, from, to);steps.emplace_back(buffer);hanoi(n - 1, via, to, from);}
}int main() {int n;scanf("%d", &n);steps.reserve((1 << n) - 1); // 預分配足夠內存hanoi(n, 'A', 'C', 'B');// 計算總輸出長度size_t total_len = 0;for (const auto& s : steps) {total_len += s.size() + 1; // 每行加換行符}// 合并到緩沖區并一次性輸出char* buffer = new char[total_len];char* ptr = buffer;for (const auto& s : steps) {size_t len = s.size();memcpy(ptr, s.c_str(), len);ptr += len;*ptr++ = '\n';}fwrite(buffer, 1, total_len, stdout);delete[] buffer;return 0;
}

代碼解釋：

1. ??漢諾塔獨特遞歸算法??：

   • hanoi?函數遞歸地將?n?個盤子從起始柱?from?移動到目標柱?to，借助中間柱?via。
   • 當?n=1?時，直接將盤子從?from?移到?to，記錄步驟。
   • 對于?n>1，分解為三步：
     • 將?n-1?個盤子從?from?移至?via（遞歸調用）。
     • 將第?n?個盤子從?from?移至?to。
     • 將?n-1?個盤子從?via?移至?to（遞歸調用）。

2. ??記錄步驟??：

   • 使用全局變量?steps（vector<string>）存儲每一步操作。
   • 每移動一個盤子，遞增全局變量?step，并用?snprintf?格式化為字符串（如?"1 A->C"）存入?steps。

3. ??性能優化??：

   • ??內存預分配??：steps.reserve((1 << n) - 1)?預分配足夠內存，避免?vector?動態擴容的開銷。
   • ??單次輸出??：計算所有步驟字符串的總長度，合并到連續內存緩沖區，通過?fwrite?一次性輸出，減少頻繁I/O操作的開銷。

4. ??代碼結構??：

   • ??全局變量??：steps?和?step?簡化參數傳遞，但在多線程環境中不安全（此處單線程無問題）。
   • ??遞歸實現??：清晰體現漢諾塔問題分治思想，時間復雜度為 O(2?)。
   • ??輸入輸出??：scanf?讀取盤子數?n，高效輸出避免逐行打印。

??總結??：遞歸解決漢諾塔問題，記錄每一步移動步驟，并通過內存預分配和單次輸出優化性能，適合高效生成并輸出大量步驟的場景。