貪心的本質是選擇每一階段的局部最優，從而達到全局最優。

無固定套路，舉不出反例，就可以試試貪心。

一般解題步驟：

1.將問題分解成若干子問題

2.找出適合的貪心策略

3.求解每一個子問題的最優解

4.將局部最優解堆疊成全局最優解

分發餅干

思路：為了滿足更多的小孩，就不要造成餅干尺寸的浪費，大尺寸的餅干既可以滿足胃口大的孩子，也可以滿足胃口小的孩子，充分利用餅干尺寸喂飽一個，全局最優就是喂飽盡可能多的小孩。可以嘗試使用貪心策略，先將餅干數組和小孩數組進行排序。然后從后向前遍歷小孩數組，用大餅干優先滿足胃口大的，并統計滿足小孩數量。

class Solution{
public:int findContentChildren(vector<int>&g,vector<int>& s){sort(g.begin(),g.end());sort(s.begin(),s.end());int index = s.size() - 1;int result = 0;for(int i = g.size() - 1;i >= 0; i--){if(index >= 0 && s[index] >= g[i]){result++;index--;}}return result;}
};

從代碼中可以看出，index用來控制餅干數組的遍歷，遍歷餅干沒有再起一個循環，而是采用自減的方式，這是常用的技巧。

不可以先遍歷比骨干再遍歷胃口，因為外面for，i是固定移動的，if的index才是符合條件移動的。

?反過來，先滿足胃口小的，從小到大去滿足：

class Solution{
public:int findContentChildren(vector<int>& g,vector<int>&s){sort(g.begin(),g.end());sort(s.begin(),s.end());int index = 0;for(int i = 0; i < size(); i++){if(index < g.size() && g[index] <= s[i]){index++;}}return index;}
};

//思路一
class Solution{public int findContentChildren(int[] g, int[] s){Arrays.sort(g);Arrays.sort(s);int start = 0;int count = 0;for(int i = 0; i < s.length && start < g.length; i++){if(s[i] >= g[start]){start++;count++;}}return count;}
}

class Solution{public int findContentChildren(int[] g,int[] s){Arrays.sort(g);//排序胃口Arrays.sort(s);//排序餅干int count = 0;int start = s.length - 1;//胃口數組長度，從start開始遍歷，倒著遍歷，先考慮胃口大的//遍歷胃口，從大到小for(int index = g.length - 1;index >= 0;index--){if(start >= 0 && g[index] <= s[start]){start--;//從大到小count++;//滿足一個計數+1}}return count;//返回計數}
}

擺動序列

如果連續數字之間的差嚴格地在正數和負數之間交替，則數字序列稱為擺動序列。第一個差（如果存在地話），可能是正數或負數，少于兩個元素的序列也是擺動序列。

給定一個整數序列，返回作為擺動序列的最長子序列的長度。通過從原始序列中刪除一些元素來獲得子序列，剩下的元素保持其原始順序。

思路：

貪心

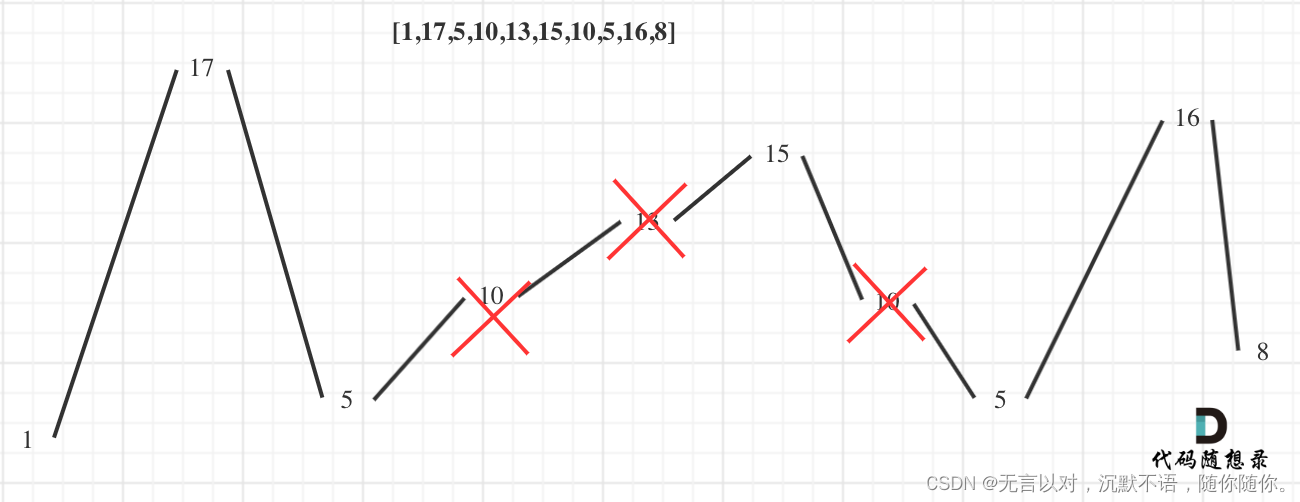
刪除單調坡度上的節點（不包括單調坡度兩端的節點），那么這個坡度就可以有兩個局部峰值。

整體最優：整個序列有最多的局部峰值，從而達到最長擺動序列。

實際操作中，刪除操作都不用，因為題目要求的是最長擺動子序列的長度，所以只需要統計數組的峰值數量就可以了（相當于是刪除單一坡度上的節點，然后統計長度）

這就是貪心所貪的地方，?讓峰值盡可能地保持峰值，然后刪除單一坡度上的節點。

在計算是否有峰值的時候，大家知道遍歷的下標i，計算presiff(nums[i] - nums[i - 1])和curdiff(nums[i + 1] - nums[i]),如果presiff < 0 && surdiff > 0或者prediff > 0 && curdiff < 0，此時就有波動就需要統計。

這是我們思考本題的一個大體思路，但本題還要考慮三種情況：

1.上下坡有平坡

[1，2，2，2，2，1]刪除左邊的三個2，或者刪除右邊的三個2，擺動長度為3

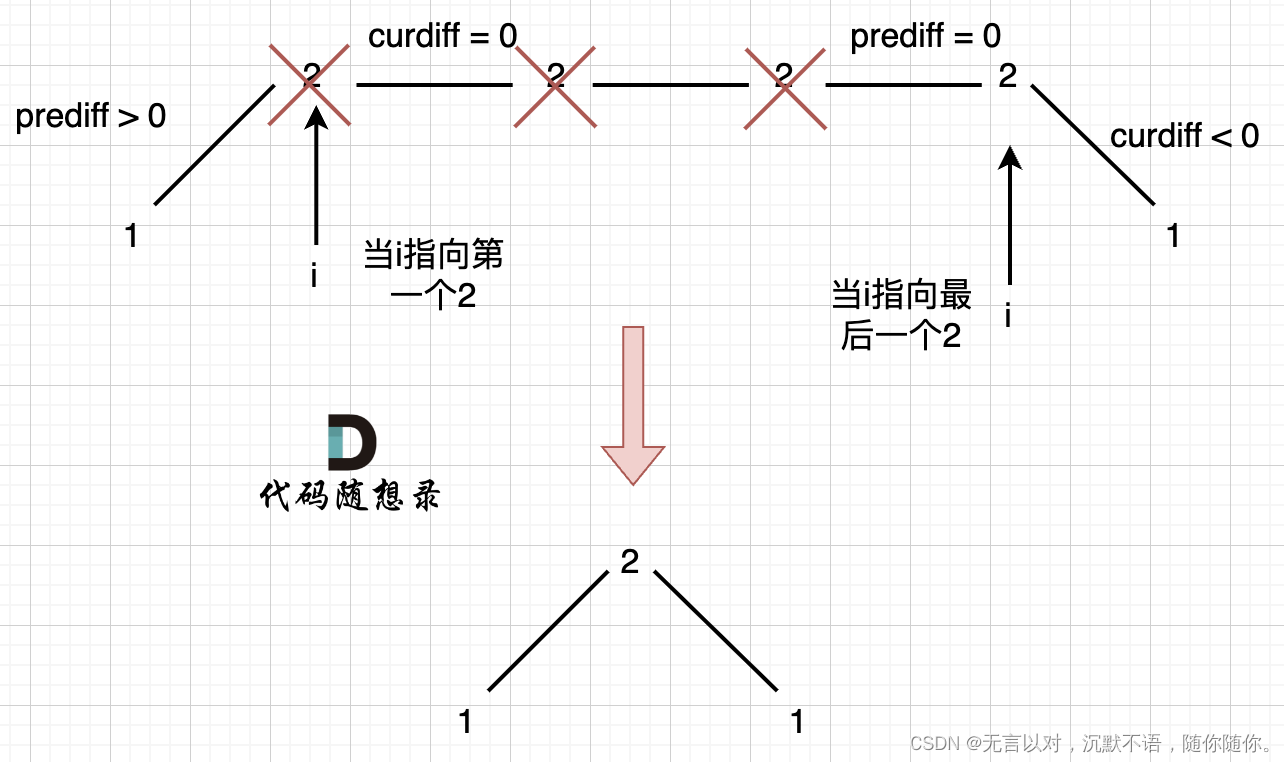
當i指向第一個2的時候，prediff > 0&&curdiff=0，當 i 指向最后一個2的時候，prediff=0 && curdiff <0.

如果采用刪除左面三個2的規則，那么當prediff = 0&&curdiff < 0也要記錄一個峰值，因為他是把之前相同的元素都刪掉留下的峰值。

我們記錄峰值的條件應該是：(preDiff <=0 &&curDiff > 0)||(preDiff >= 0&&curDiff < 0)?

2.數組首尾兩端

本題統計峰值的時候，數組最左面和最右面如何統計。

當有兩個不同的元素時，擺動序列也是2.

例如[2,5],如果靠統計差值來計算峰值個數，就需要考慮數組最左面和最右面的特殊情況。

因為我們在計算prediff（nums[i] - nums[i - 1]）和curdiff(nums[i+1] - nums[i])的時候，至少需要三個數字才能計算，而數組只有兩個數字。這里如果只有兩個數字，且是不同的元素，那結果為2.

3.單調坡中有平坡

之前我們在討論 情況一 ：相同數字練習的時候，prediff = 0，curdiff < 0或者>0也記為波谷

為了統一規則。針對序列[2,5],可以假設為[2,2,5],這樣就有了坡度，即preDiff = 0.

[2,2,5]

針對以上情形，result初始值為1，此時curDiff > 0&&preDiff<=0,那么result++(計算了左面的峰值)，最后得到結果為2（峰值個數為2即擺動序列長度為2）

class Solution{
public:int wiggleMaxLength(vector<int>&nums){if(num.size() <= 1)return nums.size();int curDiff = 0;int preDiff = 0;int result = 1;for(int i = 0; i < nums.size() - 1;i++){curDiff = nums[i + 1]-nums[i];if((preDiff <= 0 &&curDiff >0)||(preDiff >= 0 && curDiff < 0)){result++;}preDiff = curDiff;}};
}

3.在上面解法中，忽略了第三種情況，即如果在一個單調坡度上有平坡，例如[1,2,2,2,3,4]

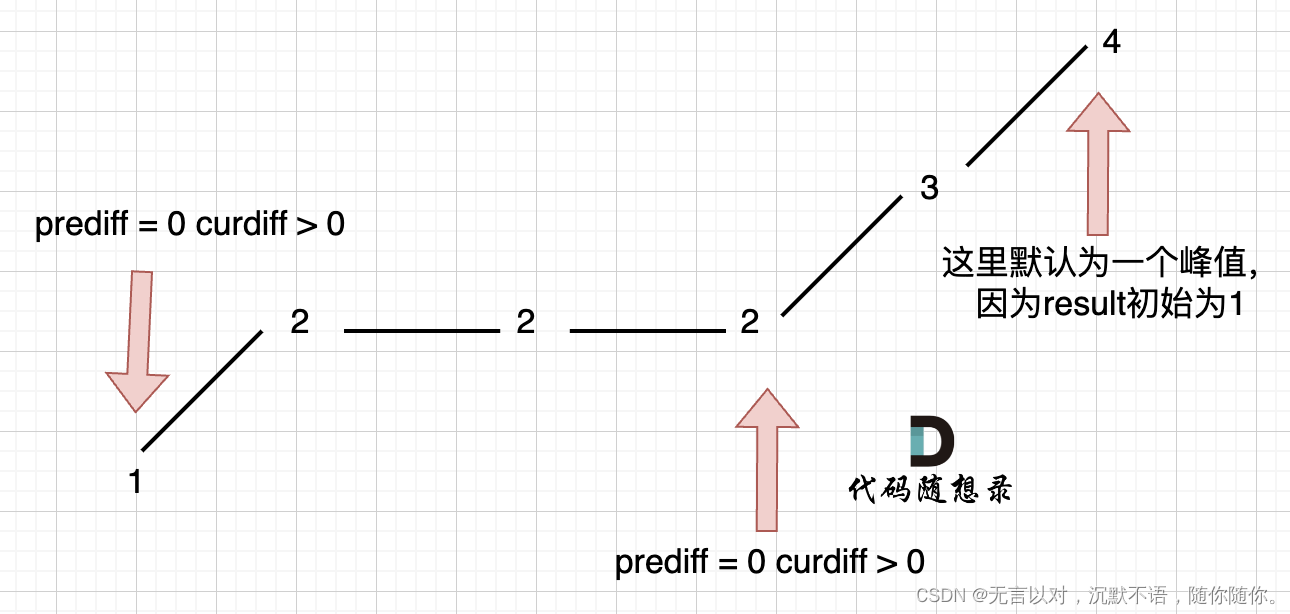
圖中我們可以看出，應該記錄2，單調中的平坡不能算作峰值（擺動）

?需要在坡度擺動變化時，更新prediff，這樣prediff在單調區間有平坡的時候就不會發生變化，造成誤判。

class Solution{
public:int wiggleMaxLength(vctor<int>&nums){if(nums.size() <= 1)return nums.size();int curDiff = 0;int preDiff = 0;int result = 1;for(int i = 0; i < nums.size() - 1;i++){curDiff = nums[i + 1] - nums[i];//出現峰值if((preDiff <= 0 && curDiff > 0)||(preDiff >= 0&& curDiff < 0)){result++;preDiff = curDiff;}}return result;}
};

用動態規劃求解

思路：

對于我們當前考慮的這個數，要么是作為山峰（nums[i] > nums[i - 1]）,要么是作為山谷（即nums[i] < nums[i-1]）

設dp狀態dp[i][0],表示考慮前i個數，第i個數作為山峰的擺動子序列的最長長度。

設dp狀態為dp[i][1],表示考慮前i個數，第i個數作為山谷的擺動子序列的最長長度

則轉移方程為：

dp[i][0] = max(dp[i][0],dp[j][1]? + 1),其中0<j<i且nums[j] < nums[i],表示將