代碼隨想錄二叉樹第四周

617.合并二叉樹?

700.二叉搜索樹中的搜索

98.驗證二叉搜索樹

530.二叉搜索樹的最小絕對差

501.二叉搜索樹中的眾樹

?236.二叉樹的最近公共祖先

617.合并二叉樹?

617. 合并二叉樹

簡單

給你兩棵二叉樹：?root1?和?root2?。

想象一下，當你將其中一棵覆蓋到另一棵之上時，兩棵樹上的一些節點將會重疊（而另一些不會）。你需要將這兩棵樹合并成一棵新二叉樹。合并的規則是：如果兩個節點重疊，那么將這兩個節點的值相加作為合并后節點的新值；否則，不為?null 的節點將直接作為新二叉樹的節點。

返回合并后的二叉樹。

注意:?合并過程必須從兩個樹的根節點開始。

示例 1：

輸入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
輸出：[3,4,5,5,4,null,7]

示例 2：

輸入：root1 = [1], root2 = [1,2]
輸出：[2,2]

提示：

兩棵樹中的節點數目在范圍?[0, 2000]?內
-104 <= Node.val <= 104

遞歸法：

/*** Definition for a binary tree node.* public class TreeNode {*     int val; // 節點值*     TreeNode left; // 左子節點*     TreeNode right; // 右子節點*     TreeNode() {} // 無參構造函數*     TreeNode(int val) { this.val = val; } // 帶值構造函數*     TreeNode(int val, TreeNode left, TreeNode right) { // 帶值和子節點的構造函數*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/// 解題思路：
// 使用遞歸，對兩棵樹的對應節點進行合并，如果其中一個節點為空，則返回另一個節點，否則，將兩個節點的值相加作為新節點的值，
// 然后遞歸合并它們的左右子樹。class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {// 如果兩個根節點都為空，則返回空if (root1 == null && root2 == null) {return null;}// 如果其中一個根節點為空，則返回另一個根節點if (root1 == null && root2 != null) {return root2;}if (root2 == null && root1 != null) {return root1;}// 創建一個新的節點，值為兩個根節點值的和TreeNode node = new TreeNode();node.val = root1.val + root2.val;// 遞歸合并左子樹和右子樹node.left = mergeTrees(root1.left, root2.left);node.right = mergeTrees(root1.right, root2.right);return node; // 返回合并后的根節點}
}

迭代法：?

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {// 如果第一棵樹為空，則返回第二棵樹if(root1 == null){return root2;}// 如果第二棵樹為空，則返回第一棵樹if(root2 == null){return root1;}// 創建一個隊列，用于按層遍歷二叉樹Queue<TreeNode> queue = new LinkedList<>();// 將第一棵樹的根節點和第二棵樹的根節點加入隊列queue.offer(root1);queue.offer(root2);// 循環處理隊列中的節點while(!queue.isEmpty()){// 依次從隊列中取出兩棵樹的節點TreeNode node1 = queue.poll();TreeNode node2 = queue.poll();// 合并兩棵樹的當前節點的值node1.val += node2.val;// 如果兩棵樹的左子節點均不為空，則將左子節點加入隊列if(node1.left != null && node2.left != null){queue.offer(node1.left);queue.offer(node2.left);}// 如果第一棵樹的左子節點為空而第二棵樹的左子節點不為空，則將第二棵樹的左子節點賦給第一棵樹if(node1.left == null && node2.left != null){node1.left = node2.left;}// 如果兩棵樹的右子節點均不為空，則將右子節點加入隊列if(node1.right != null && node2.right != null){queue.offer(node1.right);queue.offer(node2.right);}// 如果第一棵樹的右子節點為空而第二棵樹的右子節點不為空，則將第二棵樹的右子節點賦給第一棵樹if(node1.right == null && node2.right != null){node1.right = node2.right;}}// 返回第一棵樹return root1;}
}

700.二叉搜索樹中的搜索

700. 二叉搜索樹中的搜索

簡單

給定二叉搜索樹（BST）的根節點?root?和一個整數值?val。

你需要在 BST 中找到節點值等于?val?的節點。返回以該節點為根的子樹。如果節點不存在，則返回?null?。

示例 1:

輸入：root = [4,2,7,1,3], val = 2
輸出：[2,1,3]

示例 2:

輸入：root = [4,2,7,1,3], val = 5
輸出：[]

提示：

樹中節點數在?[1, 5000]?范圍內
1 <= Node.val <= 107
root?是二叉搜索樹
1 <= val <= 107

遞歸法：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode searchBST(TreeNode root, int val) {// 如果根節點為空或者根節點的值等于目標值，則返回根節點if(root == null || root.val == val){return root;}// 定義一個用于存儲搜索結果的節點TreeNode node = new TreeNode();// 如果根節點的值小于目標值，則在右子樹中搜索if(root.val < val){node = searchBST(root.right,val);}// 如果根節點的值大于目標值，則在左子樹中搜索if(root.val > val){node = searchBST(root.left,val);}// 返回搜索到的節點return node;}
}

迭代法：?

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode searchBST(TreeNode root, int val) {// 當根節點不為null時，執行循環while(root != null){// 如果根節點的值大于目標值，則繼續在左子樹中搜索if(root.val > val){root = root.left;}// 如果根節點的值小于目標值，則繼續在右子樹中搜索else if(root.val < val){root = root.right;}// 如果根節點的值等于目標值，則返回根節點else{return root;}}// 如果根節點為null，則表示未找到目標值，返回nullreturn root;}
}

98.驗證二叉搜索樹

98. 驗證二叉搜索樹

中等

給你一個二叉樹的根節點?root?，判斷其是否是一個有效的二叉搜索樹。

有效?二叉搜索樹定義如下：

節點的左子樹只包含?小于?當前節點的數。
節點的右子樹只包含?大于?當前節點的數。
所有左子樹和右子樹自身必須也是二叉搜索樹。

示例 1：

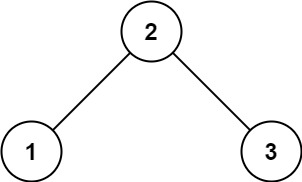
輸入：root = [2,1,3]
輸出：true

示例 2：

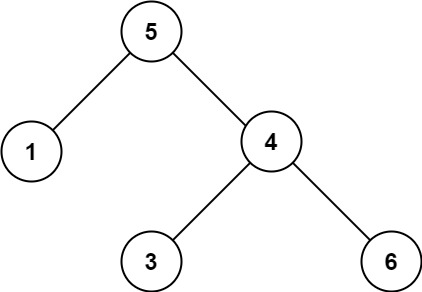
輸入：root = [5,1,4,null,null,3,6]
輸出：false
解釋：根節點的值是 5 ，但是右子節點的值是 4 。

提示：

樹中節點數目范圍在[1, 104]?內
-231 <= Node.val <= 231 - 1

經過中序遍歷的話，二叉搜索樹遍歷的順序，val值是從小到大的，設定一個pre節點，判斷在中序遍歷時，每個節點是否都比前一個節點要大，如果滿足條件即為二叉搜索樹

這里會有一個經常忽略的地方就是只判斷左節點<中節點<右節點,這樣就無法判斷下圖情況

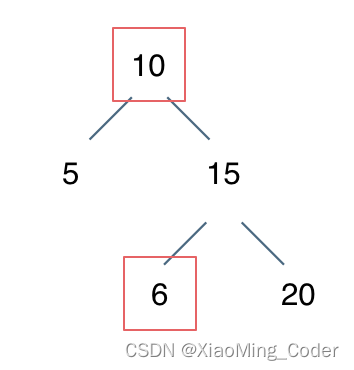
重點在于要明白二叉搜索樹的定義?

遞歸法：（這里的遞歸法思路更清晰）

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 用于保存前一個節點的引用TreeNode pre = null;/*** 判斷給定的二叉樹是否為有效的二叉搜索樹* @param root 給定二叉樹的根節點* @return 如果是有效的二叉搜索樹，則返回true；否則返回false*/public boolean isValidBST(TreeNode root) {// 如果根節點為空，則是有效的二叉搜索樹if(root == null){return true;}// 遞歸判斷左子樹是否為有效的二叉搜索樹boolean leftBoolean = isValidBST(root.left);// 如果前一個節點不為空且前一個節點的值大于等于當前節點的值，則不是有效的二叉搜索樹if(pre != null && pre.val >= root.val){return false;}// 更新前一個節點的引用為當前節點pre = root;// 遞歸判斷右子樹是否為有效的二叉搜索樹boolean rightBoolean = isValidBST(root.right);// 返回左右子樹判斷結果的邏輯與return leftBoolean && rightBoolean;}
}

迭代法：

import java.util.Queue;
import java.util.LinkedList;class Solution {// 迭代方法驗證二叉搜索樹public boolean isValidBST(TreeNode root) {if (root == null) {return true; // 空樹被視為有效的二叉搜索樹}// 使用隊列代替棧，模擬中序遍歷過程Queue<TreeNode> queue = new LinkedList<>();TreeNode pre = null; // 用于保存前一個節點// 當根節點不為空或隊列不為空時，循環執行while (root != null || !queue.isEmpty()) {// 將當前節點的左子樹全部入隊列while (root != null) {queue.add(root);root = root.left; // 移動到左子節點}// 處理當前節點TreeNode front = queue.remove(); // 出隊列if (pre != null && front.val <= pre.val) {return false; // 如果當前節點的值小于等于前一個節點的值，返回 false}pre = front; // 更新前一個節點為當前節點root = front.right; // 處理右子樹，移動到右子節點}return true; // 所有節點都遍歷完成，返回 true，代表是二叉搜索樹}
}

530.二叉搜索樹的最小絕對差

530. 二叉搜索樹的最小絕對差

已解答

簡單

相關標簽

相關企業

給你一個二叉搜索樹的根節點?root?，返回?樹中任意兩不同節點值之間的最小差值?。

差值是一個正數，其數值等于兩值之差的絕對值。

示例 1：

輸入：root = [4,2,6,1,3]
輸出：1

示例 2：

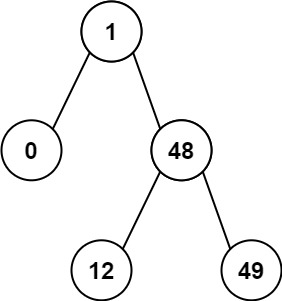
輸入：root = [1,0,48,null,null,12,49]
輸出：1

提示：

樹中節點的數目范圍是?[2, 104]
0 <= Node.val <= 105

class Solution {// 初始化最小差值為整型最大值int minDif = Integer.MAX_VALUE;// 用于保存當前節點的前一個節點TreeNode pre = null;public int getMinimumDifference(TreeNode root) {// 調用輔助方法計算最小差值getMin(root);return minDif;}/*** 輔助方法，遞歸計算二叉搜索樹中任意兩節點值的最小差值。* @param node 當前處理的節點。*/public void getMin(TreeNode node){// 若節點為空，則返回if(node == null){return;}// 遞歸處理左子樹getMin(node.left);// 若前一個節點不為空，則計算當前節點值與前一個節點值的差值，并更新最小差值if(pre != null){minDif = Math.min(minDif, node.val - pre.val);}// 更新前一個節點為當前節點pre = node;// 遞歸處理右子樹getMin(node.right);}
}

501.二叉搜索樹中的眾樹

501. 二叉搜索樹中的眾數

簡單

給你一個含重復值的二叉搜索樹（BST）的根節點?root?，找出并返回 BST 中的所有?眾數（即，出現頻率最高的元素）。

如果樹中有不止一個眾數，可以按?任意順序?返回。

假定 BST 滿足如下定義：

結點左子樹中所含節點的值?小于等于?當前節點的值
結點右子樹中所含節點的值?大于等于?當前節點的值
左子樹和右子樹都是二叉搜索樹

示例 1：

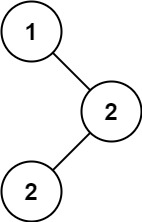
輸入：root = [1,null,2,2]
輸出：[2]

示例 2：

輸入：root = [0]
輸出：[0]

提示：

樹中節點的數目在范圍?[1, 104]?內
-105 <= Node.val <= 105

進階：你可以不使用額外的空間嗎？（假設由遞歸產生的隱式調用棧的開銷不被計算在內）

?暴力解法：使用map集合記錄出現次數，排序后取出最大的

class Solution {public int[] findMode(TreeNode root) {// 創建一個映射表，用于存儲節點值及其出現的頻率Map<Integer, Integer> map = new HashMap<>();// 創建一個列表，用于存儲出現頻率最高的節點值List<Integer> list = new ArrayList<>();// 如果根節點為空，則返回空數組if (root == null) return new int[0];// 獲取樹中節點值的頻率映射searchBST(root, map);// 將映射表中的條目按值的降序排序List<Map.Entry<Integer, Integer>> mapList = new ArrayList<>(map.entrySet());mapList.sort(new Comparator<Map.Entry<Integer, Integer>>() {@Overridepublic int compare(Map.Entry<Integer, Integer> c1, Map.Entry<Integer, Integer> c2) {return c2.getValue().compareTo(c1.getValue());}});// 將出現頻率最高的節點值添加到列表中list.add(mapList.get(0).getKey());// 將與最高頻率相同的節點值也添加到列表中for (int i = 1; i < mapList.size(); i++) {if (mapList.get(i).getValue().equals(mapList.get(i - 1).getValue())) {list.add(mapList.get(i).getKey());} else {break;}}// 將列表轉換為數組并返回int[] result = new int[list.size()];for (int i = 0; i < list.size(); i++) {result[i] = list.get(i);}return result;}// 輔助方法：遍歷二叉搜索樹并更新頻率映射void searchBST(TreeNode curr, Map<Integer, Integer> map) {if (curr == null) return;// 更新節點值的頻率map.put(curr.val, map.getOrDefault(curr.val, 0) + 1);// 遞歸遍歷左子樹和右子樹searchBST(curr.left, map);searchBST(curr.right, map);}}

使用pre指針和當前指針比較，動態更新count，記錄maxCount，更新list中的元素

class Solution {TreeNode pre = null;    // 前一個節點int count = 0;          // 當前節點值的出現次數int maxCount = 0;       // 最大出現次數List<Integer> list = new ArrayList<>(); // 結果列表/*** 查找眾數* @param root 二叉樹的根節點* @return 眾數數組*/public int[] findMode(TreeNode root) {getMode(root);      // 調用獲取眾數的方法int[] result = new int[list.size()];    // 初始化結果數組for(int i = 0; i < list.size(); i++){   // 將結果列表轉換為數組result[i] = list.get(i);}return result;      // 返回結果數組}/*** 獲取眾數* @param root 當前節點*/public void getMode(TreeNode root){if(root == null){   // 如果當前節點為空，直接返回return;}getMode(root.left);     // 遞歸處理左子樹// 如果前一個節點為空，表示當前節點是第一個節點，出現次數初始化為1// 否則，如果當前節點值和前一個節點值相同，出現次數加1，否則重置為1if(pre == null){count = 1;} else if(pre.val == root.val){count ++;} else {count = 1;}// 如果當前節點出現次數等于最大出現次數，則加入結果列表// 如果當前節點出現次數大于最大出現次數，更新最大出現次數和結果列表if(count == maxCount){list.add(root.val);} else if(count > maxCount){maxCount = count;list.clear();list.add(root.val);}pre = root;     // 更新前一個節點getMode(root.right);    // 遞歸處理右子樹}
}

?236.二叉樹的最近公共祖先

236. 二叉樹的最近公共祖先

已解答

中等

相關標簽

相關企業

給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義為：“對于有根樹 T 的兩個節點 p、q，最近公共祖先表示為一個節點 x，滿足 x 是 p、q 的祖先且 x 的深度盡可能大（一個節點也可以是它自己的祖先）。”

示例 1：

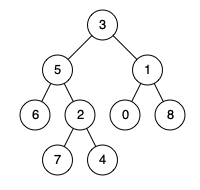
輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出：3
解釋：節點 5 和節點 1 的最近公共祖先是節點 3 。

示例 2：

輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出：5
解釋：節點 5 和節點 4 的最近公共祖先是節點 5 。因為根據定義最近公共祖先節點可以為節點本身。

示例 3：

輸入：root = [1,2], p = 1, q = 2
輸出：1

提示：

樹中節點數目在范圍?[2, 105]?內。
-109 <= Node.val <= 109
所有?Node.val?互不相同?。
p != q
p?和?q?均存在于給定的二叉樹中。

該題分為兩種情況

兩個節點分別存在于公共祖先兩個子樹中

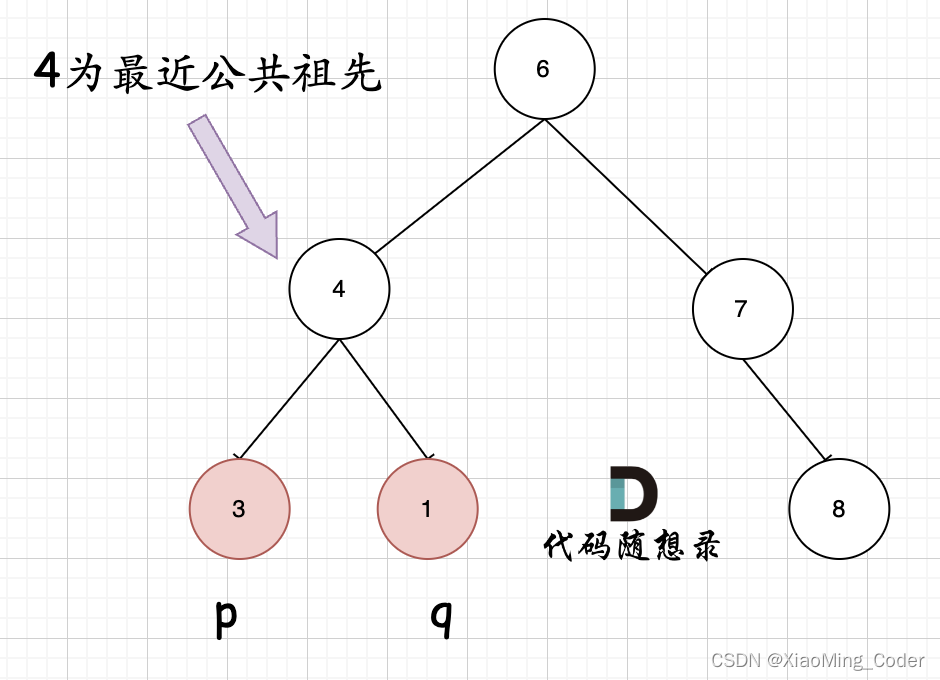
一個節點是另外一個節點的祖先?

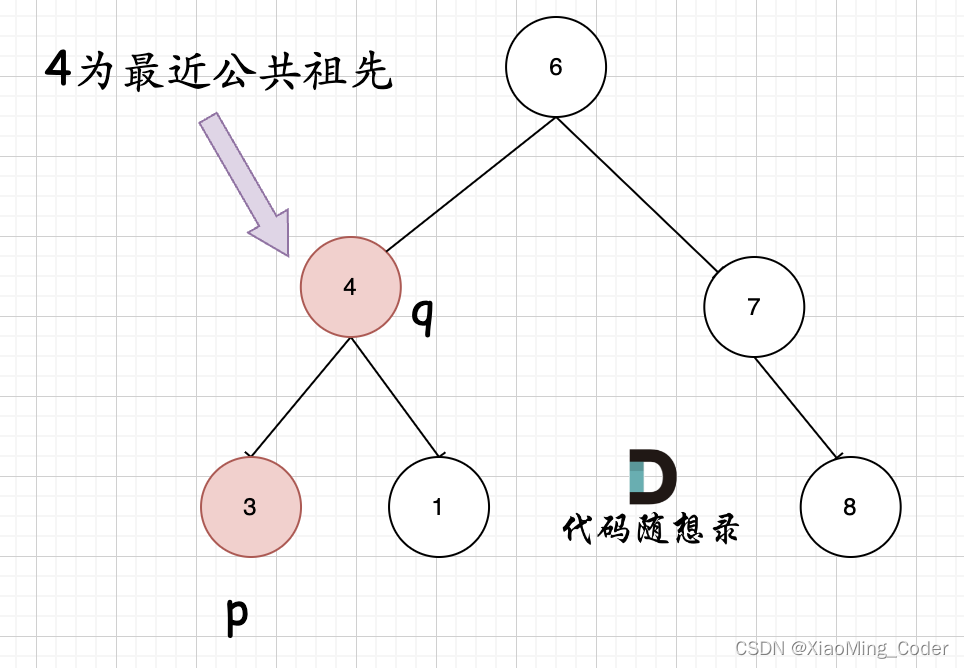
這里我們先依照第一種的情況來解決問題，思路是采用后序遍歷，遇到該兩個節點就向上返回，如果節點兩子樹中都存在返回的節點，表示p，q存在于該節點的兩個子樹中，該節點為最近公共祖先?

class Solution {/*** 尋找兩個節點的最低公共祖先* @param root 根節點* @param p 第一個節點* @param q 第二個節點* @return 最低公共祖先節點*/public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 如果根節點為空，返回 nullif(root == null) {return null;}// 遞歸查找左子樹中的最低公共祖先節點TreeNode leftResult = lowestCommonAncestor(root.left,p,q);// 遞歸查找右子樹中的最低公共祖先節點TreeNode rightResult = lowestCommonAncestor(root.right,p,q);// 如果當前節點為 p 或者 q，則當前節點即為最低公共祖先if(root == p || root == q){return root;}// 如果左子樹和右子樹中均沒有找到公共祖先，則返回 nullif(leftResult == null && rightResult == null){return null;}// 如果左子樹找到了公共祖先，右子樹沒有找到，則返回左子樹中的公共祖先if(leftResult != null && rightResult == null){return leftResult;}// 如果右子樹找到了公共祖先，左子樹沒有找到，則返回右子樹中的公共祖先if(leftResult == null && rightResult != null){return rightResult;}// 如果左右子樹均找到了公共祖先，則當前節點為最低公共祖先else {return root;}}
}

再分析第二種情況，如果一節點是另一個節點的祖先，遞到祖先節點的時候就會返回，歸到根節點返回的是該祖先節點，結果沒有錯誤。