耍雜技的牛

農民約翰的N頭奶牛（編號為1…N）計劃逃跑并加入馬戲團，為此它們決定練習表演雜技。

奶牛們不是非常有創意，只提出了一個雜技表演：

疊羅漢，表演時，奶牛們站在彼此的身上，形成一個高高的垂直堆疊。

奶牛們正在試圖找到自己在這個堆疊中應該所處的位置順序。

這N頭奶牛中的每一頭都有著自己的重量Wi以及自己的強壯程度Si。

一頭牛只撐不住的可能性取決于它頭上所有牛的總重量（不包括它自己）減去它的身體強壯程度的值，現在稱該數值為風險值，風險值越大，這只牛撐不住的可能性越高。

您的任務是確定奶牛的排序，使得所有奶牛的風險值中的最大值盡可能的小。

輸入格式 第一行輸入整數N，表示奶牛數量。

接下來N行，每行輸入兩個整數，表示牛的重量和強壯程度，第i行表示第i頭牛的重量Wi以及它的強壯程度Si。

輸出格式 輸出一個整數，表示最大風險值的最小可能值。

數據范圍

1≤N≤50000, 1≤Wi≤10,000, 1≤Si≤1,000,000,000

輸入樣例：

3 10 3 2 5 3 3

輸出樣例：

2

思路

（貪心）O(nlogn)

與國王游戲的貪心策略相似， 我們先分析

每頭牛的危險值 = 他前面牛的w(重量值)之和 - 自身的s(強壯值)

要使每頭牛的危險值最小，根據貪心思想：

• 自身w值越大應該放到底部（即減小上述式中的被減數）

• 自身s值越大應該放到底部（即增大上述式中的減數）

所以先 假設出一種貪心做法 每頭牛的(w + s)值越大應該排在后面，即升序排序(題見多了可能就會有這種題感)。

接下來進行圖解證明

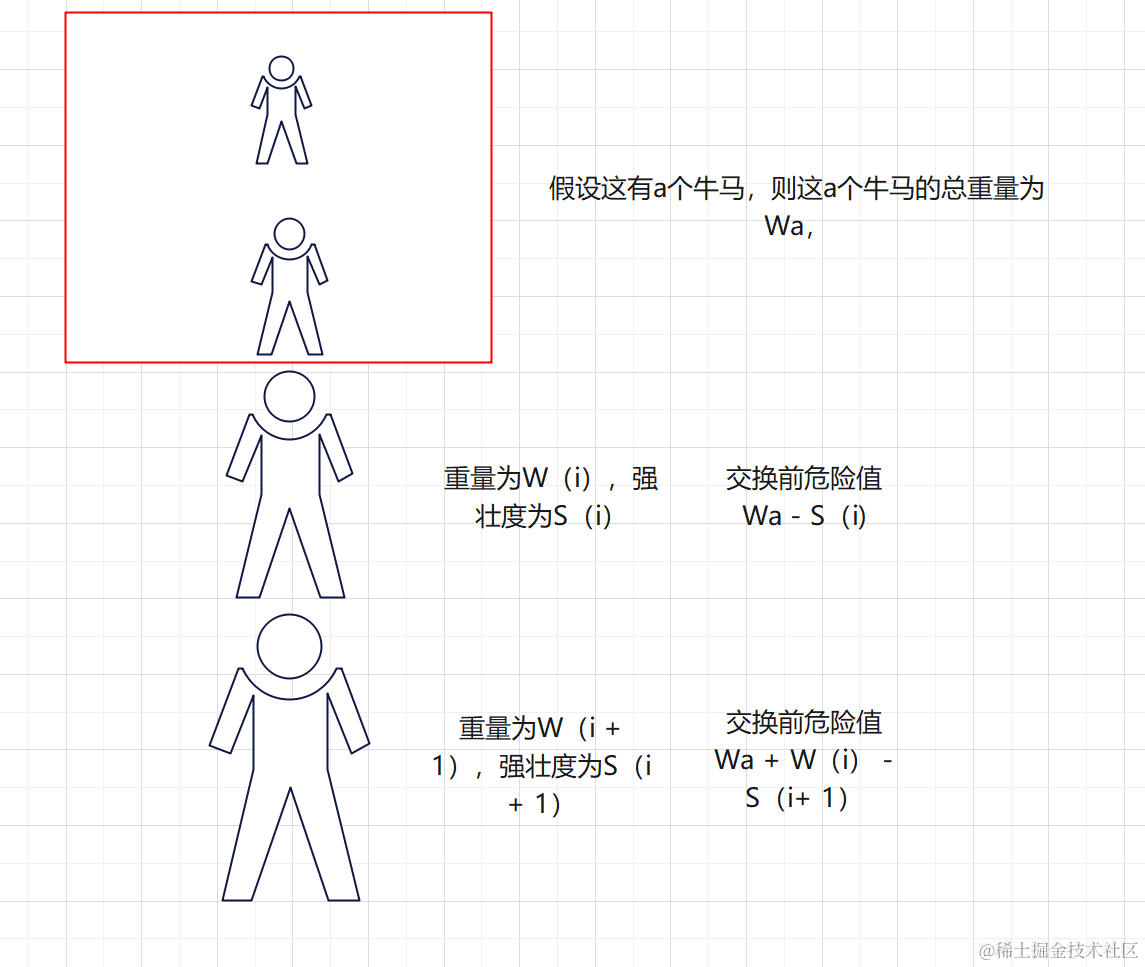
交換前后其他牛的危險值不變

• i之前的牛并不涉及牛i與i+1的重量值，

• i+1之后的牛只涉及到牛i與i+1重量值的和，

所以分析交換前后最大的危險值即可。

我們只需要找到 ：交換前這倆牛馬的危險值的最大值 < 交換后該牛馬的危險值的最大值的條件 ,只要證明在該條件下這四個值的最大值如果是交換后的即可。

現在我們來比較一下

• Wa -S（i + 1）< Wa + W（i)- S（i+1）
• Wa +W（i+ 1） - S（i) > Wa - S（i)

排除倆個，再比較 Wa +W（i+ 1） - S（i) 和Wa + W（i)- S（i+1）

也就是比較W(i) - S(i + 1)（交換前 ） 和W（i + 1) - S（i）（交換后）

如果交換前危險值 > 交換后危險值

W(i) - S(i + 1)（交換前 ） > W（i + 1) - S（i）（交換后）

也就是 W（i） + S（i) > W(i + 1) + S (i + 1)

如果交換前危險值 < 交換后危險值

W(i) - S(i + 1)（交換前 ） < W（i + 1) - S（i）（交換后）

也就是 W（i） + S（i) < W(i + 1) + S (i + 1)

所以得到做法: 按每頭牛的 w + s 進行排序,

當存在逆序時就進行交換(即升序排序)，

import java.util.*;
?
public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();Pair[] pairs = new Pair[n];for(int i = 0; i < n; i ++) {int w = sc.nextInt();int s = sc.nextInt();pairs[i] = new Pair(w, s);}Arrays.sort(pairs, 0, n);int max = Integer.MIN_VALUE;int w = 0;for(int i = 0; i < n; i ++) {int x = w - pairs[i].v;if(x > max) max = x;w += pairs[i].w; ? ? ? ? ? ?}System.out.println(max);}
}
?
?
class Pair implements Comparable<Pair>{
?int w;int v;public Pair(int w, int v) {this.w = w;this.v = v;}public int compareTo(Pair o){return Integer.compare(w + v, o.w + o.v);}}
?