最短路徑（2.19）

目錄

1.網絡延遲時間

弗洛伊德算法

迪杰斯特拉算法

2.?K 站中轉內最便宜的航班

3.從第一個節點出發到最后一個節點的受限路徑數

4.到達目的地的方案數

1.網絡延遲時間

有?n?個網絡節點，標記為?1?到?n。

給你一個列表?times，表示信號經過?有向?邊的傳遞時間。?times[i] = (ui, vi, wi)，其中?ui?是源節點，vi?是目標節點，?wi?是一個信號從源節點傳遞到目標節點的時間。

現在，從某個節點?K?發出一個信號。需要多久才能使所有節點都收到信號？如果不能使所有節點收到信號，返回?-1?。

示例 1：

?

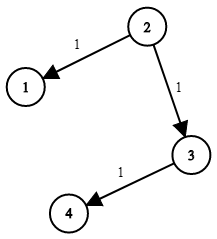
輸入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
輸出：2

示例 2：

輸入：times = [[1,2,1]], n = 2, k = 1
輸出：1

示例 3：

輸入：times = [[1,2,1]], n = 2, k = 2
輸出：-1

提示：

  • 1 <= k <= n <= 100
  • 1 <= times.length <= 6000
  • times[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 0 <= wi <= 100
  • 所有?(ui, vi)?對都?互不相同（即，不含重復邊）

分析：要求最快能到達所有點，就是要找到這個點到達所有點的最短路徑的最大值，用弗洛伊德算法的話就是比較暴力了，算出來所有的以后在需要的頂點找最大值，但是迪杰斯特拉算法少一層循環，只要這個頂點到記錄到所有頂點的最小距離就好?

弗洛伊德算法用鄰接矩陣的時候，可以直接在鄰接矩陣上操作，不用再利用結構體去建圖

弗洛伊德算法

分析：要更新鄰接矩陣，需要一個中間點，寫在三層循環的最外層

#include <bits/stdc++.h>
using namespace std;
main()
{//接受數據int arc,n;cin>>n>>arc;int i,j,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;}cin>>a;a=a-1;//三層循環for(b=0; b<n; b++){for(i=0; i<n; i++){for(j=0; j<n; j++)s[i][j]=min(s[i][j],s[i][b]+s[b][j]);}}int ans=0;for(i=0; i<n; i++)ans=max(ans,s[a][i]);
//    for(i=0; i<n; i++)
//    {
//        for(j=0; j<n; j++)
//            cout<<s[i][j]<<" ";
//        cout<<endl;
//    }ans=ans>9999?-1:ans;cout<<ans;}

迪杰斯特拉算法

分析：找到了一個講迪杰斯特拉算法的文章，講的挺詳細的【C++】Dijkstra算法_dijkstra c++-CSDN博客

先從鄰接矩陣開始寫，要設置好visit[]（做標記）和dist[]（記錄最短距離），從0開始循環n遍，保證每個點都可以做一次中間點，找到最短的且未被標記的，然后以她作為中間點更新

#include <bits/stdc++.h>
using namespace std;
main()
{//接收數據int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;}for(i=0; i<n; i++){for(j=0; j<n; j++){cout<<s[i][j]<<" ";}cout<<endl;}cin>>a;//迪杰斯特拉int visit[n],dist[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));dist[a-1]=0;dist[-1]=9999;//循環n遍for(i=0; i<n; i++){j=-1;//計算最小for(k=0; k<n; k++){if(!visit[k]&&dist[k]<=dist[j])j=k;}//做標記visit[j]=1;//更新路徑for(k=0; k<n; k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}for(k=0;k<n;k++) cout<<dist[k]<<" ";cout<<endl;}int ans=0;for(i=0; i<n; i++){ans=max(ans,dist[i]);}ans=ans>9999?-1:ans;cout<<ans;}

2.?K 站中轉內最便宜的航班

有?n?個城市通過一些航班連接。給你一個數組?flights?，其中?flights[i] = [fromi, toi, pricei]?，表示該航班都從城市?fromi?開始，以價格?pricei?抵達?toi。

現在給定所有的城市和航班，以及出發城市?src?和目的地?dst，你的任務是找到出一條最多經過?k?站中轉的路線，使得從?src?到?dst?的?價格最便宜?，并返回該價格。 如果不存在這樣的路線，則輸出?-1。

示例 1：

輸入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
輸出: 200
解釋: 
城市航班圖如下
?

從城市 0 到城市 2 在 1 站中轉以內的最便宜價格是 200，如圖中紅色所示。

示例 2：

輸入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
輸出: 500
解釋: 
城市航班圖如下
?從城市 0 到城市 2 在 0 站中轉以內的最便宜價格是 500，如圖中藍色所示。

提示：

  • 1 <= n <= 100
  • 0 <= flights.length <= (n * (n - 1) / 2)
  • flights[i].length == 3
  • 0 <= fromi, toi < n
  • fromi != toi
  • 1 <= pricei <= 104
  • 航班沒有重復，且不存在自環
  • 0 <= src, dst, k < n
  • src != dst

分析：我想到的時用迪杰斯特拉算法，在計算的過程中記錄中轉次數進行剪枝,比較容易出錯的點就是可以中專k次，但是直接到達的算是中轉0次，但是如果是原點和終點在同一個地方的話要比0次少一次，那就是-1次，但是我設置的是從原點到原點是0次，所以可以理解成到達某個地方需要乘坐幾次航班，那就是乘坐k+1次時才算中轉k次，這里比較容易出錯

#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a][b]=c;}
//    for(i=0; i<n; i++)
//    {
//        for(j=0; j<n; j++)
//        {
//            cout<<s[i][j]<<" ";
//        }
//        cout<<endl;
//    }cin>>a>>b>>c;int visit[n],dist[n],ans[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(ans,0,sizeof(ans));dist[a]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){if(dist[k]>dist[j]+s[j][k] && ans[j]+1<=c+1){ans[k]=ans[j]+1;dist[k]=dist[j]+s[j][k];}}}//   for(i=0;i<n;i++) cout<<ans[i]<<" ";cout<<dist[b];
}

3.從第一個節點出發到最后一個節點的受限路徑數

現有一個加權無向連通圖。給你一個正整數?n?，表示圖中有?n?個節點，并按從?1?到?n?給節點編號；另給你一個數組?edges?，其中每個?edges[i] = [ui, vi, weighti]?表示存在一條位于節點?ui?和?vi?之間的邊，這條邊的權重為?weighti?。

從節點?start?出發到節點?end?的路徑是一個形如?[z0, z1, z2, ..., zk]?的節點序列，滿足?z0 = start?、zk = end?且在所有符合?0 <= i <= k-1?的節點?zi?和?zi+1?之間存在一條邊。

路徑的距離定義為這條路徑上所有邊的權重總和。用?distanceToLastNode(x)?表示節點?n?和?x?之間路徑的最短距離。受限路徑?為滿足?distanceToLastNode(zi) > distanceToLastNode(zi+1)?的一條路徑，其中?0 <= i <= k-1?。

返回從節點?1?出發到節點?n?的?受限路徑數?。由于數字可能很大，請返回對?109 + 7?取余?的結果。

示例 1：

?

輸入：n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
輸出：3
解釋：每個圓包含黑色的節點編號和藍色的 distanceToLastNode 值。三條受限路徑分別是：
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

示例 2：

?

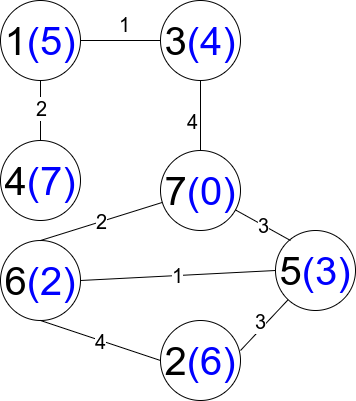
輸入：n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
輸出：1
解釋：每個圓包含黑色的節點編號和藍色的 distanceToLastNode 值。唯一一條受限路徑是：1 --> 3 --> 7 。

提示：

  • 1 <= n <= 2 * 104
  • n - 1 <= edges.length <= 4 * 104
  • edges[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= weighti <= 105
  • 任意兩個節點之間至多存在一條邊
  • 任意兩個節點之間至少存在一條路徑

分析：這個是要先算出各個點到n點的最短路徑，這個的話就應該是迪杰斯特拉算法了，然后放在dist[]中記錄，然后就要搜索所有的路徑根據dist[]的要求去剪枝，這種搜索的話我想到的是回溯，如果這條路可以走的話進行剪枝，但是我看題解好像更多人用的是動態規劃?，直接用dp[]表示1到i的受限路徑數，這樣會簡單很多，這樣放一起來想的話，回溯更適合那種要求寫出路徑的，像這種只求路徑數的更適合動態規劃

#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=9999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;s[b-1][a-1]=c;}
//    for(i=0; i<n; i++)
//    {
//        for(j=0; j<n; j++)
//        {
//            cout<<s[i][j]<<" ";
//        }
//        cout<<endl;
//    }int visit[n],dist[n],dp[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(dp,0,sizeof(dp));dist[n-1]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}}
//    for(i=0;i<n;i++) cout<<dist[i]<<" ";cout<<endl;dp[0]=1;for(i=0;i<n;i++){for(j=i+1;j<n;j++){if(s[i][j]!=9999 && dist[i]>dist[j])dp[j]=dp[j]+dp[i];}for(k=0;k<n;k++) cout<<dp[k]<<" ";cout<<endl;}
//    for(i=0;i<n;i++) cout<<dp[i]<<" ";cout<<endl;cout<<dp[n-1];
//7 8
//1 3 1
//4 1 2
//7 3 4
//2 5 3
//5 6 1
//6 7 2
//7 5 3
//2 6 4}

4.到達目的地的方案數

你在一個城市里，城市由?n?個路口組成，路口編號為?0?到?n - 1?，某些路口之間有?雙向?道路。輸入保證你可以從任意路口出發到達其他任意路口，且任意兩個路口之間最多有一條路。

給你一個整數?n?和二維整數數組?roads?，其中?roads[i] = [ui, vi, timei]?表示在路口?ui?和?vi?之間有一條需要花費?timei?時間才能通過的道路。你想知道花費?最少時間?從路口?0?出發到達路口?n - 1?的方案數。

請返回花費?最少時間?到達目的地的?路徑數目?。由于答案可能很大，將結果對?109 + 7?取余?后返回。

示例 1：

?

輸入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
輸出：4
解釋：從路口 0 出發到路口 6 花費的最少時間是 7 分鐘。
四條花費 7 分鐘的路徑分別為：
- 0 ? 6
- 0 ? 4 ? 6
- 0 ? 1 ? 2 ? 5 ? 6
- 0 ? 1 ? 3 ? 5 ? 6

示例 2：

輸入：n = 2, roads = [[1,0,10]]
輸出：1
解釋：只有一條從路口 0 到路口 1 的路，花費 10 分鐘。

提示：

  • 1 <= n <= 200
  • n - 1 <= roads.length <= n * (n - 1) / 2
  • roads[i].length == 3
  • 0 <= ui, vi <= n - 1
  • 1 <= timei <= 109
  • ui != vi
  • 任意兩個路口之間至多有一條路。
  • 從任意路口出發，你能夠到達其他任意路口。

分析：我剛開始只想到了要用迪杰斯特拉算法計算出最小路徑，然后再用動態規劃計算路徑數目，但是到計算路徑數目的時候被難到了，總想著要用回溯去找路徑，后來看了別人的題解才的發現有一個性質是：如果是合法路徑，那么在途中經過的每一個點都是以最短路徑的方式到達的，也就是說，走到這里消費的時間其實就是dist[i]

那么就可以用dp[i]記錄走到這里等于dist[i]的數目，然后更新dp[i]

#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=9999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a][b]=c;s[b][a]=c;}
//    for(i=0; i<n; i++)
//    {
//        for(j=0; j<n; j++)
//        {
//            cout<<s[i][j]<<" ";
//        }
//        cout<<endl;
//    }int visit[n],dist[n],dp[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(dp,0,sizeof(dp));dist[0]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}}
//    for(i=0;i<n;i++) cout<<dist[i]<<" ";cout<<endl;dp[0]=1;for(i=0;i<n;i++){for(j=i+1;j<n;j++){if(s[i][j]!=9999 && dist[j]==dist[i]+s[i][j])dp[j]=dp[j]+dp[i];}
//            for(k=0;k<n;k++) cout<<dp[k]<<" ";
//            cout<<endl;}
//    for(i=0;i<n;i++) cout<<dp[i]<<" ";cout<<endl;cout<<dp[n-1];
//7 10
//0 6 7
//0 1 2
//1 2 3
//1 3 3
//6 3 3
//3 5 1
//6 5 1
//2 5 1
//0 4 5
//4 6 2}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/718516.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/718516.shtml
英文地址，請注明出處：http://en.pswp.cn/news/718516.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

day32貪心算法 part02

day32貪心算法 part02

貪心系列的時候&#xff0c;題目和題目之間貌似沒有什么聯系,是真的就是沒什么聯系&#xff0c;因為貪心無套路,沒有個整體的貪心框架解決一系列問題&#xff0c;只能是接觸各種類型的題目鍛煉自己的貪心思維。貪心只是一類題的統稱&#xff0c;并沒有什么固定套路。 122. 買賣…
閱讀更多...
Android NDK底層BUG，記錄：connect、socket(AF_INET, SOCK_STREAM, 0) 等系統套接字接口函數崩潰問題。

Android NDK底層BUG，記錄：connect、socket(AF_INET, SOCK_STREAM, 0) 等系統套接字接口函數崩潰問題。

在 Android NDK 之中&#xff0c;看上去調用 connect、socket 函數是不會崩潰的&#xff0c;但這是否定的&#xff0c;它在特定的情況下存在必定的崩潰的問題。 但是這種情況放到MACOS、LINUX、WINDOWS都不會崩潰&#xff0c;而它崩潰的點出現在操作系統底層。 人們需要參考這…
閱讀更多...
香橙派企業信用問題-勸一個是一個，別買！！！

香橙派企業信用問題-勸一個是一個，別買！！！

1. 背景 香橙派推廣旗下AI PRO 開發板&#xff0c;在B站做直播&#xff0c;一場直播兩個直播間&#xff0c;分別抽取一名觀眾&#xff0c;宣傳是場場送AI PRO開發板&#xff01;&#xff01;&#xff01; 2. 收到獎品與宣傳不符合 3.咨詢群主&#xff1a;態度很傲慢&#xff0c…
閱讀更多...
MES的生產計劃管理與ERP的生產計劃管理到底有什么不同？

MES的生產計劃管理與ERP的生產計劃管理到底有什么不同？

在制造業信息化的道路上&#xff0c;ERP系統和MES系統是兩個非常重要的信息化管理工具。大多數制造業企業往往首先考慮上ERP系統&#xff0c;經過一段時間的深度使用后&#xff0c;再引進MES系統進行報工或數采。但我們可以發現&#xff0c;這兩個系統都能進行生產管理&#xf…
閱讀更多...
數學建模團隊分工建議

數學建模團隊分工建議

文章目錄 引言數學建模概述數學建模團隊的組成與角色定位一、團隊組成與角色定位1.1 團隊成員1.2 角色定位 二、團隊協作方式 分工方案分工原則分工策略 按照任務流程分工數據收集與處理分工模型建立與優化分工結果分析與報告撰寫分工用代碼來表示這個過程 總結模塊目錄模塊一&…
閱讀更多...
詳細了解網絡通信流程、協議組成、編碼方式、數據傳輸方式和途徑、Http 協議的編碼、cookie的使用和提取路徑

詳細了解網絡通信流程、協議組成、編碼方式、數據傳輸方式和途徑、Http 協議的編碼、cookie的使用和提取路徑

詳細了解網絡通信流程、協議組成、編碼方式、數據傳輸方式和途徑、Http 協議的編碼、cookie的使用和提取路徑。 一、網絡通信簡介 現代的網絡傳輸介質以以太網鏈路居多，完整的網絡數據報結構大致如下。傳輸層及其以下的機制由操作系統內核提供，應用層由用戶進程提供，應用程…
閱讀更多...
上位機圖像處理和嵌入式模塊部署（qmacvisual學習1）

上位機圖像處理和嵌入式模塊部署（qmacvisual學習1）

【 聲明&#xff1a;版權所有&#xff0c;歡迎轉載&#xff0c;請勿用于商業用途。 聯系信箱&#xff1a;feixiaoxing 163.com】 雖然我們前面學習了很多的知識點&#xff0c;比如說在windows這邊&#xff0c;用qt寫界面&#xff0c;用opencv寫圖像處理代碼&#xff1b;在linux…
閱讀更多...
二維碼門樓牌管理系統技術服務：構建智慧城市的基石

二維碼門樓牌管理系統技術服務：構建智慧城市的基石

文章目錄 前言一、標準地址設置規則二、門樓牌作為標準地址的法定載體三、二維碼門樓牌管理系統技術服務的優勢與應用前景 前言 在智慧城市建設的浪潮中&#xff0c;二維碼門樓牌管理系統技術服務以其高效、便捷的特性&#xff0c;逐漸成為城市管理的重要工具。本文將深入探討…
閱讀更多...
一張草圖直接生成視頻游戲，谷歌推出生成交互大模型

一張草圖直接生成視頻游戲，谷歌推出生成交互大模型

谷歌DeepMind的研究人員推出了&#xff0c;首個無需數據標記、無監督訓練的生成交互模型——Generative Interactive Environments&#xff0c;簡稱“Genie”。 Genie有110億參數&#xff0c;可以根據圖像、真實照片甚至草圖&#xff0c;就能生成各種可控制動作的視頻游戲。Ge…
閱讀更多...
項目可行性方案：人臉識別實現無感考勤的項目技術可行性方案

項目可行性方案：人臉識別實現無感考勤的項目技術可行性方案

目 錄 1.引言 1.1編寫目的 1.2背景 2.可行性研究的前提 2.1要求 2.2目標 3.對現有系統的分析 3.1系統改進示意圖 3.2改進之處 3.3技術條件方面的可行性 4.結論 1.引言 1.1編寫目的 本報告編寫的目的是探究學校里對教室和辦公室內教師的人臉進行識別從而…
閱讀更多...
Linux --- 應用層 | HTTP | HTTPS

Linux --- 應用層 | HTTP | HTTPS

前言 前面寫的TCP/UDP客戶端在訪問服務端的時候&#xff0c;需要輸入ip地址和端口號才可以訪問&#xff0c; 但在現實中&#xff0c;我們訪問一個網站是直接輸入的一個域名&#xff0c;而不是使用的ip地址端口號。 比如在訪問百度 https://www.baidu.com/的時候&#xff0c; …
閱讀更多...
RocketMQ - 深入研究一下消費者是如何獲取消息處理以及進行ACK

RocketMQ - 深入研究一下消費者是如何獲取消息處理以及進行ACK

1. 消費者組到底是個什么概念 消費者組的意思就是讓你給一組消費者起一個名字，比如有一個Topic叫“TopicOrderPaySuccess”，然后假設有庫存系統、積分系統、營銷系統、倉儲系統他們都要去消費這個Topic中的數據。 此時我們應該給這四個系統分別起一個消費組的名字，比如sto…
閱讀更多...
Linux：管道文件及相關API

Linux：管道文件及相關API

目錄 前言一、管道文件1、基本概念2、匿名(無名)管道3、命名(有名)管道4、管道的特點5、思考&#xff1a;何時只能使用無名管道&#xff0c;何時又只能用有名管道&#xff1f;無名管道&#xff08;匿名管道&#xff09;適用的情況&#xff1a;有名管道&#xff08;命名管道&…
閱讀更多...
2024最新AI系統ChatGPT網站源碼, AI繪畫系統

2024最新AI系統ChatGPT網站源碼, AI繪畫系統

一、前言說明 R5Ai創作系統是基于ChatGPT進行開發的Ai智能問答系統和Midjourney繪畫系統&#xff0c;支持OpenAI-GPT全模型國內AI全模型。本期針對源碼系統整體測試下來非常完美&#xff0c;那么如何搭建部署AI創作ChatGPT&#xff1f;小編這里寫一個詳細圖文教程吧。已支持GP…
閱讀更多...
CVE-2024-23334 AIOHTTP 目錄遍歷漏洞分析

CVE-2024-23334 AIOHTTP 目錄遍歷漏洞分析

漏洞描述&#xff1a; aiohttp 是一個用于 asyncio 和 Python 的異步 HTTP 客戶端/服務器框架。使用aiohttp作為Web服務器并配置靜態路由時&#xff0c;需要指定靜態文件的根路徑。此外&#xff0c;選項“follow_symlinks”可用于確定是否遵循靜態根目錄之外的符號鏈接。當“f…
閱讀更多...
css樣式元素的相對定位，絕對定位，固定定位等元素定位運用技巧詳解

css樣式元素的相對定位，絕對定位，固定定位等元素定位運用技巧詳解

文章目錄 1.相對定位 relative2.絕對定位 absolute3.固定定位4.display 轉換元素5.float浮動6.float產生內容塌陷問題7.overflow CSS樣式學習寶典&#xff0c;關注點贊加收藏&#xff0c;防止迷路哦 在CSS中關于定位的內容是&#xff1a;position:relative | absolute | static…
閱讀更多...
Unreal觸屏和鼠標控制旋轉沖突問題

Unreal觸屏和鼠標控制旋轉沖突問題

Unreal觸屏和鼠標控制旋轉沖突問題 鼠標控制攝像機旋轉添加Input軸計算旋轉角度通過軸事件控制旋轉 問題和原因問題原因 解決辦法增加觸摸控制旋轉代碼觸屏操作下屏蔽鼠標軸響應事件 鼠標控制攝像機旋轉 通過Mouse X和Mouse Y控制攝像機旋轉。 添加Input軸 計算旋轉角度 通過…
閱讀更多...
SpringBootWeb快速入門

SpringBootWeb快速入門

1.創建springboot工程&#xff0c;新建module 2.勾選web開發相關依賴 3.刪除多余文件 4.新建類 5.啟動類中運行main方法 6.啟動 默認端口號8080 7.打開瀏覽器&#xff0c;地址欄輸入 8.報錯 9.原因&#xff0c;控制層位置放錯&#xff0c;剪切controller層放進com.example …
閱讀更多...
[vue error] TypeError: Components is not a function

[vue error] TypeError: Components is not a function

問題詳情 問題描述: element plus按需導入后&#xff0c;啟動項目報錯&#xff1a; 問題原因 unplugin-vue-components插件版本問題 查看 unplugin-vue-components插件可以發現版本太高了 問題解決 unplugin-vue-components 版本高了&#xff0c;我用的0.26.0&#xff0c…
閱讀更多...
AI寫的wordpress網站首頁模板 你覺得怎么樣？

AI寫的wordpress網站首頁模板 你覺得怎么樣？

以下是一個AI寫的基本的首頁模板示例&#xff0c;包含您提到的各個模塊。請注意&#xff0c;這只是一個基本框架&#xff0c;您可能需要根據您的具體需求進行進一步的定制和調整。 <!DOCTYPE html> <html <?php language_attributes(); ?>> <head>&…
閱讀更多...
最新文章

Copyright @ 2022~2023