約簡化,訪客和廣播
- 一、約簡化
- 1. 標準計算
- 2. 布爾約減
- 二、訪問
- 三、部分約簡
- 1. 將部分約減與其他業務相結合
- 四、廣播
- 1. 將廣播與其他業務相結合
一、約簡化
在Eigen中,約簡化是一個接受矩陣或數組并返回單個標量值的函數。最常用的約簡方法之一是.sum(),它返回給定矩陣或數組中所有系數的和。
#include <iostream>
#include <Eigen/Dense>using namespace std;
int main()
{Eigen::Matrix2d mat;mat << 1, 2,3, 4;cout << "Here is mat.sum(): " << mat.sum() << endl;cout << "Here is mat.prod(): " << mat.prod() << endl;cout << "Here is mat.mean(): " << mat.mean() << endl;cout << "Here is mat.minCoeff(): " << mat.minCoeff() << endl;cout << "Here is mat.maxCoeff(): " << mat.maxCoeff() << endl;cout << "Here is mat.trace(): " << mat.trace() << endl;
}//輸出
Here is mat.sum(): 10
Here is mat.prod(): 24
Here is mat.mean(): 2.5
Here is mat.minCoeff(): 1
Here is mat.maxCoeff(): 4
Here is mat.trace(): 5
由函數 trace() 返回的矩陣的軌跡是對角線系數的和,可以等效地計算為 a.diagonal().sum()。
1. 標準計算
向量的(歐幾里得也就是 ?2 )平方范數可以得到 squaredNorm()。它等于向量與自身的點積,也等價于它的系數絕對值的平方和。
Eigen還提供了 norm() 方法,該方法返回 squaredNorm() 的平方根。
這些運算也可以作用于矩陣;在這種情況下,n × p 矩陣被視為大小為 (n * p) 的向量,因此例如 norm() 方法返回 “Frobenius” 或“Hilbert-Schmidt” 范數。我們不討論矩陣 ?2 范數因為它有不同的含義。
如果需要其他與系數相關的 ?p 規范,請使用 lpNorm<p>() 方法。模板參數p可以取特殊值無窮大,如果你想要的是 ?∞ 范數,它是系數絕對值的最大值。
下面的示例演示了這些方法。
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::VectorXf v(2);Eigen::MatrixXf m(2,2), n(2,2);v << -1,2;m << 1,-2,-3,4;std::cout << "v.squaredNorm() = " << v.squaredNorm() << std::endl;std::cout << "v.norm() = " << v.norm() << std::endl;std::cout << "v.lpNorm<1>() = " << v.lpNorm<1>() << std::endl;std::cout << "v.lpNorm<Infinity>() = " << v.lpNorm<Eigen::Infinity>() << std::endl;std::cout << std::endl;std::cout << "m.squaredNorm() = " << m.squaredNorm() << std::endl;std::cout << "m.norm() = " << m.norm() << std::endl;std::cout << "m.lpNorm<1>() = " << m.lpNorm<1>() << std::endl;std::cout << "m.lpNorm<Infinity>() = " << m.lpNorm<Eigen::Infinity>() << std::endl;
}// 輸出
v.squaredNorm() = 5
v.norm() = 2.23607
v.lpNorm<1>() = 3
v.lpNorm<Infinity>() = 2m.squaredNorm() = 30
m.norm() = 5.47723
m.lpNorm<1>() = 10
m.lpNorm<Infinity>() = 4
算子范數:1 范數和 ∞ 范數矩陣算子范數可以很容易地計算如下:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::MatrixXf m(2,2);m << 1,-2,-3,4;std::cout << "1-norm(m) = " << m.cwiseAbs().colwise().sum().maxCoeff()<< " == " << m.colwise().lpNorm<1>().maxCoeff() << std::endl;std::cout << "infty-norm(m) = " << m.cwiseAbs().rowwise().sum().maxCoeff()<< " == " << m.rowwise().lpNorm<1>().maxCoeff() << std::endl;
}// 輸出
1-norm(m) = 6 == 6
infty-norm(m) = 7 == 7
有關這些表達式語法的更多解釋,請參見下文。
2. 布爾約減
下面的約簡操作是對布爾值進行的:
- 如果給定矩陣或數組中的所有系數都為真,則 all() 返回真。
- 如果給定矩陣或數組中至少有一個系數為真,則 any() 返回真。
- count() 返回給定矩陣或數組中求值為true的系數數。
這些操作符通常與 Array 提供的系數比較和相等操作符一起使用。例如,array > 0 是與 array 大小相同的 array,在 array 對應系數為正的位置為 true。因此,(array > 0).all() 測試數組的所有系數是否都為正。這可以從下面的例子中看到:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::ArrayXXf a(2,2);a << 1,2,3,4;std::cout << "(a > 0).all() = " << (a > 0).all() << std::endl;std::cout << "(a > 0).any() = " << (a > 0).any() << std::endl;std::cout << "(a > 0).count() = " << (a > 0).count() << std::endl;std::cout << std::endl;std::cout << "(a > 2).all() = " << (a > 2).all() << std::endl;std::cout << "(a > 2).any() = " << (a > 2).any() << std::endl;std::cout << "(a > 2).count() = " << (a > 2).count() << std::endl;
}//輸出
(a > 0).all() = 1
(a > 0).any() = 1
(a > 0).count() = 4(a > 2).all() = 0
(a > 2).any() = 1
(a > 2).count() = 2
二、訪問
當想要獲得矩陣或數組中系數的位置時,也就是獲取矩陣中的特殊元素的時候。訪問器很有用。最簡單的例子是 maxCoeff(&x,&y) 和 minCoeff(&x,&y),它們可用于查找矩陣或數組中最大或最小系數的位置。
傳遞給訪問者的參數是指向存儲行和列位置的變量的指針。這些變量的類型應該是Index,如下所示:
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::MatrixXf m(2,2);m << 1, 2,3, 4;//get location of maximumEigen::Index maxRow, maxCol;float max = m.maxCoeff(&maxRow, &maxCol);//get location of minimumEigen::Index minRow, minCol;float min = m.minCoeff(&minRow, &minCol);std::cout << "Max: " << max << ", at: " <<maxRow << "," << maxCol << std::endl;std:: cout << "Min: " << min << ", at: " <<minRow << "," << minCol << std::endl;
}//輸出
Max: 4, at: 1,1
Min: 1, at: 0,0
這兩個函數還返回最小或最大系數的值。
三、部分約簡
部分約簡是可以在矩陣或數組上按列或按行操作的約簡,對每列或每行應用約簡操作,并返回具有相應值的列或行向量。使用 colwise() 或 rowwise() 應用部分縮減。
一個簡單的例子是獲取給定矩陣中每列元素的最大值,并將結果存儲在行向量中:
#include <iostream>
#include <Eigen/Dense>using namespace std;
int main()
{Eigen::MatrixXf mat(2,4);mat << 1, 2, 6, 9,3, 1, 7, 2;std::cout << "Column's maximum: " << std::endl<< mat.colwise().maxCoeff() << std::endl;
}//輸出
Column's maximum:
3 2 7 9
同樣的操作可以按行執行:
#include <iostream>
#include <Eigen/Dense>using namespace std;
int main()
{Eigen::MatrixXf mat(2,4);mat << 1, 2, 6, 9,3, 1, 7, 2;std::cout << "Row's maximum: " << std::endl<< mat.rowwise().maxCoeff() << std::endl;
}//輸出
Row's maximum:
9
7
注意,列操作返回一個行向量,而行操作返回一個列向量。
1. 將部分約減與其他業務相結合
也可以使用部分還原的結果進行進一步處理。這里是另一個例子,它找到一個列,其元素的和在一個矩陣中是最大的。使用按列部分約減,可以將其編碼為:
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::MatrixXf mat(2,4);mat << 1, 2, 6, 9,3, 1, 7, 2;Eigen::Index maxIndex;float maxNorm = mat.colwise().sum().maxCoeff(&maxIndex);std::cout << "Maximum sum at position " << maxIndex << std::endl;std::cout << "The corresponding vector is: " << std::endl;std::cout << mat.col( maxIndex ) << std::endl;std::cout << "And its sum is is: " << maxNorm << std::endl;
}//輸出
Maximum sum at position 2
The corresponding vector is:
6
7
And its sum is is: 13
前面的示例通過colwise()訪問器對每個列應用sum()約簡,獲得一個大小為1x4的新矩陣。
因此,如果
![m = [13216792]](https://img-blog.csdnimg.cn/direct/1d9f18ef4636406eb3feb7a8eea9cff6.png)
然后
![m.colwise().sum()=[431311]](https://img-blog.csdnimg.cn/direct/470786501dc64e7787c448521f5f9bb3.png)
最后應用maxCoeff()約簡來獲得找到最大和的列索引,在本例中是列索引2(第三列)。
四、廣播
廣播背后的概念類似于部分約簡,不同之處在于廣播構建了一個表達式,其中矢量(列或行)通過在一個方向上復制來解釋為矩陣。
一個簡單的例子是向矩陣中的每一列添加一個特定的列向量。
這可以通過以下方式實現:
#include <iostream>
#include <Eigen/Dense>using namespace std;
int main()
{Eigen::MatrixXf mat(2,4);Eigen::VectorXf v(2);mat << 1, 2, 6, 9,3, 1, 7, 2;v << 0,1;//add v to each column of mmat.colwise() += v;std::cout << "Broadcasting result: " << std::endl;std::cout << mat << std::endl;
}//輸出
Broadcasting result:
1 2 6 9
4 2 8 3
我們可以用兩種等價的方式來解釋指令mat.colwise() += v。它把向量v加到矩陣的每一列。或者,它可以被解釋為將向量v重復四次以形成一個4乘2的矩陣,然后將其添加到mat中:
![[13216792] +[01010101] =[14226893]。](https://img-blog.csdnimg.cn/direct/711e353c0f5141f28432cee57cc7035c.png)
操作符-=、+和-也可以按列和按行使用。在數組上,我們還可以使用操作符*=、/=、*和/來執行按列或按行計算的系數乘法和除法。這些運算符在矩陣上是不可用的,因為不清楚它們會做什么。如果要將矩陣mat的第0列與v(0)相乘,第1列與v(1)相乘,以此類推,則使用mat = mat * v. asdiagonal()。
重要的是要指出,要按列或按行添加的向量必須是vector類型,而不能是Matrix。如果不滿足這個條件,則會得到編譯時錯誤。這也意味著廣播操作只能在使用矩陣操作時應用于Vector類型的對象。這同樣適用于Array類,其中等價于VectorXf的是ArrayXf。與往常一樣,不應該在同一個表達式中混合使用數組和矩陣。
要按行執行相同的操作,我們可以這樣做:
#include <iostream>
#include <Eigen/Dense>using namespace std;
int main()
{Eigen::MatrixXf mat(2,4);Eigen::VectorXf v(4);mat << 1, 2, 6, 9,3, 1, 7, 2;v << 0,1,2,3;//add v to each row of mmat.rowwise() += v.transpose();std::cout << "Broadcasting result: " << std::endl;std::cout << mat << std::endl;
}//輸出
Broadcasting result: 1 3 8 123 2 9 5
1. 將廣播與其他業務相結合
廣播還可以與其他操作相結合,例如矩陣或數組操作、縮減和部分縮減。
現在已經介紹了廣播、約簡和部分約簡,我們可以深入到一個更高級的例子中,在矩陣m的列中找到向量v的最近鄰居。歐幾里德距離將在這個例子中使用,通過名為squaredNorm()的部分約簡計算歐幾里德距離的平方:
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::MatrixXf m(2,4);Eigen::VectorXf v(2);m << 1, 23, 6, 9,3, 11, 7, 2;v << 2,3;Eigen::Index index;// find nearest neighbour(m.colwise() - v).colwise().squaredNorm().minCoeff(&index);std::cout << "Nearest neighbour is column " << index << ":" << std::endl;std::cout << m.col(index) << std::endl;
}//輸出
Nearest neighbour is column 0:
1
3
完成這項工作的線是
(m.colwise() - v).colwise().squaredNorm().minCoeff(&index);
具體解析如下:
- m.colwise() - v是一個廣播操作,從m的每一列中減去v。這個操作的結果是一個新的矩陣,其大小與矩陣m相同:
![M.colwise () - v=[?10218447?1]](https://img-blog.csdnimg.cn/direct/76ba88a7966044d2842e1335c6d66129.png)
-
(m.colwise() - v).colwise(). squarednorm()是一個部分約簡,按列計算平方范數。這個操作的結果是一個行向量,其中每個系數是m和v中每列之間的歐幾里德距離的平方:
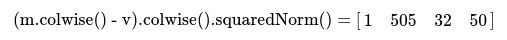
-
最后,使用minCoeff(&index)來獲得m中最接近v的歐氏距離列的索引。
![心法利器[108] | 微調與RAG的優缺點分析](http://pic.xiahunao.cn/心法利器[108] | 微調與RAG的優缺點分析)




 GPIO(1))




)




)


前向傳播、反向傳播和計算圖)
