學習參考：

• 動手學深度學習2.0
• Deep-Learning-with-TensorFlow-book
• pytorchlightning

①如有冒犯、請聯系侵刪。
②已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。
③非常推薦上面（學習參考）的前兩個教程，在網上是開源免費的，寫的很棒，不管是開始學還是復習鞏固都很不錯的。

深度學習回顧，專欄內容來源多個書籍筆記、在線筆記、以及自己的感想、想法，佛系更新。爭取內容全面而不失重點。完結時間到了也會一直更新下去，已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。所有文章涉及的教程都會寫在開頭、一起學習一起進步。

前向傳播用于計算模型的預測輸出，反向傳播用于根據預測輸出和真實標簽之間的誤差來更新模型參數。

前向傳播和反向傳播是神經網絡訓練中的核心步驟，通過這兩個過程，神經網絡能夠學習如何更好地擬合數據，提高預測準確性。

一、計算圖

計算圖（Computational Graph）是一種圖形化表示方法，用于描述數學表達式中各個變量之間的依賴關系和計算流程。在深度學習和機器學習領域，計算圖常用于可視化復雜的數學運算和函數計算過程，尤其是在反向傳播算法中的梯度計算過程中被廣泛應用。

計算圖通常包括兩種節點：

• 計算節點（Compute Nodes）：這些節點表示數學運算，如加法、乘法等。計算節點接受輸入，并產生輸出。
• 數據節點（Data Nodes）：這些節點表示數據或變量，如輸入數據、權重、偏置等。

通過連接計算節點和數據節點的邊，構建了一個有向圖，其中每個節點表示一個操作，邊表示數據流向。計算圖可以幫助理解復雜的計算過程，特別是在深度學習中涉及大量參數和運算的情況下。

二、前向傳播

前向傳播（forward propagation或forward pass） 指的是：按順序（從輸入層到輸出層）計算和存儲神經網絡中每層的結果。

前向傳播（Forward Propagation）：

• 定義：前向傳播是指輸入數據通過神經網絡模型的各層，逐層進行計算并傳遞至輸出層的過程。
• 作用：在前向傳播過程中，輸入數據經過神經網絡的權重和激活函數的計算，最終得到模型的預測輸出。
• 目的：前向傳播的目的是計算模型對輸入數據的預測值，為后續的損失函數計算和反向傳播提供基礎。

1.前向傳播的計算圖

假設單隱藏層神經網絡中，輸入樣本是 𝐱∈? d， 并且隱藏層不包括偏置項。 這里的中間變量是：

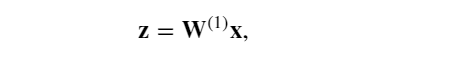
其中 𝐖(1)∈??×𝑑 是隱藏層的權重參數。 將中間變量 𝐳∈?? 通過激活函數 𝜙 后， 得到長度為 ? 的隱藏激活向量是：

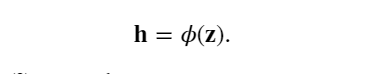
隱藏變量 𝐡也是一個中間變量。 假設輸出層的參數只有權重 𝐖(2)∈?𝑞×?， 可以得到輸出層變量，它是一個長度為 𝑞 的向量：

假設損失函數為 𝑙，樣本標簽為 𝑦，可以計算單個數據樣本的損失項，

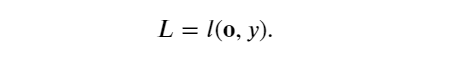
根據 𝐿2 正則化的定義，給定超參數 𝜆 ，正則化項為

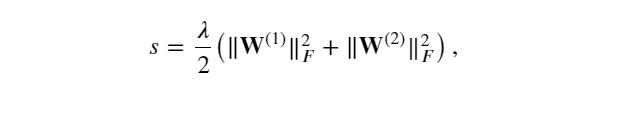
其中矩陣的Frobenius范數是將矩陣展平為向量后應用的 𝐿2范數。 最后，模型在給定數據樣本上的正則化損失為：

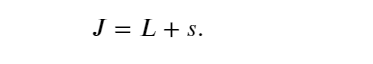
該函數J就是目標函數。

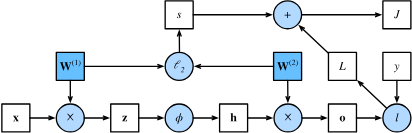
繪制計算圖有助于可視化計算中操作符和變量的依賴關系。

與上述簡單網絡相對應的計算圖， 其中正方形表示變量，圓圈表示操作符。 左下角表示輸入，右上角表示輸出。 注意顯示數據流的箭頭方向主要是向右和向上的。

三、反向傳播

反向傳播（Backpropagation）：

• 定義：反向傳播是指通過計算損失函數對模型參數的梯度（梯度是一個由偏導數組成的向量，表示函數在某一點處的變化率或者斜率方向、也就是在每個自變量方向上的偏導數），從輸出層向輸入層傳播梯度的過程。
• 作用：在反向傳播過程中，根據損失函數計算模型參數的梯度，然后利用梯度下降等優化算法更新模型參數，以減小損失函數的值。
• 目的：反向傳播的目的是根據模型預測與真實標簽的誤差，調整神經網絡中每個參數的值，使模型能夠更好地擬合訓練數據，并提高在新數據上的泛化能力。

反向傳播（backward propagation或backpropagation）指的是計算神經網絡參數梯度的方法。 簡言之，該方法根據微積分中的鏈式規則，按相反的順序從輸出層到輸入層遍歷網絡。 該算法存儲了計算某些參數梯度時所需的任何中間變量（偏導數）。 假設有函數 𝖸=𝑓(𝖷) 和 𝖹=𝑔(𝖸) ， 其中輸入和輸出 𝖷,𝖸,𝖹 是任意形狀的張量。 利用鏈式法則，可以計算 𝖹 關于 𝖷 的導數：

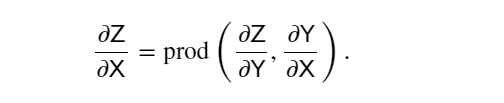
使用 prod 運算符在執行必要的操作（如換位和交換輸入位置）后將其參數相乘。 對于向量，這很簡單，它只是矩陣-矩陣乘法。

在前向傳播的計算圖中，單隱藏層簡單網絡的參數是 𝐖(1) 和 𝐖(2) 。 反向傳播的目的是計算梯度 ?𝐽/?𝐖(1) 和 ?𝐽/?𝐖(2) 。為此，應用鏈式法則，依次計算每個中間變量和參數的梯度。 計算的順序與前向傳播中執行的順序相反，因為需要從計算圖的結果開始，并朝著參數的方向努力。第一步是計算目標函數 𝐽=𝐿+𝑠 相對于損失項 𝐿 和正則項 𝑠 的梯度。

這里為什么等于1？因為單隱藏層簡單網絡的最后一層上面是

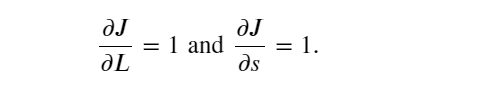
根據鏈式法則計算目標函數關于輸出層變量 𝐨 的梯度：

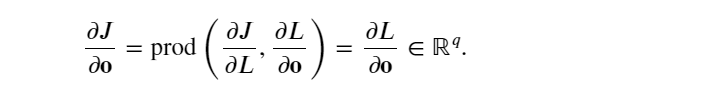
計算正則化項相對于兩個參數的梯度：

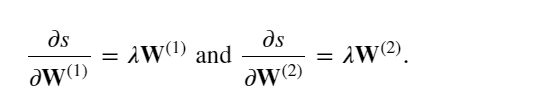
計算最接近輸出層的模型參數的梯度 ?𝐽/?𝐖(2)∈?𝑞×? 。 使用鏈式法則得出：

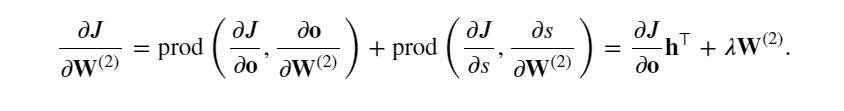
為了獲得關于 𝐖(1)的梯度，需要繼續沿著輸出層到隱藏層反向傳播。 關于隱藏層輸出的梯度 ?𝐽/?𝐡∈?? 由下式給出：

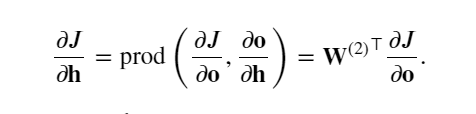
由于激活函數 𝜙 是按元素計算的， 計算中間變量 𝐳的梯度 ?𝐽/?𝐳∈?? 需要使用按元素乘法運算符，用 ⊙ 表示：

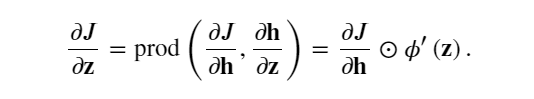
最后，可以得到最接近輸入層的模型參數的梯度 ?𝐽/?𝐖(1)∈??×𝑑 。 根據鏈式法則，我們得到：

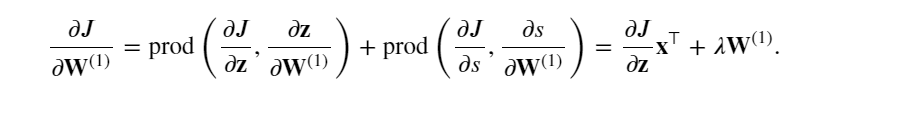
四、訓練神經網絡

在訓練神經網絡時，前向傳播和反向傳播相互依賴。

對于前向傳播，沿著依賴的方向遍歷計算圖并計算其路徑上的所有變量。 然后將這些用于反向傳播，其中計算順序與計算圖的相反。

以上述簡單網絡為例：
正則項：

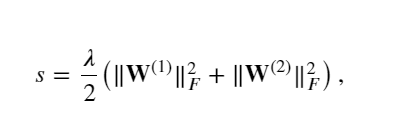
反向傳播中計算J對W(2)的梯度公式：

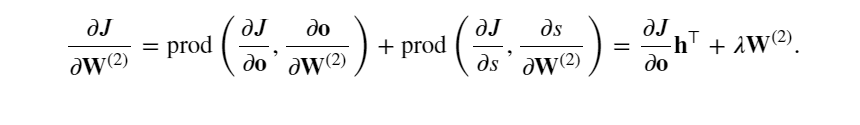
反向傳播中計算J對W(1)的梯度公式：

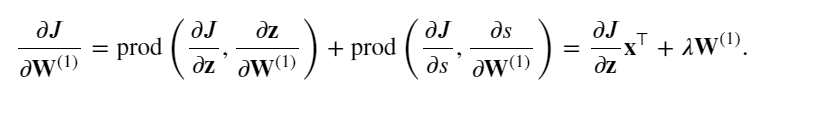
一方面，在前向傳播期間計算正則項取決于模型參數𝐖(1)和 𝐖(2)的當前值。 它們是由優化算法根據最近迭代的反向傳播給出的。 另一方面，反向傳播期間參數的梯度計算， 取決于由前向傳播給出的隱藏變量𝐡的當前值。

因此，在訓練神經網絡時，在初始化模型參數后， 交替使用前向傳播和反向傳播，利用反向傳播給出的梯度來更新模型參數。

注意，反向傳播重復利用前向傳播中存儲的中間值，以避免重復計算。 帶來的影響之一是需要保留中間值，直到反向傳播完成。 這也是訓練比單純的預測需要更多的內存（顯存）的原因之一。 此外，這些中間值的大小與網絡層的數量和批量的大小大致成正比。 因此，使用更大的批量來訓練更深層次的網絡更容易導致內存不足（out of memory）錯誤。