1 B樹介紹

B樹（英語：B-tree），是一種在計算機科學自平衡的樹，能夠保持數據有序。這種數據結構能夠讓查找數據、順序訪問、插入數據及刪除的動作，都在對數時間內完成。B樹，概括來說是一個一般化的二叉搜索樹（binary search tree）一個節點可以擁有2個以上的子節點。與自平衡二叉查找樹不同，B樹適用于讀寫相對大的數據塊的存儲系統，例如磁盤。B樹減少定位記錄時所經歷的中間過程，從而加快訪問速度。B樹這種數據結構可以用來描述外部存儲。這種數據結構常被應用在數據庫和文件系統的實現上。

那為什么要使用 B-樹呢（或者說為啥要有 B-樹呢）？

要解釋清楚這一點，我們假設我們的數據量達到了億級別，主存當中根本存儲不下，我們只能以塊的形式從磁盤讀取數據，與主存的訪問時間相比，磁盤的 I/O 操作相當耗時，而提出 B-樹的主要目的就是減少磁盤的 I/O 操作。大多數平衡樹的操作（查找、插入、刪除，最大值、最小值等等）需要?O(?)?次磁盤訪問操作，其中???是樹的高度。但是對于 B-樹而言，樹的高度將不再是logn(其中 n是樹中的結點個數），而是一個我們可控的高度???（通過調整 B-樹中結點所包含的鍵【你也可以叫做數據庫中的索引，本質上就是在磁盤上的一個位置信息】的數目，使得 B-樹的高度保持一個較小的值）。一般而言，B-樹的結點所包含的鍵的數目和磁盤塊大小一樣，從數個到數千個不等。由于B-樹的高度 h 可控（一般遠小于logn ），所以與 AVL 樹和紅黑樹相比，B-樹的磁盤訪問時間將極大地降低。

平衡二叉排序樹是利用插入的成本緩解查找效率---------->紅黑樹來解決（最長子樹不超過最短子樹的2倍。數據量大的時候，樹會很深，查找次數變多）----------->B樹（多叉，多路查找樹）

動畫顯示樹調整的網站：Data Structure Visualization

2 B樹特點

B樹是一種平衡的多叉樹，通常我們說m階的B樹，它必須滿足如下條件：

• 每個節點最多有m個子節點。
• 每一個非葉子節點（除根節點）最少有[m/2]個子節點。
• 如果根節點不是葉子節點，那么它至少有兩個子節點。
• 有k個子節點的非葉子節點擁有k-1個鍵，且升序排列，滿足k[i] < k[i + 1]
• 每個節點至多包含2*k-1個鍵。
• 所有的葉子節點都在同一層。
• 每個節點的結構是

其中：

n記錄這個節點關鍵字的個數；

P0存儲的是第一個孩子的地址，P1存儲的是第二個孩子的地址，以此類推。。。。。。

K1是第一個關鍵字，K2是第二個關鍵字，以此類推。。。。。。

B樹中一個節點的子節點數目的最大值，用m表示，假如最大值為4，則為4階，如下圖

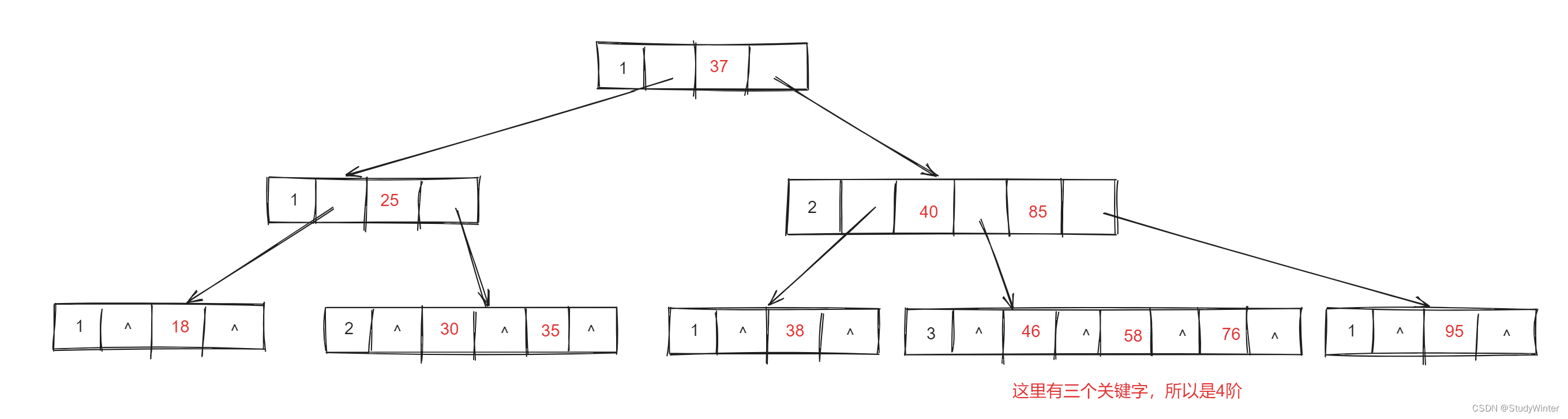
性質：

• 每個節點最多有m個子節點。
• 每一個非葉子節點（除根節點）最少有[m/2]個子節點。
• 如果根節點不是葉子節點，那么它至少有兩個子節點。
• 有k個子節點的非葉子節點擁有k-1個鍵，且升序排列，滿足k[i] < k[i + 1]
• 每個節點至多包含2*k-1個鍵。
• 所有的葉子節點都在同一層。
• 滿足n叉排序樹

3 B樹的增刪改查

磁盤預讀

內存跟磁盤發生數據交互的時候，一般情況下有一個最小的邏輯單元，稱之為頁,datapage

頁一般由操作系統決定是多大，一般是4k或者8k，我們在數據交互時，可以取頁的整數倍來進行讀取。

電腦的文件都是datapage的整數倍

每個節點放在磁盤塊里，用B樹做索引，這個磁盤大小是16k

三層數據。

對比B樹和B+樹

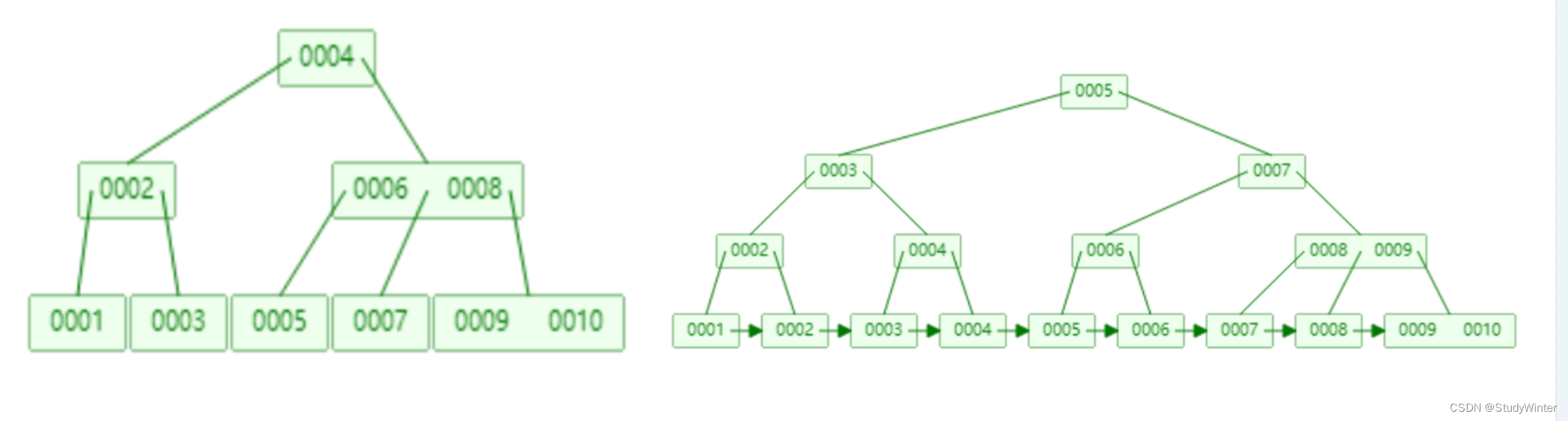
有一個很重要的不同是：B+樹的數據都存在葉子節點上。

參考：

[1]?https://zh.wikipedia.org/zh-hans/B%E6%A0%91

[2]?圖解：什么是B樹？（心中有 B 樹，做人要虛心）一文讀懂B-樹 - 知乎 (zhihu.com)

[3]?B 樹 - OI Wiki (oi-wiki.org)

[4]?終于把B樹搞明白了(四)_B樹的刪除操作_嗶哩嗶哩_bilibili

[5]?notes/docs/B樹和B+樹詳解.md at master · wardseptember/notes · GitHub