1.定義

如果圖$G$(有向圖或者無向圖)中所有邊一次僅且一次行遍所有頂點的通路稱作歐拉通路。

如果圖$G$中所有邊一次僅且一次行遍所有頂點的回路稱作歐拉回路。

具有歐拉回路的圖成為歐拉圖(簡稱$E$圖)。具有歐拉通路但不具有歐拉回路的圖成為半歐拉圖。
頂點可以經過多次
畫個圖分辨一下：

• 歐拉通路：
  
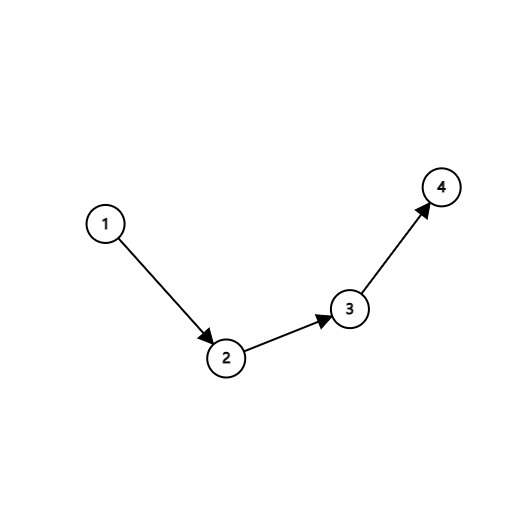
• 歐拉回路
  
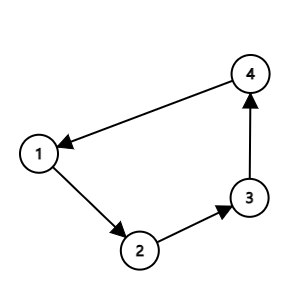
  簡單來講就是歐拉通路能夠從起點到終點,歐拉回路能夠回到起點

2.定理及推論

歐拉通路和歐拉回路的判定是很簡單的
無向圖$G$存在歐拉通路的充要條件是：
$G$為連通圖，并且$G$僅有兩個奇度節點(度數為奇數的頂點)或者無奇度節點
推論1：

1. 當$G$是僅有兩個奇度節點的連通圖時，$G$的歐拉通路必以此兩個節點為端點
2. 當$G$是無奇度節點的連通圖時，$G$必有歐拉回路
3. $G$為歐拉圖(存在歐拉回路)的充分必要條件是$G$為無奇度節點的連通圖

有向圖$D$存在歐拉通路的充要條件是：
$D$為有向圖，$D$的基圖聯通，并且所有頂點的出度與入度都相等；或者除兩個頂點外，其余頂點的出度與入度都相等，而在這兩個頂點中一個頂點的出度與入度只為$1$，另一個頂點的出度與入度之差為$?1$
推論2：

1. $當D除出、入度之差為1，?1的兩個頂點之外，其余頂點的出度與入度都相等時，D的有向歐拉通路必以出、入度之差為1的頂點作為始點，以出、入度之差為?1的頂點作為終點$
2. $當D的所有頂點的出、入度都相等時，D中存在有向歐拉回路$
3. $有向圖D為有向歐拉圖的充分必要條件是D的基圖為連通圖，并且所有的頂點的出、入度都相等$

3.歐拉通路回路存在的判斷

根據定理和推論，我們可以很好的找到歐拉通路回路的判斷方法

A.判斷歐拉通路是否存在的方法#

• $有向圖：圖連通，有一個頂點出度大于入度1，有一個頂點入度大于出度1，其余都是出度=入度$
• 無向圖：圖聯通，只有兩個頂點是奇數度，其余都是偶數度

B.判斷歐拉回路是否存在的方法

• 有向圖：圖聯通，所有的頂點出度=入度
• 無向圖：圖聯通，所有的頂點都是偶數度

4.歐拉回路的應用

1. 哥尼斯堡七橋問題
2. 一筆畫問題
3. 旋轉鼓輪的設計

5.歐拉回路的判斷

$DFS$

鄰接矩陣的時間復雜度為$O(n^2)$
鄰接表的時間復雜度為$O(n+e)$
如果，重邊太多的話，鄰接表會掛掉:）

請看這篇文章

6.歐拉回路的求解

板子題：騎馬修柵欄
傳送門
題目保證有解。

A.DFS搜索求解歐拉回路

基本思路：利用歐拉定理判斷出一個圖存在歐拉回路或歐拉通路后，選擇一個正確的起始頂點，用DFS算法遍歷所有的邊(每條邊只遍歷一次)，遇到走不通就回退。在搜索前進方向上將遍歷過的邊按順序記錄下來。這組邊的排列就組成了一條歐拉通路或回路。

#include <bits/stdc++.h>
using namespace std;
int bian[510],n,m,ans[510];
int mapp[510][510],c=0;
void dfs(int j){for(int i=1;i<=n;i++){if(mapp[j][i]>0){mapp[i][j]--;mapp[j][i]--;dfs(i);}}ans[c++]=j;
}
int main(){cin>>m;int a,b;for(int i=0;i<m;i++){cin>>a>>b;mapp[a][b]++;mapp[b][a]++;bian[a]++;bian[b]++;n=a>n?a:n;n=b>n?b:n;}int flag=1;for(int i=n;i>=1;i--){if(bian[i]%2==1){flag=i;}}dfs(flag);for(int i=c-1;i>=0;i--){cout<<ans[i]<<endl;}
}

B.Fleury(佛羅萊)算法

• Fleury算法是對DFS爆搜的一種改進，使用DFS漫不經心的隨意走效率是不高的，Fleury是一種有效的算法
  ps:其實我也不會,這里就只介紹一下吧
  
  我個人感覺是把大連通塊分成了零散的幾個小連通塊然后分塊連接
  關鍵是能不走橋就不走橋，實在無路可走了才會去走橋
  代碼就不給了,估計給了也是錯的