1. 原理

兩類線性可分的模式類：，設判別函數為：。

　　　　　　　　

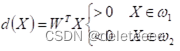
?　　對樣本進行規范化處理，即類樣本全部乘以(-1)，則有：

　　　　　　　　

感知器算法通過對已知類別的訓練樣本集的學習，尋找一個滿足上式的權向量。

2. 過程

2.1 兩類問題感知器算法

首先需要將訓練樣本構造成增廣向量形式然后進行規范化處理，將屬于w2的訓練樣本乘以（-1），處理后的訓練樣本為：

訓練樣本將以列向量的形式儲存在A中，并設初始權向量為（-1，-2，-2，0），矯正量默認為1

接下來通過循環迭代去更新權向量的值（wX<=0則需要修改），代碼如下，設置最大循環次數為100，當某一次迭代過程中八個訓練樣本均判別正確則跳出循環

迭代過程如下：

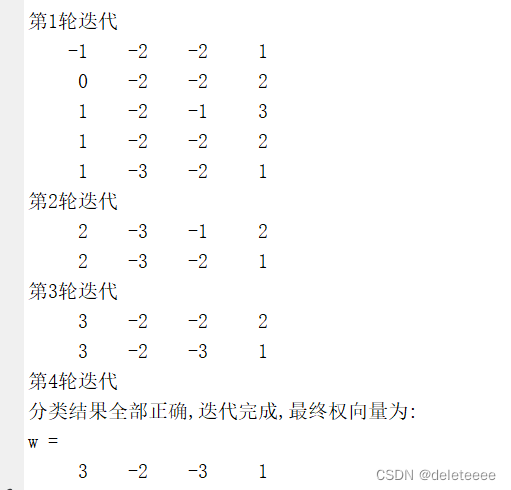
圖1 迭代過程及結果

解向量已經求出，判別函數也就知道了，接下來繪制分類結果及判別界面，繪制三維圖像，其中判別界面可以由內置函數fmesh實現

結果如下：

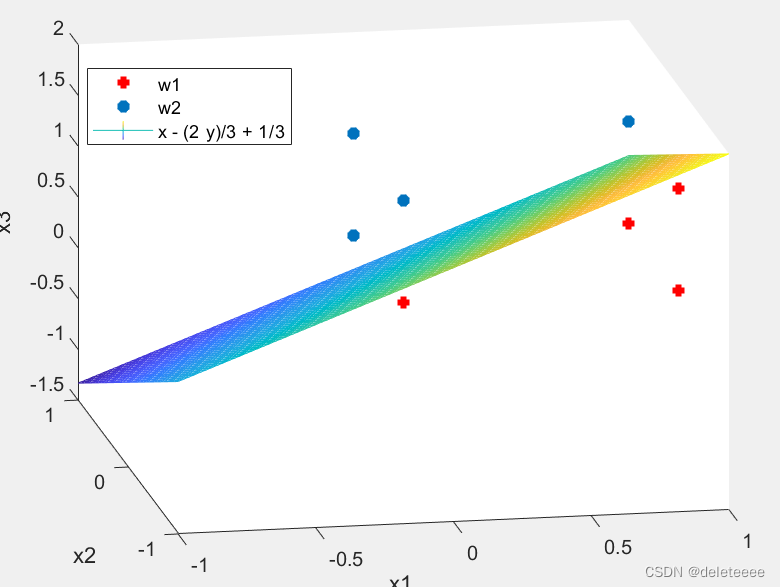
圖2 分類圖和判別界面

2.2 三類問題感知器算法

同樣需要將訓練樣本修改為增廣向量形式，但不需要再乘以（-1），處理結果如下：

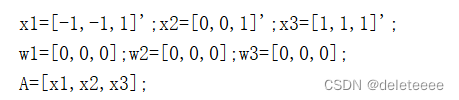
三個初始權向量均設為0向量

設置最大循環次數為100開始進行迭代，每一次迭代需要對三類樣本均判斷比較d1，d2，d3的大小關系并更新權向量的值，以下代碼以第一類樣本為例，滿足條件則更新相應的權向量

迭代過程如下：

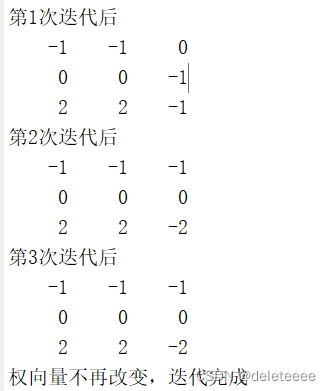
圖3 迭代過程

從中可以看出實際在第二輪迭代中就已經可以獲得結果，第三輪只是進一步驗證

得到了權向量便可以繪制判別函數，由于訓練樣本為2維數據且判別函數可以用直線描述，故可以直接通過兩點一線的方法繪制圖像，由于w2為0向量便無需繪制，結果如下：

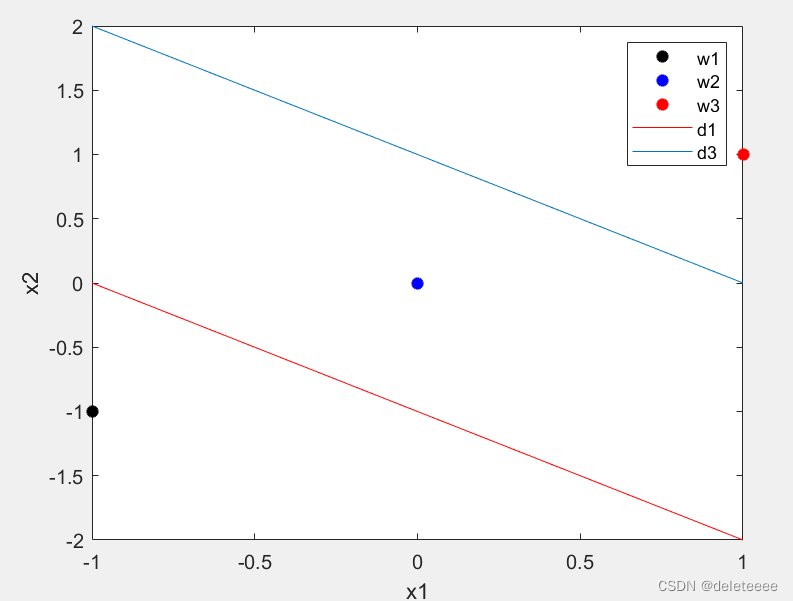
圖4分類結果及判別函數

可以看出訓練樣本可以被清晰的分成三類。

3. 結果與分析

3.1 兩類樣本

兩類樣本的感知器實驗中，對于訓練樣本進行增廣和將w2樣本乘以（-1）的處理可以讓我們在判斷分類結果時只需要判斷結果是否大于0即可，使得程序也可以更加簡便，最終的分類結果可以通過三維圖像來清晰的表示

3.2 三類樣本

三類樣本分類在訓練數據的處理過程中不能做乘以（-1）的處理，在迭代過程中需要對每一類的訓練數據計算所有的判別函數值并進行比較。

從實驗過程中也可以看出感知器算法就是一種賞罰過程，分類錯誤則修改權向量，使其向正確方向轉化，分類正確則不變。