常用算法思想及模板

今天繼續整理一些關于算法競賽中C++適用的一些模板以及思想。

保留x位小數

保留x位小數在C語言中可以使用printf中的"%.xf"來實現，但是很多C++選手由于關閉了同步流，害怕cin、cout與scanf、printf混用容易出錯，所以就給大家介紹一個強制保留x位小數的代碼格式。

cout<<fixed<<setprecision(x)<<（浮點型變量）;

其中的x可以根據題目中的要求更改，接下來看一道例題來對這個函數加深印象。

排隊接水

題目鏈接：排隊接水

排隊接水問題是一個非常典型的貪心問題，其中貪心的過程就不過多贅述了，原則就是前面的人消耗的時間越多，后面所有人等待的時間就越多，所以要讓耗時小的人在前面，這樣來構成全局最優解。可以試想一下，同樣是兩個人，其中一個人需要1小時，另一個人需要10分鐘，如果讓耗時多的人先接水的話，總時間就是這個人的耗時 + 后面的人等待其接水的耗時 + 后面的人的耗時，所以要對耗時進行排序，根據貪心原則讓耗時少的人先接水。

// Problem: P1223 排隊接水
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1223
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;void solve()
{int n;cin>>n;vector<pii> a(n+1);for(int i=1;i<=n;i++){cin>>a[i].fi;a[i].se = i;}sort(a.begin()+1,a.end());//貪心double sum = 0,ans=0;for(int i=1;i<=n;i++){cout<<a[i].se<<' ';if(i==n) break;//因為求的是等待時間 最后一個人不算sum += a[i].fi;ans += sum;}cout<<endl;//保留2位小數!cout<<fixed<<setprecision(2)<<ans/n;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

最長上升子序列

最長上升子序列是dp的一類入門題目，我在前面的博客中有做過對一些常見的線性DP的題型、用法以及模板內容的介紹，對這一塊不熟悉的小伙伴可以去看一下：線性DP，對于最長上升子序列，如果求的是長度，可以用遍歷 + 二分的方式降低時間復雜度，而如果是需要求出具體的以每一個元素結尾的長度的話就需要用到雙重循環來解決了（當然也可以用時間復雜度更低的單調隊列來解決，單調隊列我也有過總結，感興趣的小伙伴也可以去看一下總結的模板：入門，推廣?具體情況視題目而定），接下來看一道相關的題目。

合唱隊形

這道題用到了正向和逆向雙向相結合的思路，這種思想特別重要！很多像單調棧、最長子段和之類的題目也會用到這樣的思想，對于這道題而言我們需要正向用一遍最長上升子序列求出以每個點結尾的最長上升子序列的長度，然后逆向再跑一遍求出以每個元素開頭的最長下降子序列的長度，然后再遍歷一遍每個元素求出最大值，就是一共可以留下來的人數，題目中要求的移除的人數只需用總人數減去留下的人數即可得出。

// Problem: P1091 [NOIP 2004 提高組] 合唱隊形
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1091
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;void solve()
{int n;cin>>n;vector<int> a(n+1);for(int i=1;i<=n;i++) cin>>a[i];int l[n+1],r[n+1];// for(int i=1;i<=n;i++) l[i] = 1,r[i] = 1;fill(l+1,l+1+n,1);fill(r+1,r+1+n,1);for(int i=2;i<=n;i++)//正序最長上升子序列{for(int j=1;j<i;j++)if(a[j] < a[i]) l[i] = max(l[i],l[j] + 1);}for(int i=n-1;i>=1;i--)//逆序最長上升子序列（正序最長下降子序列）{for(int j=n;j>i;j--)if(a[j] < a[i]) r[i] = max(r[i],r[j] + 1);}int mx = -inf;for(int i=1;i<=n;i++){mx = max(mx,r[i] + l[i] - 1);//減去重復計算的自己}cout<<n - mx<<endl;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

歸并排序

相信部分C++選手對排序并不感興趣，因為STL中有自帶的搞笑的sort排序，在nlogn的時間復雜度下滿足了很多場景的需要，但是，歸并排序的時間復雜度也是nlogn，而且有很多題型都用到了類似于歸并排序中的分治思想，即將大問題轉化為很多個小問題，然后通過對小問題的高效解決來使得總問題的解決的思想，其中較為典型的就是逆序對問題，這個問題就是在歸并排序的合并過程中完成的！下面來回顧一下歸并排序的代碼以及對逆序對這一問題的高效求解。

逆序對

題目鏈接：逆序對

我們對逆序對的尋找不需要每次都遍歷計數，而是可以先將集合分為兩個部分，而這兩個部分又是有序的兩個集合，我們可以對兩個集合的元素進行比較大小的同時用O(1)的方法計算逆序對的數量，在合并的過程中如果左邊的集合中的元素小，直接將左邊這個元素合并上去，反之如果左邊的元素大，就應該將右邊的元素合并上去，而此時左邊剩余元素的數量就是以右邊的這個較小的數位第二個數的逆序對的數量，所以能在歸并排序合并過程的同時就將逆序對的數量進行統計了。代碼如下所示：

// Problem: P1908 逆序對
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1908
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 5e5+10;
vector<int> a(N,0),b(N,0);
int res=0;
void gb_sort(int l,int r)
{if(l >= r) return ;int mid = (l + r) >> 1;gb_sort(l,mid);gb_sort(mid+1,r);//分治過程int i=l,j=mid+1,k=l;//分治過程while(i <=mid && j <= r)//歸并過程{if(a[i] <= a[j]) b[k++] = a[i++];else b[k++] = a[j++],res += mid - i + 1;}while(i <= mid) b[k++] = a[i++];//對剩余元素的處理while(j <= r) b[k++] = a[j++];//對剩余元素的處理for(int i=l;i<=r;i++) a[i] = b[i];//將排序后的數組保存
}
void solve()
{int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];gb_sort(1,n);// for(int i=1;i<=n;i++) cout<<a[i]<<' ';cout<<res<<endl;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

高精度運算

C/C++選手的痛！在藍橋杯等一些賽事中經常出現，高精度和低精度之間的混合運算比較簡單，正常模擬即可，我也有過總結，需要的小伙伴可以去主頁拿。這里主要整理高精度乘高精度下的快速冪。

麥森數

題目鏈接：麥森數

這道題的數據范圍比較大，不僅僅用到了高精度??高精度，還需要用快速冪來優化，因為是2的n次方所以就要想到了以2位初始值的快速冪，又因為數太大了（光看樣例就已經很恐怖了）所以就又想到了高精度，這時候整體的代碼思路就出來了，實現起來也不難，整理這道題的主要原因就是便于對之后的快速冪以及高精度算法模板的需要，有需要的小伙伴也可以保存起來以后備用。

// Problem: P1045 [NOIP 2003 普及組] 麥森數
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1045
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 505;
vector<int> a(N,0),res(N,0);
void gjc_begin()
{int t=0,c=0;vector<int> temp(1010,0);for(int i=1;i<=500;i++){for(int j=1;j<=500;j++) temp[i+j-1] += a[i] * a[j];}for(int i=1;i<=500;i++){temp[i] += t;a[i] = temp[i] % 10;t = temp[i] / 10;}
}
void gjc_end()
{int t=0,c=0;vector<int> temp(1010,0);for(int i=1;i<=500;i++){for(int j=1;j<=500;j++) temp[i+j-1] += res[i] * a[j];}for(int i=1;i<=500;i++){temp[i] += t;res[i] = temp[i] % 10;t = temp[i] / 10;}
}
void ksm_plus(int x)
{while(x){if(x&1) gjc_end();gjc_begin();x >>= 1;}
}
void solve()
{int n;cin>>n;a[1] = 2,res[1] = 1;//快速冪的初始值位2 因為要求的是2的次方ksm_plus(n);int num=0;//數學公式直接計算2^n的位數cout<<(int)(n*log10(2) + 1)<<endl;int cnt=0;int t = 1;while(res[t] == 0)//對最后的 -1 操作進行計算{res[t] = 9;t++;}res[t]--;for(int i=500;i>0;i--){cout<<res[i];cnt++;if(cnt == 50){cout<<endl;cnt = 0;}}
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

求位數的高效方法

求x的位數相信很很堵人都會了，用 (int)log10(x) + 1即可，也可轉為字符串求長度。

這道題還需要用到的數學知識就是2的n次方的位數，如果用模擬法計算的話還需要用到高精度算法，而如果使用數學方法的話就很方便了，而且時間復雜度也不高，具體實現公式為：

(int)(n*log10(2) + 1)

倍增法

倍增法也是一個常用的算法，其中在求最近共同祖先的時候最為有用，可以將每次的O(N)時間復雜度的查詢壓縮至單次O(logN)的時間復雜度，適用于多次查詢最近共同祖先(LCA)的情況，具體思路如下：其中數組f[n][m]表示n的第2^m級祖先， 最重要的是在dfs求深度時對倍增ST表進行預處理

?圖中左側位預處理階段，右側為查詢LCA階段。

LCA最近共同祖先

題目鏈接：LCA最近共同祖先【模板】

為了方便之后對這一塊模板代碼的內容進行整理，所以我在這里用一個模版題來對倍增法求LCA做一個記錄，如果之后有需要的話可以參考這個模板。

// Problem: P3379 【模板】最近公共祖先（LCA）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3379
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 500010;
int n,m,s;
vector<int> a[N];
int dep[N],fu[N][30];
void dfs(int x,int fa)//深搜預處理階段
{dep[x] = dep[fa] + 1;fu[x][0] = fa;for(int i=1;i<30;i++) fu[x][i] = fu[fu[x][i-1]][i-1];//祖先預處理階段for(auto i : a[x]){if(i == fa) continue;//無向邊所以都存，防止重復訪問父節點dfs(i,x);}
}
int LCA(int x,int y)
{if(dep[x] < dep[y]) swap(x,y);while(dep[x] > dep[y]) x = fu[x][(int)log2(dep[x] - dep[y])];//先移動到同一層if(x == y) return x;//移動到同一層就重合了說明這個就是祖先了for(int i=log2(dep[x]);i>=0;i--)//根據二進制（2的冪次方）分解找到LCA的下一層（子節點）{if(fu[x][i] != fu[y][i])是共同祖先但是要保證是最近的所以在沒找到時才更新{x = fu[x][i];y = fu[y][i];}}return fu[x][0];//這一層的上一層就是LCA
}
void solve()
{cin>>n>>m>>s;for(int i=1;i<n;i++){int u,v; cin>>u>>v;a[u].push_back(v);a[v].push_back(u);}dfs(s,0);while(m--){int x,y;cin>>x>>y;cout<<LCA(x,y)<<endl;}
//	cout<<fixed<<setprecision(x)<< ; 
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

[eJOI 2020] Fountain (Day1)?

題目鏈接：[eJOI 2020] Fountain (Day1)

這道題是很好的一道題，他不僅僅考察了對倍增的運用，而且還考察了單調棧。廢話不多說，接下來就來看一下這道題的詳細解析。

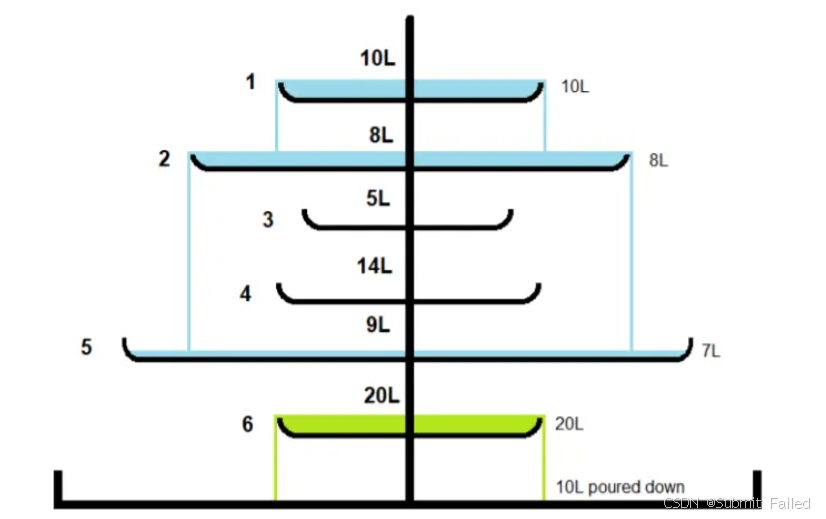
首先看到這到題第一反應就是從這個位置開始一直找后面的比當前元素要大的位置，然后不斷的更新value，最后到哪一個地方value小于或等于這里的盤子了就說明找到最終的答案了但是每次都遍歷所有的點就會超時，那么我們就開始想怎么去優化，我們首先可以想到用單調棧來記錄每一個元素下邊的第一個大于他的元素（等于不行!）這樣就不用每次都從當前點來事遍歷找第一個大于他的點了，只需要O(n)的復雜度就能處理完這一操作，但是這就完了嗎，交上去發現只有30分，還能怎么優化呢？我們想既然有了單調性的話，能不能用二分，可是二分還需要知道每一段的容量，也不好求，我們既然是從當前開始一直找到下一個大于當前的點，那我們是否可以跳著找呢，跳著找第2的冪次方個大于他的盤子，用倍增ST表來解決呢？靈感來源于：

所以我們可以先用單調棧（因為是右邊第一個大于他的元素，所以用逆序遍歷的單調遞減棧來實現，對單調棧這一方面不熟悉的小伙伴可以去看我的單調棧知識點的總結：單調棧詳解）來處理每一段單調遞增的盤子，然后將他們建樹，這樣就可以用倍增法來實現跳著找了。

將🌳建起來大概是這樣，相信大家能夠更形象地理解：

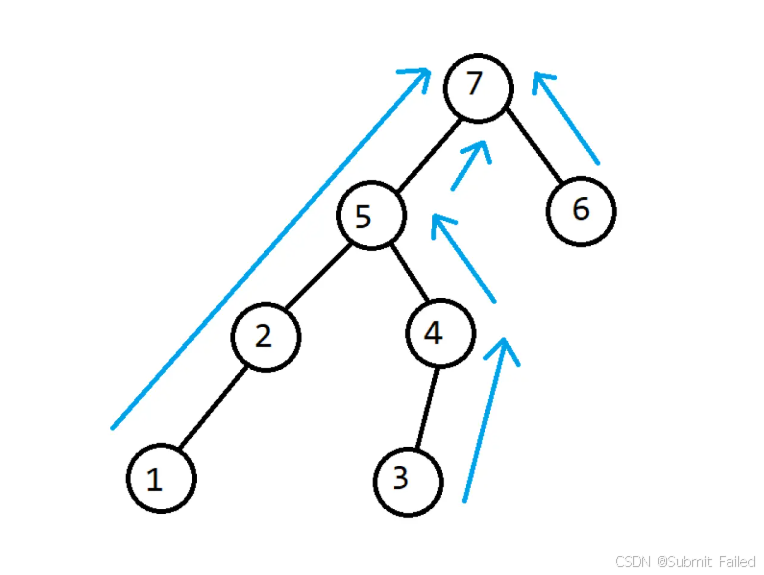
代碼如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first  
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;  // 無窮大
const int N = 1e5 + 10;
// 定義各數組和變量
vector<int> a(N,0),v(N,0),r(N,0);  // a存儲直徑，v存儲容量，r存儲右側第一個大于當前直徑的噴泉編號
stack<int> st;       // 單調棧
int n,m;             // n個噴泉，m次查詢
vector<int> e[N];    // 鄰接表存儲樹結構
vector<int> dep(N,0); // 存儲每個節點的深度
int fu[N][30],g[N][30]; // fu[i][j]表示i節點向上2^j層的祖先，g[i][j]表示i節點向上2^j層的容量和// DFS預處理倍增數組
void dfs(int x,int fa)
{dep[x] = dep[fa] + 1;  // 計算當前節點深度fu[x][0] = fa,g[x][0] = v[fa];  // 初始化直接父節點和容量// 預處理倍增數組for(int i=1;i<30;i++) {fu[x][i] = fu[fu[x][i-1]][i-1];// 計算祖先g[x][i] = g[fu[x][i-1]][i-1] + g[x][i-1];// 計算容量和}// 遞歸處理子節點for(auto i : e[x]) dfs(i,x);
}
void solve()
{cin>>n>>m;// 設置哨兵節點a[n+1] = inf,v[n+1] = inf;  // 第n+1個噴泉作為邊界// 輸入每個噴泉的直徑和容量for(int i=1;i<=n;i++) cin >> a[i] >> v[i];// 單調棧處理，找到每個噴泉右側第一個直徑大于它的噴泉for(int i=n;i>=1;i--){// 維護單調遞減棧while(!st.empty() && a[st.top()] <= a[i]) st.pop();// 如果棧空則指向哨兵，否則指向棧頂r[i] = (st.empty() ? n+1 : st.top());st.push(i);  // 當前噴泉入棧} // 構建樹結構for(int i=n;i>=1;i--) e[r[i]].push_back(i);// 從哨兵節點開始DFS預處理dfs(n+1,0);// 處理查詢for(int i=1;i<=m;i++){int index,value; cin>>index>>value;// 如果當前噴泉容量足夠if(v[index] >= value){cout<<index<<endl;continue;}// 否則減去當前噴泉的容量value -= v[index];int x=index;int ans=0;// 倍增查找能容納剩余水量的最低祖先for(int i=25;i>=0;i--){if(g[x][i] <= value && (1LL<<i) <= dep[x]){value -= g[x][i];x = fu[x][i];}if(value == 0) ans = x;}// 如果還有剩余水量，再向上走一步if(ans == 0) ans = fu[x][0];// 輸出結果，如果是哨兵則輸出0if(ans == n+1) cout<<0<<endl;else cout<<ans<<endl;}
}signed main()
{IOS  // 加速輸入輸出int T=1;while(T--) solve(); return 0;
}

之后的算法思維以及解題方法總結都會在本文進行更新，有興趣對這一塊內容進行整理的小伙伴可以保存起來。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/916967.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/916967.shtml
英文地址，請注明出處：http://en.pswp.cn/news/916967.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

GitLab 倉庫 — 常用的 git 命令

GitLab 倉庫 — 常用的 git 命令

在公司的 gitlab 公共倉庫中寫代碼做項目時&#xff0c;主要涉及以下常用 git 命令&#xff1a;一、單個命令講解1. 拉取代碼&#xff08;1&#xff09;git clone [倉庫 URL]?克隆遠程倉庫到本地&#xff08;需確保 URL 正確&#xff09; ?&#xff08;?2&#xff09;git pu…
閱讀更多...
【28】C# WinForm入門到精通 ——多文檔窗體MDI【屬性、方法、實例、源碼】【多窗口重疊、水平平鋪、垂直平鋪、窗體傳值】

【28】C# WinForm入門到精通 ——多文檔窗體MDI【屬性、方法、實例、源碼】【多窗口重疊、水平平鋪、垂直平鋪、窗體傳值】

文章目錄1多文檔窗體MDI2 基本設置3 實例&#xff1a;多窗口重疊、水平平鋪、垂直平鋪3.1 主窗口屬性設置3.2 主窗口3.3 主窗口窗口添加MenuStrip菜單3.4 添加處理函數3.5 測試效果4 利用窗體參數定義進行傳值4.1 在Form2、Form3添加相關控件4.2 Form3 定義函數public Form3(st…
閱讀更多...
【計算機科學與應用】基于Session欺騙攻擊的Web應用程序防護

【計算機科學與應用】基于Session欺騙攻擊的Web應用程序防護

導讀&#xff1a; 本文對Web應用程序開發中的Session欺騙攻擊進行了闡述&#xff0c;詳細講解了防范Session欺騙攻擊的三種傳統方法&#xff0c;并給出了防范代碼&#xff0c;分析了三種傳統防范方法的不足&#xff0c;新設計了一種通過Referer信息驗證來加強對Session欺騙的防…
閱讀更多...
yolo8+阿里千問圖片理解（華為簡易版小藝看世界）

yolo8+阿里千問圖片理解（華為簡易版小藝看世界）

? 實現目標 按下空格鍵 → 獲取攝像頭當前畫面&#xff1b; 將圖片上傳給 大模型 接口&#xff0c;讓其“看圖說話”&#xff1b; 獲取返回描述后&#xff0c;以字幕形式展示在圖像畫面上&#xff1b; 持續顯示識別結果&#xff0c;直到下次按空格。 &#x1f9e0; 需要準…
閱讀更多...
【ee類保研面試】數學類---線性代數

【ee類保研面試】數學類---線性代數

25保研er&#xff0c;希望將自己的面試復習分享出來&#xff0c;供大家參考 part0—英語類 part1—通信類 part2—信號類 part3—高數類 part100—self項目準備 文章目錄線性代數知識點大全**1. 余子式與代數余子式****2. 行列式的含義****3. 矩陣的秩&#xff08;Rank&#xf…
閱讀更多...
在 Scintilla 中為 Squirrel 語言設置語法解析器的方法

在 Scintilla 中為 Squirrel 語言設置語法解析器的方法

Scintilla 作為一個強大的開源文本編輯控件&#xff0c;通過配置語法解析器&#xff0c;能夠對多種編程語言實現語法高亮、代碼折疊等實用功能。若要為新語言 Squirrel 設置語法解析器&#xff0c;可參考以下步驟&#xff1a;?創建 Lexer 源文件&#xff1a;Scintilla 通過 Le…
閱讀更多...
Go語言核心知識點補充

Go語言核心知識點補充

Go語言核心知識點補充 make函數、for循環與輸入處理詳解 在前幾章的內容中&#xff0c;我們介紹了Go語言的基礎語法、變量聲明、切片、循環等核心概念。但在實際開發中&#xff0c;一些細節性的知識點往往決定了代碼的健壯性與效率。 本文將針對前幾章涉及到的變量聲明與初始化…
閱讀更多...
AI服務器中，EEPROM有哪些部件使用，需要存儲哪些信息？

AI服務器中，EEPROM有哪些部件使用，需要存儲哪些信息？

在AI服務器中&#xff0c;EEPROM&#xff08;電可擦可編程只讀存儲器&#xff09;主要用于存儲關鍵組件的配置數據、身份信息和校準參數。以下是主要組件及其存儲內容&#xff1a; 一、核心組件及存儲數據主板&#xff08;Baseboard Management Controller, BMC&#xff09; FR…
閱讀更多...
It學習資源下載

It學習資源下載

一.UI 8個高質量UI設計網站&#xff0c;靈感收集必備&#xff01;
閱讀更多...
Docker Compose ：從入門到企業級部署

Docker Compose ：從入門到企業級部署

Docker Compose &#xff1a;從入門到企業級部署1. Docker Compose 核心概念1.1 Compose 架構全景圖2. 完整開發工作流2.1 典型開發流程2.2 多服務示例項目結構3. 核心配置詳解3.1 服務配置矩陣3.2 網絡拓撲示例4. 企業級部署方案4.1 多環境配置管理4.2 擴展部署架構5. 高級技巧…
閱讀更多...
1.2.vue插值表達式

1.2.vue插值表達式

在 Vue.js 中&#xff0c;插值表達式是用于在模板中顯示數據的一種方式。它使用雙大括號語法 {{ }} 來包裹需要輸出的變量或表達式的值。Vue 會自動將這些表達式的值插入到 HTML 文檔中相應的位置。插值表達式基本用法最基本的插值表達式形式就是直接在模板中引用 Vue 實例中的…
閱讀更多...
Python數據處理基礎（學習筆記分享）

Python數據處理基礎（學習筆記分享）

Python數據處理入門 常用庫學習 numpy NumPy&#xff08;Numerical Python&#xff09; 是 Python 中用于高效數值計算的庫&#xff0c;核心是提供一個強大的 ndarray?&#xff08;多維數組&#xff09;對象&#xff0c;類似于 C/C 中的數組&#xff0c;但支持更豐富的操作&a…
閱讀更多...
力扣面試150題--顛倒二進制位

力扣面試150題--顛倒二進制位

Day 89 題目描述思路 二進制的算法&#xff0c;將十進制轉化為二進制&#xff0c;有一點需要注意&#xff0c;直接采取庫函數轉化為二進制再反轉會出現問題&#xff08;這也是為什么我要補0的原因&#xff09;&#xff0c;因為轉化過去不滿足32位的二進制&#xff0c;前面不會當…
閱讀更多...
【ResNet50圖像分類部署至RK3588】模型訓練→轉換RKNN→開發板部署

【ResNet50圖像分類部署至RK3588】模型訓練→轉換RKNN→開發板部署

已在GitHub開源與本博客同步的ResNet50v2_RK3588_Classificationt項目&#xff0c;地址&#xff1a;https://github.com/A7bert777/ResNet50v2_RK3588_Classification 詳細使用教程&#xff0c;可參考README.md或參考本博客第八章 模型部署 文章目錄一、項目回顧二、模型選擇介…
閱讀更多...
C# _泛型

C# _泛型

目錄 泛型是什么? 泛型的主要優勢 創建一個泛型類 泛型方法 泛型是什么? 泛型是通過參數化來實現同一份代碼上操作多種數據類型 利用參數類型將參數的類型抽象化 從而實現靈活的復用 總結: 通過泛型可以實現在同一份代碼上操作多種數據類型的邏輯 將類和類中的成員定義…
閱讀更多...
Vue路由鉤子完全指南

Vue路由鉤子完全指南

Vue.js中的路由導航鉤子&#xff08;Navigation Guards&#xff09;主要用于在路由導航過程中進行攔截和處理&#xff0c;確保訪問控制和狀態管理。以下是主要分類及使用方法&#xff1a; 1. 全局鉤子函數 作用于整個路由實例&#xff0c;需在路由配置外定義&#xff1a; befor…
閱讀更多...
RAGFlow 登錄界面點擊登錄無反應，控制臺報錯 502 Bad Gateway 解決方法

RAGFlow 登錄界面點擊登錄無反應，控制臺報錯 502 Bad Gateway 解決方法

遇到的問題 在使用RAGFlow的時候&#xff0c;登錄不進去&#xff0c;但是之前能登錄。 還出現了輸入地址直接進入工作界面&#xff0c;但是進行不了任何操作的bug&#xff1b;以及無法上傳文檔的問題&#xff08;其實都是因為沒登錄&#xff09;。 登陸界面報錯如圖顯示。 …
閱讀更多...
數據結構第3問：什么是線性表？

數據結構第3問：什么是線性表？

線性表 線性表由具有相同數據類型的n個元素構成&#xff0c;這些元素之間存在一一對應的線性關系。其中n為表長&#xff0c;當n0的時候線性表是一個空表。簡單來說&#xff0c;線性表中的元素排列成一條線&#xff0c;每個元素最多有一個直接的前驅和后繼&#xff08;除第一個和…
閱讀更多...
常見CMS 靶場復現

常見CMS 靶場復現

一、wordpass1.修改模版文件getshell搭建網站登錄網站后臺更改網站模版的相關文件寫入一句話木馬憑借路徑訪問/wp-content/themes/twentyfifteen/404.php/?aphpinfo();2.上傳夾帶木馬的主題getshell外觀-->主題-->添加-->上傳-->瀏覽-->安裝-->訪問木馬文件…
閱讀更多...
Elasticsearch - 倒排索引原理和簡易實現

Elasticsearch - 倒排索引原理和簡易實現

倒排索引的功能設計倒排索引&#xff08;Inverted Index&#xff09;是一種高效的數據結構&#xff0c;常用于全文搜索和信息檢索系統。它的核心思想是將文檔中每個關鍵字&#xff08;term&#xff09;與包含該關鍵字的文檔列表進行映射。以下是實現倒排索引功能的設計步驟和代…
閱讀更多...
最新文章

Copyright @ 2022~2023