簡單介紹跳表

? 跳表（Skip List）是一種可以進行對數級別查找的數據結構，它通過在數據中構建多級索引來提高查詢效率。跳表是一種基于鏈表的隨機化數據結構，其本質是由多個鏈表組成，每個鏈表中的元素都是原始鏈表中的元素。

? 我們知道鏈表的查找時間復雜度是O（N），如果這個鏈表數據是有序的，還是O（N），我們如何利用有序這一點，來進行優化呢？接下來就是我們的主角跳表登場。

? 跳表在實際應用中有許多用途，例如作為Redis等數據庫的有序數據結構實現，以及作為平衡樹等數據結構的替代方案。與其他數據結構相比，跳表具有實現簡單、空間復雜度低、查詢效率高等優點。

?

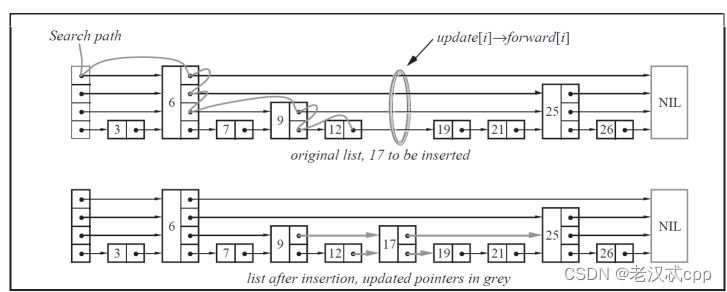
注意重點，在這種處理下，我們插入的結點的層數是隨機的！如此一來，插入刪除操作就簡化了很多。

skiplist的效率?

? 首先要分析，這個隨機層數是怎么來的。一般跳表會設置一個最大的層數限制maxLevel。其次會設計一個概率p。這個p就是指 最開始從第一層開始，每多一層的概率為p。

? 最大層數限制很好理解，這個p就是每次插入的時候，由它來決定這個結點有多少層。每多一層其實就是多一個指針。

在Redis中，這兩個參數的取值為

p = 1/4
maxLevel = 32

?

再簡單分析這個p就是：

平均計算如下：

?

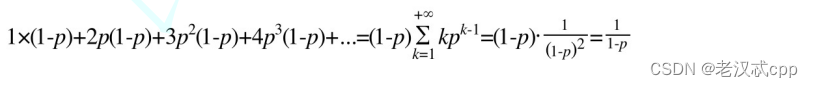?skiplist的簡單實現

? 其實skiplist只要理解了思想，實現起來還是比較簡單了，我們可以參考力扣上的一道題

1206. 設計跳表 - 力扣（LeetCode）?

?代碼：

#pragma once#include <iostream>
#include <vector>
#include <time.h>
#include <random>
#include <chrono>using namespace std;struct SkiplistNode
{int _val;vector<SkiplistNode*> _nextV;  // 層數也就是指針，用數組存起來SkiplistNode(int val, int level):_val(val), _nextV(level, nullptr){}
};class Skiplist
{typedef SkiplistNode Node;
public:Skiplist(){srand(time(0));// 頭結點的層數設置為1_head = new SkiplistNode(-1, 1);}bool search(int target){Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){// 目標值比下一個結點的值要大的話，就往右走// 如果下一個結點是空（尾），或者目標值比下一個結點要小，就向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < target){// 往右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target){// 往下走--level;}else{// 找到了return true;}}return false;}vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;// 記錄 被改動的位置的每一層的前一個結點指針vector<Node*> prevV(level + 1, _head);while (level >= 0){// 同理 比下一個結點大就往右走// 下一個結點是空，或者目標值比下一個結點要小，就往下走if (cur->_nextV[level] && cur->_nextV[level]->_val < num){cur = cur->_nextV[level]; // 向右走}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num) {// 注意 這里num等于也是要進來的// 更新level層的前一個prevV[level] = cur;--level; // 向下走}}return prevV;}void add(int num){vector<Node*> prevV = FindPrevNode(num);int n = RandomLevel();Node* newnode = new Node(num, n);// 注意：如果n超過了當前的最大層，那么就要相應的提高_head的層數if (n > _head->_nextV.size()){_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}// 鏈接前后結點for (size_t i = 0; i < n; ++i){// 注意順序，先設置好目標結點的指針指向newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}}bool erase(int num){vector<Node*> prevV = FindPrevNode(num);// 如果第一層的下一個不是val，則val不在表中if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num){return false;}else{Node* del = prevV[0]->_nextV[0];// 先將del結點的前后結點鏈接起來for (size_t i = 0; i < del->_nextV.size(); ++i){prevV[i]->_nextV[i] = del->_nextV[i];}delete del;// 如果刪除的這個結點改變了跳表結點的當前最高層數，// 那么應該將頭結點的層數降到第二高的層數int i = _head->_nextV.size() - 1;while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;}return false;}int RandomLevel(){size_t level = 1;// rand() 的取值范圍在 [0,RAND_MAX] 之間// 這里就轉換成了 如果區間在 [0,_p]就加一層while (rand() <= RAND_MAX * _p && level < _maxLevel){++level;}return level;}
private:Node* _head;size_t _maxLevel = 32;double _p = 0.25;
};void Test()
{Skiplist sl;//int a[] = { 5, 2, 3, 8, 9, 6, 5, 2, 3, 8, 9, 6, 5, 2, 3, 8, 9, 6 };int a[] = { 1, 2, 3, 4 };for (auto e : a){sl.add(e);}/*int x;cin >> x;sl.erase(x);*/sl.erase(1);//cout << sl.erase(0) << " " << sl.erase(1) << endl;
}

? 跳表稍復雜一點的地方就是插入和刪除了。因為我們還要需要找到目標結點的每一層的前一個結點，將它們放入數組中，然后才能處理好目標結點的前后結點之間的關系。

? 另外就是它的查找邏輯，設cur來遍歷結點，那么cur的移動就有兩種情況，一種是目標值大于cur下一個結點的值的話，cur就向右走；另一種就是小于，那么cur就向下走（--level）。再然后就是等于了。

跳表跟平衡搜索樹及哈希表的對比

跟平衡搜索樹?

? 二者都可以做到遍歷數據有序，并且時間復雜度都差不多。

? 跳表跟平衡搜索樹（AVL樹和RB樹）的優勢就是：

1. 跳表實現簡單，且容易控制。不像AVL樹和RB樹非常復雜，跳表這里我們刪除操作都很容易就實現了。

2.跳表的空間消耗相對較低，不像平衡搜索樹，不僅每個結點都有三叉鏈（指針），而且還要存平衡因子或者顏色。當跳表中的p = 1/2時，每個結點所包含的指針個數為2；p = 1/4時，每個結點所包含的指針個數為1.33。

因此，跟平衡搜索樹比起來，還有是有優勢的。

跟哈希表

跳表跟哈希表比起來，各有優缺點。

跳表的優點：

1.空間消耗還是略低哈希表。哈希表存在鏈表指針和表空間的消耗。

2.跳表遍歷數據能有序。

3.哈希表擴容時有性能損耗。跳表就沒有。

4.在極端場景下，哈希表哈希沖突高，效率下降的厲害，還需要紅黑樹來接力，增加了算法復雜度。

哈希表的優點：

時間復雜度是O（1），比跳表要快。

所以這樣看來，跳表跟哈希表比起來，有些還是有優勢的，但是沒有跟平衡搜索樹比起來那么大。