2867. 統計樹中的合法路徑數目
題目描述:
給你一棵?n?個節點的無向樹,節點編號為?1?到?n?。給你一個整數?n?和一個長度為?n - 1?的二維整數數組?edges?,其中?edges[i] = [ui, vi]?表示節點?ui?和?vi?在樹中有一條邊。
請你返回樹中的?合法路徑數目?。
如果在節點?a?到節點?b?之間?恰好有一個?節點的編號是質數,那么我們稱路徑?(a, b)?是?合法的?。
注意:
- 路徑?
(a, b)?指的是一條從節點?a?開始到節點?b?結束的一個節點序列,序列中的節點?互不相同?,且相鄰節點之間在樹上有一條邊。 - 路徑?
(a, b)?和路徑?(b, a)?視為?同一條?路徑,且只計入答案?一次?。
示例 1:
輸入:n = 5, edges = [[1,2],[1,3],[2,4],[2,5]] 輸出:4 解釋:恰好有一個質數編號的節點路徑有: - (1, 2) 因為路徑 1 到 2 只包含一個質數 2 。 - (1, 3) 因為路徑 1 到 3 只包含一個質數 3 。 - (1, 4) 因為路徑 1 到 4 只包含一個質數 2 。 - (2, 4) 因為路徑 2 到 4 只包含一個質數 2 。 只有 4 條合法路徑。示例 2:
輸入:n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]] 輸出:6 解釋:恰好有一個質數編號的節點路徑有: - (1, 2) 因為路徑 1 到 2 只包含一個質數 2 。 - (1, 3) 因為路徑 1 到 3 只包含一個質數 3 。 - (1, 4) 因為路徑 1 到 4 只包含一個質數 2 。 - (1, 6) 因為路徑 1 到 6 只包含一個質數 3 。 - (2, 4) 因為路徑 2 到 4 只包含一個質數 2 。 - (3, 6) 因為路徑 3 到 6 只包含一個質數 3 。 只有 6 條合法路徑。提示:
1 <= n <= 10^5edges.length == n - 1edges[i].length == 21 <= ui, vi <= n- 輸入保證?
edges?形成一棵合法的樹。
思路:
1)雖然他是想構成一棵樹,但個人覺得更像縮減版的圖,不過最后一句提示“輸入保證?edges?形成一棵合法的樹。”保證了樹的存在。但其實質相同,就是對圖的每一個節點,深度遍歷,然后統計“合法”的路徑數量
2)枚舉每個質數節點,從質數的鄰居開始dfs,統計在不經過質數的前提下能訪問到多少個非質數。以下圖為例,假設2的鄰居能訪問到3,4,5個非質數。
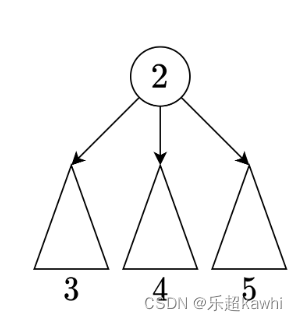
4和左邊這3個點,兩兩之間的路徑都只包含質數2。5和左邊這3+4個點,兩兩之間的路徑都只包含質數2.根據乘法原理,把4*3+5*7加到答案中。注:只考慮左邊是避免重復統計。最后,從2出發到下面這3+4+5=12個點的路徑也只包含質數2把12加到答案中。
代碼:
#標記10^5以內質數
MX=10**5+1
isPrime=[True]*MX
isPrime[1]=False
for i in range(2,isqrt(MX)+1):if isPrime[i]:for j in range(i*i,MX,i):#j為i的倍數,代表非質數isPrime[j]=Falseclass Solution:def countPaths(self, n: int, edges: List[List[int]]) -> int:#構建鄰接表g=[[] for _ in range(n+1)]for x,y in edges:g[x].append(y)g[y].append(x)def dfs(x:int,fa:int)->None:nodes.append(x)for y in g[x]:if y !=fa and not isPrime[y]:dfs(y,x)ans = 0size = [0] * (n + 1)for x in range(1, n + 1):if not isPrime[x]: # 跳過非質數continues=0for y in g[x]: # 質數 x 把這棵樹分成了若干個連通塊if isPrime[y]:continueif size[y]==0:#還沒計算的nodes=[]dfs(y,-1) # 遍歷 y 所在連通塊,在不經過質數的前提下,統計有多少個非質數for z in nodes:size[z]=len(nodes)# 這 size[y] 個非質數與之前遍歷到的 s 個非質數,兩兩之間的路徑只包含質數 xans+=size[y]*ss+=size[y]ans+=s #從x出發的路徑return ans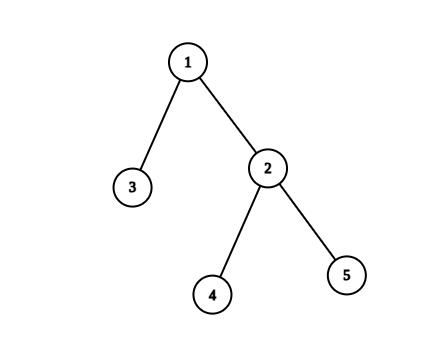







)





)
![[Java 探索者之路] 一個大廠都在用的分布式任務調度平臺](http://pic.xiahunao.cn/[Java 探索者之路] 一個大廠都在用的分布式任務調度平臺)





)