🚀 算法題 🚀

🌲 算法刷題專欄 | 面試必備算法 | 面試高頻算法 🍀
🌲 越難的東西,越要努力堅持，因為它具有很高的價值，算法就是這樣?
🌲 作者簡介：碩風和煒，CSDN-Java領域優質創作者🏆，保研|國家獎學金|高中學習JAVA|大學完善JAVA開發技術棧|面試刷題|面經八股文|經驗分享|好用的網站工具分享💎💎💎
🌲 恭喜你發現一枚寶藏博主,趕快收入囊中吧🌻
🌲 人生如棋，我愿為卒，行動雖慢，可誰曾見我后退一步？🎯🎯

🚀 算法題 🚀

🚩 題目鏈接

• 124. 二叉樹中的最大路徑和

? 題目描述

二叉樹中的 路徑 被定義為一條節點序列，序列中每對相鄰節點之間都存在一條邊。同一個節點在一條路徑序列中 至多出現一次 。該路徑 至少包含一個 節點，且不一定經過根節點。

路徑和 是路徑中各節點值的總和。

給你一個二叉樹的根節點 root ，返回其 最大路徑和 。

示例 1：

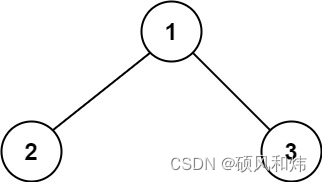
輸入：root = [1,2,3]
輸出：6
解釋：最優路徑是 2 -> 1 -> 3 ，路徑和為 2 + 1 + 3 = 6

示例 2：

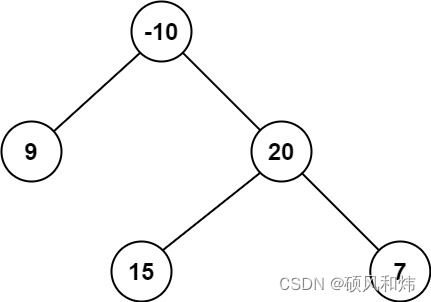
輸入：root = [-10,9,20,null,null,15,7]
輸出：42
解釋：最優路徑是 15 -> 20 -> 7 ，路徑和為 15 + 20 + 7 = 42

提示：

樹中節點數目范圍是 [1, 3 * 104]
-1000 <= Node.val <= 1000

🌟 求解思路&實現代碼&運行結果

---

? 二叉樹+遞歸

🥦 求解思路

1. 設計一個遞歸函數，用來獲取二叉樹的最大路徑和，同時，用一個max來與每次左右子樹遞歸的最大數值+當前根節點的數值比較，更新最大值。
2. 每次遞歸返回節點的最大貢獻值，可能是左子樹+當前節點，也可能是右子樹+當前節點，或者就是當前節點，最后不要忘了與0比較，只有大于0，才會取相應的節點。
3. 有了基本的思路，接下來我們就來通過代碼來實現一下遞歸的解法。

🥦 實現代碼

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private int max = Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {process(root);return max;}public int process(TreeNode root) {if (root == null)return 0;int leftSum = process(root.left);int rightSum = process(root.right);max = Math.max(max, leftSum + rightSum + root.val);return Math.max((Math.max(leftSum, rightSum) + root.val), Math.max(root.val, 0));}
}

🥦 運行結果

---

💬 共勉

最后，我想和大家分享一句一直激勵我的座右銘，希望可以與大家共勉！