1. 簡介

提出了紅杉優化算法（SequoiaOA），這是一種受紅杉森林生態系統自我調節動力學和彈性啟發的新型元啟發式方法，不同于傳統的奇異生物學或現象學靈感。開發一個全面的生態系統驅動框架，包括數學建模、系統分析和通過CEC基準測試和多約束工程問題進行驗證。當前的元啟發式算法通常局限于來自單一視角、孤立的生物行為或個體現象的靈感，導致了推動本研究的內在局限性。與傳統方法不同，本文從生態系統的角度探索復雜的生物系統，并進行全面的系統建模、分析和算法創新。具體而言，提出了一種受紅杉森林生態系統中觀察到的自我調節和恢復現象啟發的新型元啟發式優化算法，稱為紅杉優化算法（SequoiaOA）。紅杉生態系統表現出包括集體生長、資源共享和網絡、適應性和彈性、繁殖和多樣性以及精英保留在內的鮮明特征。基于這些現象，這項工作提出了SequoiaOA的第一個公式，從生態系統復雜性、自我調節和宏觀系統彈性的角度，通過算法建模和驗證來開發其數學模型和工程應用。

2.紅杉優化算法

紅杉的生態環境主要由這些非凡的巨人組成，也被稱為海岸紅杉，它們屬于柏樹科的紅杉屬。成熟的紅杉在溫暖、潮濕和陽光充足的環境中茁壯成長，可以達到70-120m的高度，壽命從800年到3000年不等，使它們成為世界上最非凡的自然奇觀之一。在這種生態環境中，紅杉表現出顯著的適應性和復原力。這一點可以從它們厚厚的樹皮和低樹脂含量以及海綿狀的吸水能力中得到證明，這賦予了它們對疾病和火災的高抵抗力。此外，紅杉表現出強大的生命力，其特點是快速生長和高成活率。即使被砍伐或損壞，紅杉也可以通過從毛刺中長出新樹來再生。紅杉樹的圖像可以從參考文獻[105]中獲得。
在紅杉的生態環境中，集體生長、資源共享和網絡的強烈存在。這一點的例證是這些樹木經常生長的密集集群，在保持土壤水分的同時提供相互保護以抵御強風和侵蝕。如果紅杉倒下或死亡，鄰近的樹木可以通過相互連接的根網絡支持新樹苗的生長，從倒下的“母親”樹的根部汲取水和養分。這種互利關系促進了個體的生存和群體的復原力[106]。紅杉的淺而廣泛的根系與周圍的植物和真菌形成共生網絡，促進了水和養分的共享交換。
在紅杉生態環境中，也非常強調繁殖和多樣性，以及精英保留。紅杉厚厚的樹皮和蓄水能力使它們能夠忍受火災，并通過再生迅速恢復。繁殖是通過種子傳播實現的，保持遺傳多樣性，并能夠適應不斷變化的環境條件。雖然火災可能會破壞一些植被，但它們也會促進種子萌發，維持紅杉生態系統的持續發展。紅杉優化算法的靈感來自紅杉樹的這些生長行為和彈性特征，其數學模型概述于以下部分。

2.1 初始化

與其他群體智能（SI）算法類似，紅杉優化算法（Sequoia OA）首先在解空間中初始化一組候選解。每個候選解代表一棵紅杉樹，如公式（1）所示：

$$X=[x_1,x_2,\dots ,x_D]\text{\hspace{1em}(1)}$$

其中$D$表示問題的維度。對于最小化問題，所有解如公式（2）所示，其中適應度值最小的紅杉樹解被視為當前迭代的最優解。若當前最優解的適應度值更小，則用其替換歷史最優解。

$$X_{pop}=\left[\begin{array}{ccccc}{x}_{1,1}& x_{1,2}& \dots & x_{1,D?1}& x_{1,D}\\ x_{2,1}& x_{2,2}& \dots & x_{2,D?1}& x_{2,D}\\ ?& ?& ?& ?& ?\\ x_{N?1,1}& x_{N?1,2}& \dots & x_{N?1,D?1}& x_{N?1,D}\\ x_{N,1}& x_{N,2}& \dots & x_{N,D?1}& x_{N,D}\end{array}\right]\text{\hspace{1em}(2)}$$

其中$X_{pop}$表示由紅杉樹群體組成的解，通過公式（3）初始化，而$1D$紅杉樹種群的完整位置，$N$表示紅杉樹種群的數目。

$$x_i=B+\text{rand}(B,1)\times (a?b)\text{\hspace{1em}(3)}$$

其中$x_i$表示個體$i$的位置或解向量，$a$和$b$表示優化問題的上下界，$\text{rand}(B,1)$生成一個0到1之間的隨機數，表示個體在上下界之間的隨機分布。

2.2 數學模型

2.2.1 集體生長資源共享與網絡

紅杉樹以集群方式生長，形成茂密的森林。其根系既淺又廣，與周圍的植物和真菌建立共生網絡，共享水分和養分。這種集體行為提供了抵御環境壓力的保護，根系網絡的資源共享使得群體內能夠合作與互助。受此群體行為啟發，算法設計可以增強地下資源共享機制作為一種協作調整策略。該策略通過群體中的個體向最優解靠攏，促進信息進一步共享，如公式（4）所示。通過計算群體中表現最優的一半個體的均值，引導整個群體向更優解靠近，模擬紅杉樹的資源共享機制。這種方式利用優秀個體的均值調整所有個體的解，通過促進整體優化過程實現有效的信息共享與合作。

$$x_i=n_i+\text{random}(0,1)\times ({\Sigma }_{top}?x_i)\text{\hspace{1em}(4)}$$

其中$n_i$表示個體$i$的位置或解向量，$\text{random}(0,1)$表示從正態分布生成一個隨機數，用于估計擾動${\Sigma }_{top}$表示群體中表現最優的一半個體的平均位置，總結了群體的集體知識。

2.2.2 適應性與韌性

紅杉樹以其卓越的適應性聞名。在干旱和火災等極端環境中，其厚實的樹皮和出色的儲水能力使其能夠抵御火災并迅速恢復。紅杉生長的生態系統常受火災事件影響。盡管火災可能對某些植被具有破壞性，但其清除了較弱的競爭者，將養分釋放到土壤中，并刺激紅杉種子的萌發。這一生長過程增強了森林的生物多樣性和韌性。受此自然過程啟發，如公式（5）所示，算法設計引入了隨機分布機制以模擬此類環境擾動。通過引入隨機擾動，算法能夠逃離局部最優并探索更廣闊的解空間，避免群體過早收斂。火災擾動機制是算法設計中的關鍵策略，增強了全局搜索能力和魯棒性。通過精確控制擾動概率，該方法確保擾動頻率既不會過高而影響收斂速度，也不會過低而陷入局部最優。

$$x_i=x_i+\text{random}(0,1)\times 0.5\text{if?}(\text{rand}<\text{fireProbability})\text{\hspace{1em}(5)}$$

其中$\text{fireProbability}(Fy)$表示火災擾動的概率，定義為$Fy=\max (0.5?0.5\times \frac{\text{iter}}{\text{maxIter}})$。概率隨迭代次數調整，并為群體中的每個個體分配隨機分布。$\text{random}(0,1)$用于從正態分布引入隨機擾動，模擬火災后的環境變化。$x_i$表示個體$i$的位置或解向量。$0.5$表示擾動幅度系數，控制擾動的強度。$\text{iter}$為當前迭代次數，$\text{maxIter}$為最大迭代次數，$\max (0,b)$表示取$a$和$b$的最大值，確保參數不低于特定閾值。

2.2.3 繁殖與多樣性

受紅杉樹通過種子傳播繁殖并維持遺傳多樣性以適應環境變化的啟發，算法采用交叉和變異機制。通過模擬生物繁殖中的基因重組和突變，這些機制引入多樣性并增強適應性，從而提高解的全面性。交叉使得有利特征得以傳遞和組合，而變異提供了新的探索方向，避免過早收斂。這種繁殖機制通過交替進行交叉和變異，使算法能夠以更多樣化的方式探索搜索空間，增加找到全局最優解的可能性。

(1) 交叉

交叉是指從兩個父代個體生成一個或多個后代的過程。交叉操作使得父代個體的特征得以重組和傳遞，使下一代能夠繼承父代的有利特征。交叉操作的過程增加了群體的多樣性，并有助于逃離局部最優。在算法設計中，如公式（6）和（7）所示，交叉操作通過兩個父代個體的線性組合實現：

$${\text{offspring}}_1=a\times x_i+(1?a)\times x_j\text{\hspace{1em}(6)}$$

$${\text{offspring}}_2=a\times x_{i+1}+(1?a)\times x_j\text{\hspace{1em}(7)}$$

其中$x_i$表示個體$i$的基因。${\text{offspring}}_1$和${\text{offspring}}_2$表示交叉后生成的兩個后代，$a$表示一個0到1之間隨機生成的權重系數，用于兩個個體基因的線性組合。通過隨機系數$a$實現交叉，并通過添加隨機擾動引入變異以增加解的多樣性。

(2) 變異

變異通過對個體進行隨機調整以引入新的遺傳特征。該操作增強了解的多樣性，防止群體收斂至局部最優。通過施加隨機擾動，算法能夠探索解空間的新區域，幫助逃離局部最優陷阱。變異操作如公式（8）所示：

$$\text{offspring}=\text{offspring}+\text{randn}(1,\text{dim})\times 0.3\text{if?}(\text{rand}<\text{mutationRate})\text{\hspace{1em}(8)}$$

其中$\text{mutationRate}(m_r)$表示變異發生的概率，定義為$m_r=\max (0.2?0.1\times \frac{\text{iter}}{\text{maxIter}},0.02)$。變異率決定每個后代是否進行變異。$\text{randn}(1,\text{dim})$表示生成一個與個體維度相同的向量，其每個元素為標準正態分布的隨機數。$\text{iter}$為當前迭代次數，$\text{maxIter}$為最大迭代次數。函數$\max (a,b)$返回$a$和$b$中的較大值，確保參數不低于特定閾值。

2.2.4 精英保留與最優解增強

受紅杉樹高大 stature 和長壽特性的啟發（使得最強個體能夠長期存活并繁殖），算法采用精英保留策略以保留最優解，確保最佳解在迭代過程中不被丟棄。同時，局部搜索機制模擬紅杉對微環境的精細適應，幫助發現更優解。局部搜索與精英保留機制共同模擬了自然選擇原則：局部搜索反映生物對微環境的適應，精英保留確保優良特征的傳遞。通過在每代中微調并保留最優解，這些機制提升了搜索過程的精度和穩定性。二者的結合實現了精細的局部探索與全局搜索的平衡，確保高質量解不被丟棄，從而提高算法的整體效率和魯棒性。

(1) 局部搜索機制

局部搜索機制通過對當前最優解施加微小擾動，模擬紅杉對局部環境的精細適應以發現更優解。具體數學表達式如公式（9）所示，其中對當前最優解施加小擾動生成新局部解，促進其鄰域內的局部搜索。

$$x_{\text{local}}=x_{\text{best}}+0.1\times \text{randn}(0,1)\text{\hspace{1em}(9)}$$

其中$x_{\text{local}}$表示局部搜索后的解，$x_{\text{best}}$表示當前最優解的位置，$\text{randn}(1,\text{dim})$表示生成維度為$\text{dim}$的隨機向量，其每個元素取自標準正態分布。

(2) 精英保留機制

精英保留機制通過保留精英個體至下一代，確保優良特征的繼承。具體操作如下：首先根據適應度值對所有個體排序，然后從排序后的群體中選擇前$\text{eliteSize}$個適應度值最高（最小化問題中為最低）的個體作為精英個體，最后用這些精英個體替換排序后前$\text{eliteSize}$個個體，使其進入下一代。此處$\text{eliteSize}$表示保留的精英個體數量。

2.2.5 SequoiaOA的流程圖與偽代碼

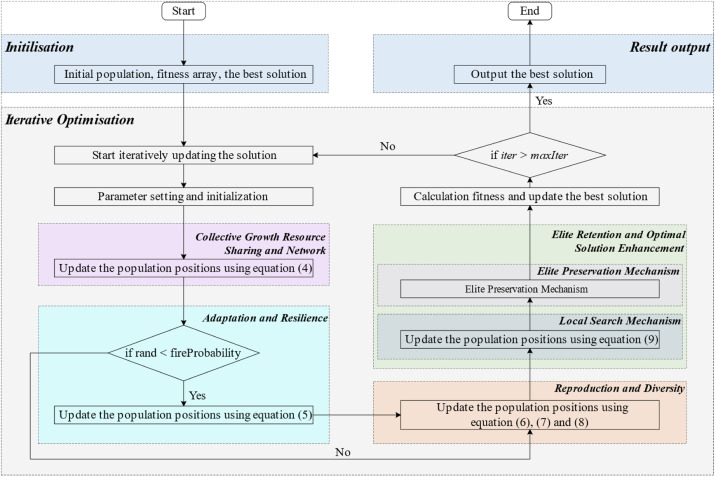
為清晰展示SequoiaOA的流程，圖1提供了算法流程圖，偽代碼如算法1所示。

% Sequoia Optimisation Algorithm(SequoiaOA)
% Developed in MATLAB R2022b
function [bestFitness, bestSolution, convergenceCurve] = SequoiaOA(popSize, maxIter, lb, ub, dim, fobj)% Initial populationpopulation = repmat(lb, popSize, 1) + rand(popSize, dim) .* (repmat(ub - lb, popSize, 1));% initializes the fitness arrayfitness = zeros(popSize, 1);for i = 1:popSizefitness(i) = fobj(population(i, :));end% initializes the best solution[bestFitness, bestIndex] = min(fitness);bestSolution = population(bestIndex, :);% convergence curveconvergenceCurve = zeros(1, maxIter);% Start iteratively updating the solutionfor iter = 1:maxIter% Dynamically adjust parametersfireProbability = max(0.3 - 0.15 * (iter / maxIter), 0.1);mutationRate = max(0.2 - 0.1 * (iter / maxIter), 0.02);% Sorted by fitness[sortedFitness, sortedIndices] = sort(fitness);sortedPopulation = population(sortedIndices, :);population = sortedPopulation;eliteSize = 2;eliteSolutions = population(sortedIndices(1:eliteSize), :);% Collective Growth Resource Sharing and NetworkhalfPopSize = round(popSize/2);topIndividuals = population(1:halfPopSize, :);meanTop = mean(topIndividuals, 1);population = population + randn(popSize, dim) .* (repmat(meanTop, popSize, 1) - population);% Adaptation and Resilienceif rand < fireProbabilitypopulation = population + randn(popSize, dim) * 0.5;end% Reproduction and Diversityfor i = 1:2:popSizeif i + 1 ≤ popSize% Crossoveralpha = rand;offspring1 = alpha * population(i, :) + (1 - alpha) * population(i + 1, :);offspring2 = alpha * population(i + 1, :) + (1 - alpha) * population(i, :);% Mutationif rand < mutationRateoffspring1 = offspring1 + randn(1, dim) * 0.3;offspring2 = offspring2 + randn(1, dim) * 0.3;end% Boundary Treatmentoffspring1 = max(min(offspring1, ub), lb);offspring2 = max(min(offspring2, ub), lb);% Regeneration Populationpopulation(i, :) = offspring1;population(i + 1, :) = offspring2;endend% Local Search MechanismlocalBest = bestSolution + 0.1 * randn(1, dim);localBest = max(min(localBest, ub), lb);localFitness = fobj(localBest);if localFitness < bestFitnessbestFitness = localFitness;bestSolution = localBest;end% Elite Preservation Mechanismpopulation(sortedIndices(end-eliteSize+1:end), :) = eliteSolutions;% Calculation fitnessfor i = 1:popSizefitness(i) = fobj(population(i, :));end% update the best solution[currentBestFitness, currentBestIndex] = min(fitness);if currentBestFitness < bestFitnessbestFitness = currentBestFitness;bestSolution = population(currentBestIndex, :);end% Records the convergence curveconvergenceCurve(iter) = bestFitness;disp(['Iteration=' num2str(iter) ', Best Fitness=' num2str(bestFitness)]);end
end

Shijie Fan, Ruichen Wang, Kang Su, Yang Song, Rui Wang, A sequoia-ecology-based metaheuristic optimisation algorithm for multi-constraint engineering design and UAV path planning,Results in Engineering,Volume 26,2025,105130, https://doi.org/10.1016/j.rineng.2025.105130.