定義

平衡二叉樹又稱為AVL樹，是具有以下性質的非空搜索樹：

1. 任一結點的左、右子樹均為AVL樹。
2. 根節點的左、右子樹高度差的絕對值不超過1.

對于二叉樹的任一結點T，其平衡因子（BF）定義為BF(T)= $h_L?h_R$，$h_L$和$h_R$分別是T的左、右子樹的高度。故AVL樹的平衡因子只能在{-1,0,1}中取值。

平衡樹的調整

當向一顆AVL樹插入新的結點時，該節點的平衡因子可能不在上述集合分為內。 這時需要做出”平衡化“處理，即相應的局部旋轉調整，時調整后的樹達到平衡。

單旋調整

右單旋（RR）

如圖，在第三個節點插入后，根節點mar的平衡因子為-2，樹不平衡。需要將樹做逆時針旋轉。
#
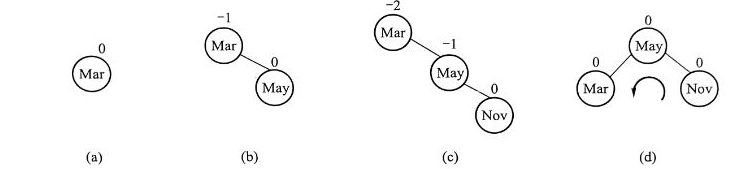
一般情況如下圖所示，在A的右節點B的右子樹里插入C，使得A的平衡因子變為-2，這時我們需要逆時針旋轉相關節點，把B至于A的位置，A置為B的子節點。若B有左子樹，將B的左子樹置為A的右子樹。

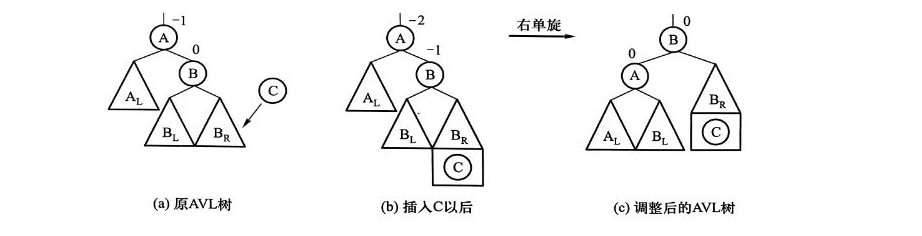
左單旋（LL）

一般情況下，在A節點的左節點B的左子樹下插入C節點后導致A節點不平衡，需要順時針旋轉相應節點，將B節點替代A節點位置，將A節點置為B的右節點，若B有右子樹，則將B的右子樹作為A的左節點。

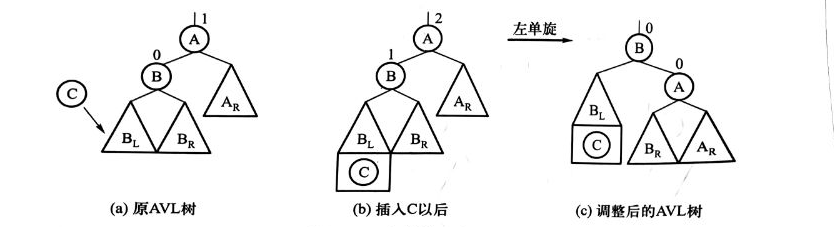
雙旋調整

LR型

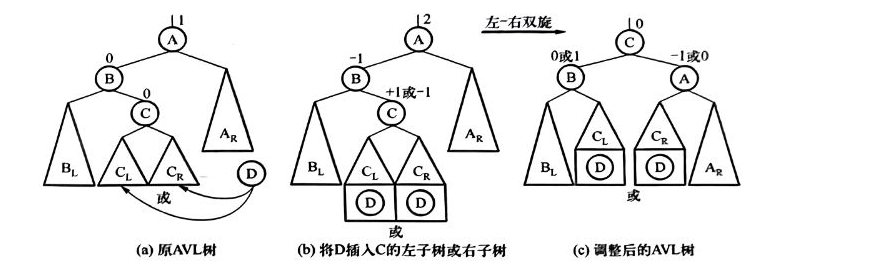
在A節點的左節點B的右子樹（以C為根節點）下插入D，稱為LR型不平衡。調整方式為將C至于A的位置，A及其右子樹調整為C的右子樹，C的左子樹作為B的右子樹，C的右子樹作為A的左子樹。

事實上，這一調整也可以視為對以B節點為根的子樹做一次右單旋，再對以A為根節點的子樹做一次左單旋。

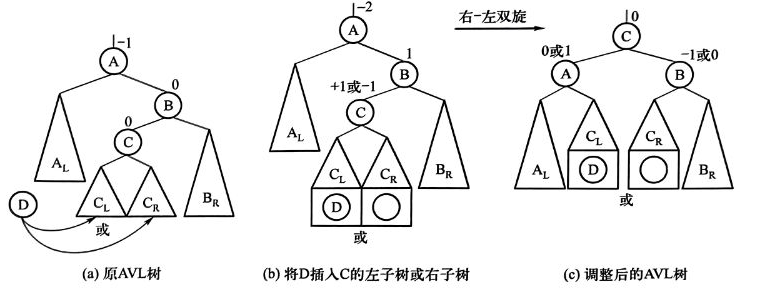
RL型

在A節點的右節點B的左子樹（以C為根節點）下插入D，稱為RL型不平衡。
調整方法為C替代A的位置，A以及A的左子樹作為C的左子樹，C的左子樹為A 的右子樹，C的右子樹作為B 的左子樹。

事實上，這一調整也可以視為對以B節點為根的子樹做一次左單旋，再對以A為根節點的子樹做一次右單旋。