LeetCode 78 子集

題目描述

給你一個整數數組?nums?，數組中的元素?互不相同?。返回該數組所有可能的子集（冪集）。

解集?不能?包含重復的子集。你可以按?任意順序?返回解集。

示例 1：

輸入：nums = [1,2,3]
輸出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

輸入：nums = [0]
輸出：[[],[0]]

思路

????????這道題目和普通的回溯問題的區別在于，每加入一次新的元素都要將結果加入result數組中，而不是需要判斷path數組中的元素是否達到題目要求的標準，才加入result數組，所以做出的改變就是，在for循環的過程中，每一次循環都需要加當前的數組加入result中。

代碼實現

class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums,int startindex){if(path.size() == 0) result.push_back(path);if(path.size() == nums.size()){return;}for(int i = startindex;i < nums.size();i++){path.push_back(nums[i]);result.push_back(path);backtracking(nums,i + 1);path.pop_back();}return;}vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums,0);return result;}
};

LeetCode 90 子集II?

題目描述

給你一個整數數組?nums?，其中可能包含重復元素，請你返回該數組所有可能的子集（冪集）。

解集?不能?包含重復的子集。返回的解集中，子集可以按?任意順序?排列。

示例 1：

輸入：nums = [1,2,2]
輸出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

輸入：nums = [0]
輸出：[[],[0]]

思路

? ? ? ? 子集一問題和子集二問題的區別在于子集二需要進行剪枝。而如何進行剪枝和前面的組合問題是一樣的步驟。要去重的是“同一樹層上的使用過”，如何判斷同一樹層上元素（相同的元素）是否使用過了呢。

如果nums[i] == nums[i - 1]?并且?used[i - 1] == false，就說明：前一個樹枝，使用了nums[i - 1]，也就是說同一樹層使用過nums[i - 1]。

此時for循環里就應該做continue的操作。

這塊比較抽象，如圖：

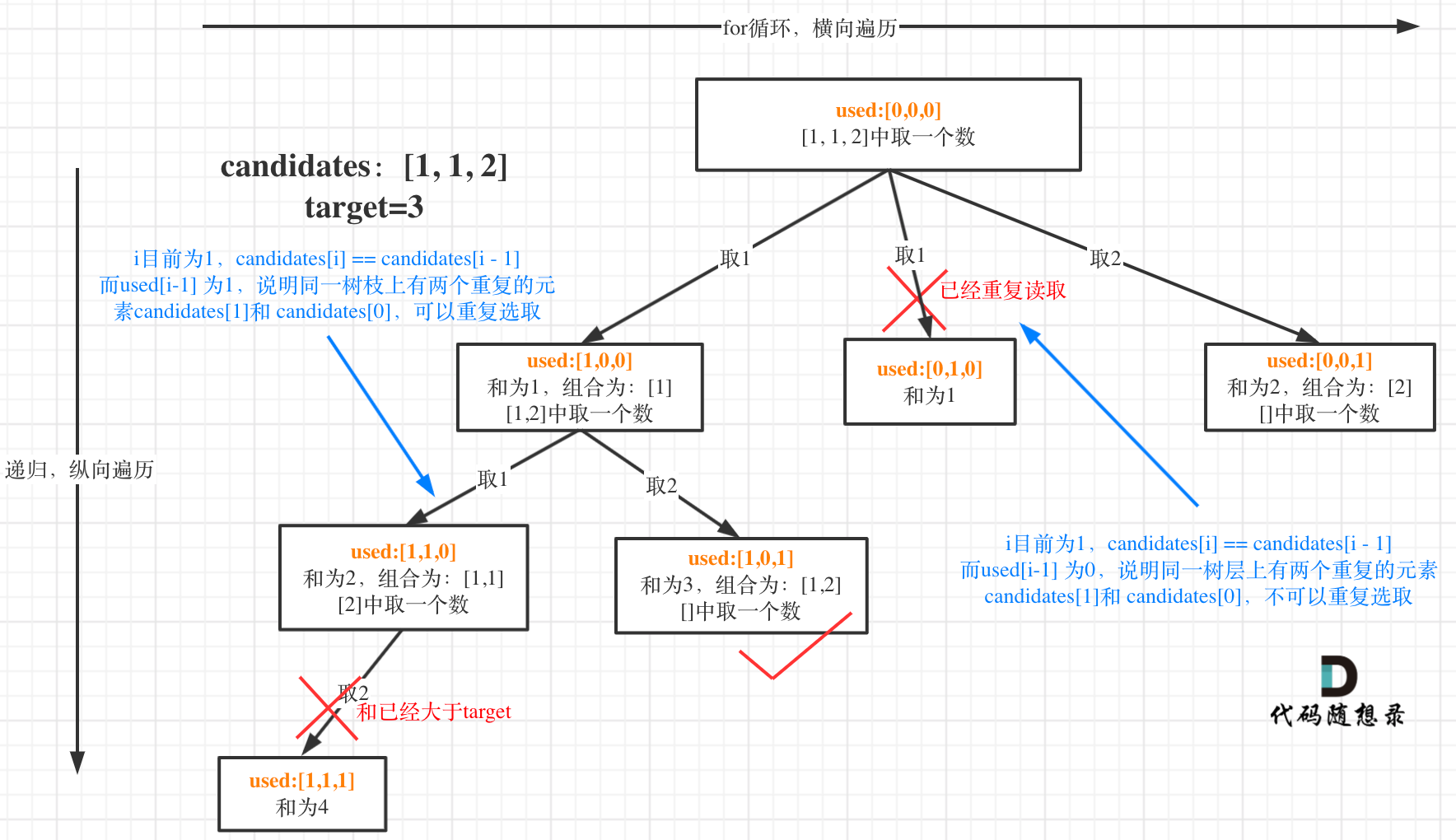
可以看出在nums[i] == nums[i - 1]相同的情況下：

• used[i - 1] == true，說明同一樹枝nums[i - 1]使用過
• used[i - 1] == false，說明同一樹層nums[i - 1]使用過

used[i - 1] = false說明已經進入另一個樹枝，所以前一個數才會被跳過，沒有遍歷到。而 used[i - 1] == true，說明是進入下一層遞歸，去下一個數，所以是樹枝上，如圖所示：

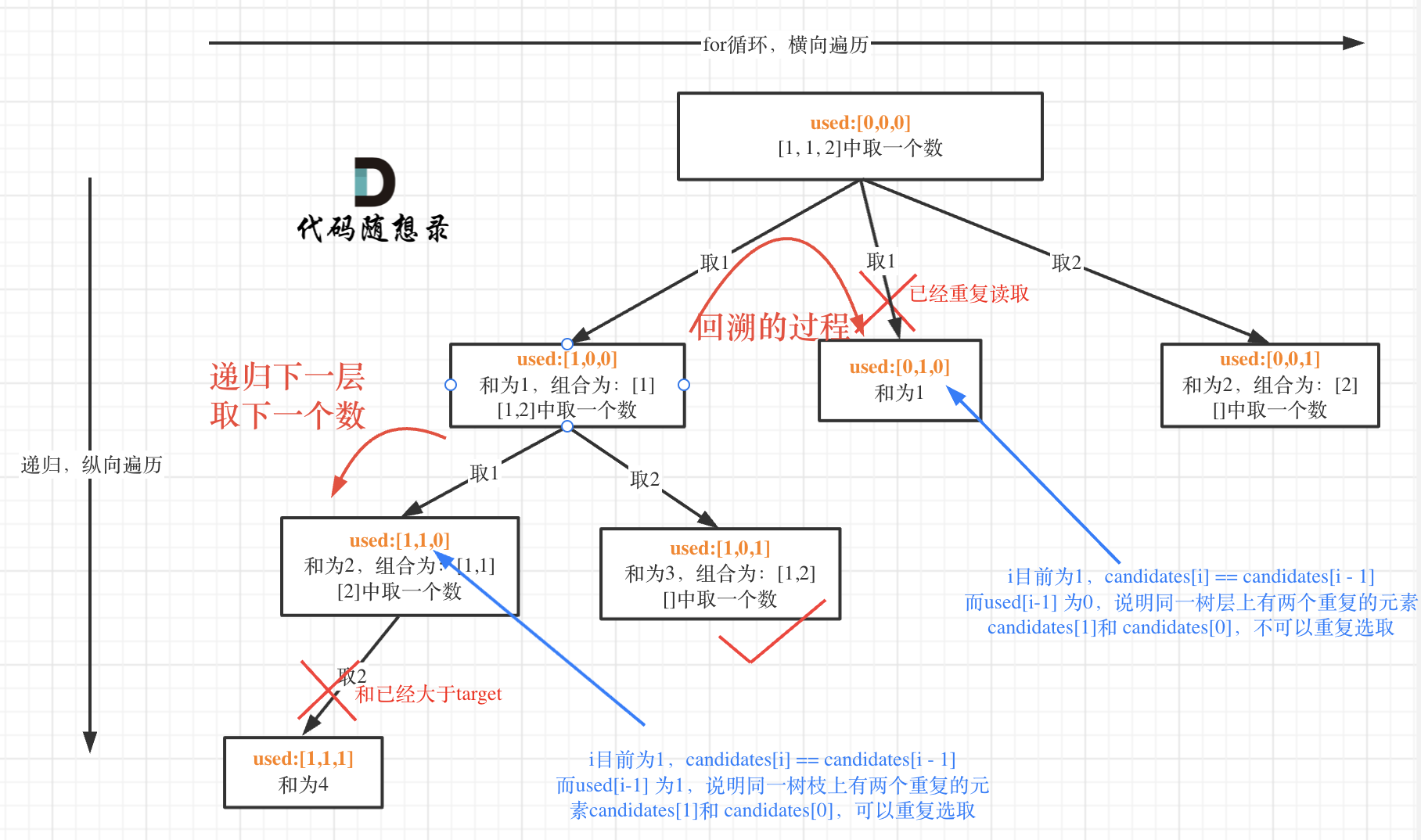
代碼實現

class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums,int startindex,vector<bool>& used){if(path.size() == 0) result.push_back(path);if(path.size() == nums.size()) return;for(int i = startindex;i < nums.size();i++){if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false){continue;}path.push_back(nums[i]);result.push_back(path);used[i] = true;backtracking(nums,i + 1,used);path.pop_back();used[i] = false;}return;}vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<bool> used(nums.size(),false);sort(nums.begin(),nums.end());backtracking(nums,0,used);return result;}
};

?LeetCode 491 非遞減子序列

題目描述

給你一個整數數組?nums?，找出并返回所有該數組中不同的遞增子序列，遞增子序列中?至少有兩個元素?。你可以按?任意順序?返回答案。

數組中可能含有重復元素，如出現兩個整數相等，也可以視作遞增序列的一種特殊情況。

示例 1：

輸入：nums = [4,6,7,7]
輸出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

輸入：nums = [4,4,3,2,1]
輸出：[[4,4]]

思路

• 遞歸函數參數

本題求子序列，很明顯一個元素不能重復使用，所以需要startIndex，調整下一層遞歸的起始位置。

代碼如下：

vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex)

• 終止條件

本題其實類似求子集問題，也是要遍歷樹形結構找每一個節點，所以可以不加終止條件，startIndex每次都會加1，并不會無限遞歸。

但本題收集結果有所不同，題目要求遞增子序列大小至少為2，所以代碼如下：

if (path.size() > 1) {result.push_back(path);// 注意這里不要加return，因為要取樹上的所有節點
}

• 單層搜索邏輯

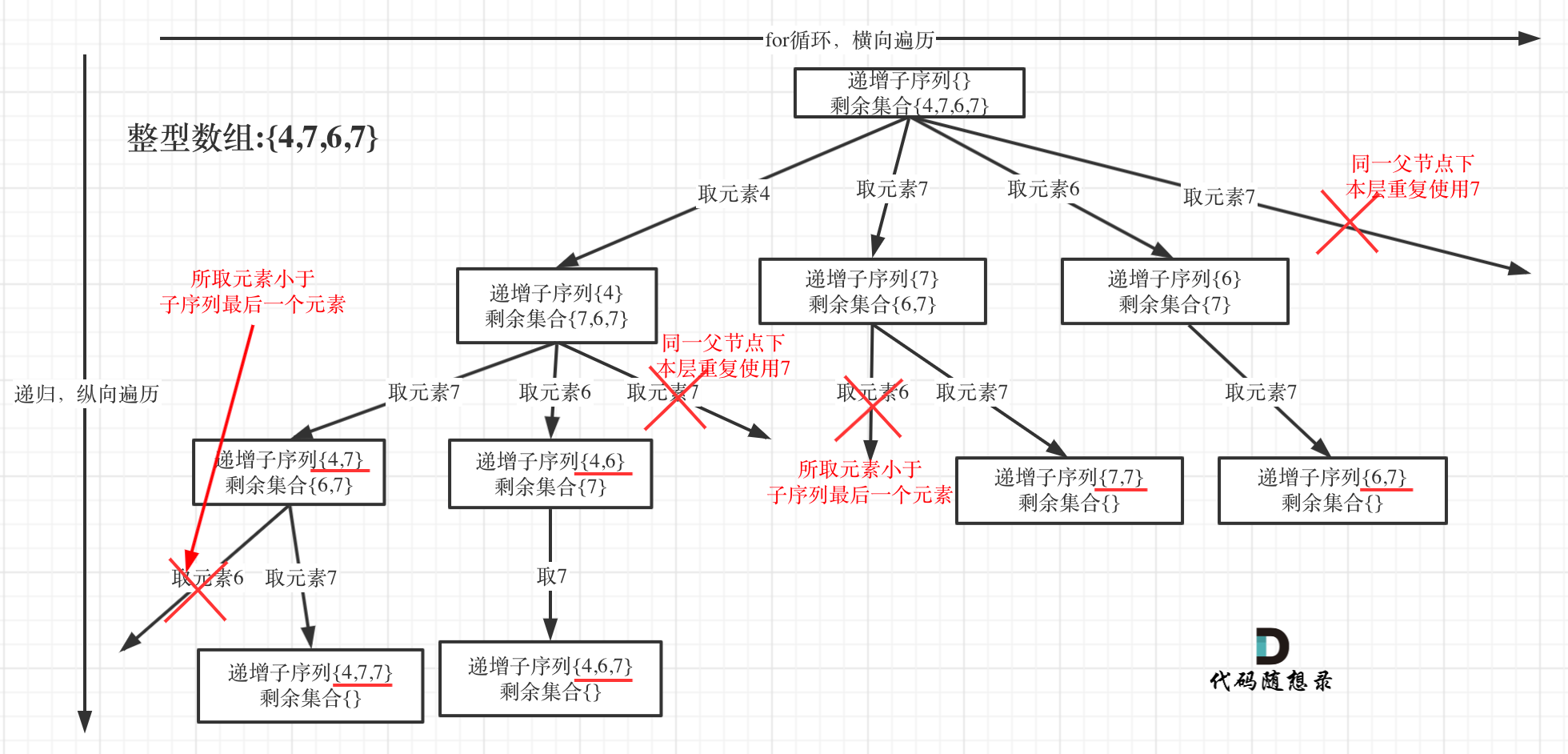
?在圖中可以看出，同一父節點下的同層上使用過的元素就不能再使用了。這里避免重復的思路是使用一個unoedered set去判斷某一數字在當前樹層是否使用過。

那么單層搜索代碼如下：

unordered_set<int> uset; // 使用set來對本層元素進行去重
for (int i = startIndex; i < nums.size(); i++) {if ((!path.empty() && nums[i] < path.back())|| uset.find(nums[i]) != uset.end()) {continue;}uset.insert(nums[i]); // 記錄這個元素在本層用過了，本層后面不能再用了path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();
}

代碼實現

class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums,int startindex){if(path.size() > 1){result.push_back(path);}unordered_set<int> uset;for(int i = startindex;i < nums.size();i++){if((!path.empty() && nums[i] < path.back())|| uset.find(nums[i]) != uset.end()){continue;}uset.insert(nums[i]); path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}vector<vector<int>> findSubsequences(vector<int>& nums) {backtracking(nums, 0);return result;}
};