
目錄
一.前言
二.樹概念及結構
2.1 樹的概念
2.2 樹的相關概念
2.3 樹的表現
2.4 樹在實際中的應用(表示文件系統的目錄樹結構)
三.二叉樹的概念及結構
3.1 概念
3.2 特殊的二叉樹
3.3?二叉樹的性質
3.4 二叉樹的存儲結構
3.4.1 順序存儲
3.4.2 鏈式存儲
四.二叉樹順序結構及實現
4.1 二叉樹的順序結構
4.2 堆的概念及結構
4.3 堆的實現
4.3.1 堆向下調整算法(略)
4.3.2 堆的創建(略)
4.3.3 建堆時間復雜度(略)
4.3.4 堆的插入(略)
4.3.5 堆的刪除(略)
4.3.6 堆代碼的實現(詳)
?4.3.6.1初始化函數
4.3.6.2 銷毀函數
4.3.6.3 插入函數
4.3.6.4 向上調整函數
4.3.6.5?交換函數
?4.3.6.6打印函數
4.3.6.6 刪除函數
4.3.6.7 向下調整函數
4.3.6.8 獲取根值函數
4.3.6.9 判空函數
4.3.6.10 堆排序?
4.3.6.11向下調整去建堆
4.3.6.12 建堆復雜度的證明?
4.3.6.13 小練習(選看)
五.全部代碼
六.結語
 一.前言
一.前言
友情提醒:本文前面對概念涉及頗深,如果有友友了解二叉樹的基本概念,想要看核心代碼實現可以直接翻找目錄移至四.二叉樹順序結構及實現片段開始閱讀。碼字不易,希望大家多多支持我呀!(三連+關注,你是我滴神!)
二.樹概念及結構
2.1 樹的概念
樹是一種非線性的數據結構,它是由n(n>=0)個有限節點組成一個具有層次關系的集合,把它叫做樹是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
- 有一個特殊的結點,稱為根結點,根結點沒有前驅結點。
- 除根結點外,其余結點被分為m(m>0)個互不相交的集合T1、T2、... 、Tm,其中每一個集合Ti(1<=i<=m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅,可以有0個或多個后繼。
- 因此,樹是遞歸定義的。
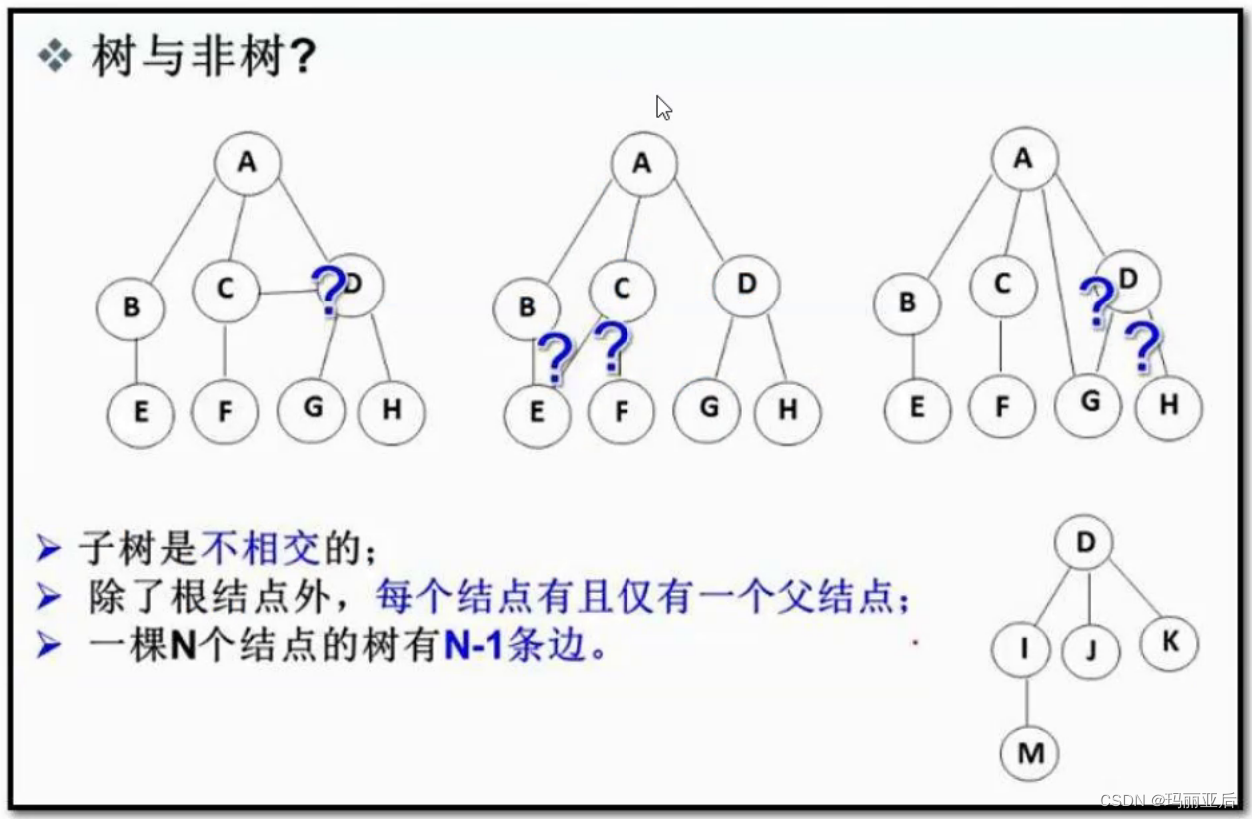
注意:樹形結構中,子樹之間不能有交集,否則就不是樹形結構。
2.2 樹的相關概念
下面有一些關于樹的術語,大家如有疑惑可以看此解析
結點的度:一個結點含有的子樹的個數稱為該結點的度;如上圖:A的為6
葉結點或終端結點:度為0的結點稱為葉結點;如上圖:B、C、H、I...等結點為葉結點
非終端結點或分支結點:度不為0的結點;如上圖:D、E、F、G...等結點為分支結點
雙親結點或父結點:若一個結點含有子結點,則這個結點稱為其子結點的父結點;如上圖:A是B的父結點
孩子結點或子結點:一個結點含有的子樹的根結點稱為該結點的子結點;如上圖:B是A的孩子結點
兄弟結點:具有相同父結點的結點互稱為兄弟結點;如上圖:B、C是兄弟結點
樹的度:一棵樹中,最大的結點的度稱為樹的度;如上圖:樹的度為6
結點的層次:從根開始定義起,根為第一層,根的子結點為第二層,以此類推
樹的高度或深度:樹中結點的最大層次;如上圖:樹的高度為4
堂兄弟結點:雙親在同一層的結點互為堂兄弟;如上圖:H、I互為兄弟結點
結點的祖先:從根到該結點所經分支上的所有結點;如上圖:A是所有結點的祖先
子孫:以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖:所有結點都是A的子孫
森林:由m(m>0) 棵互不相交的樹的集合稱為森林
2.3 樹的表現
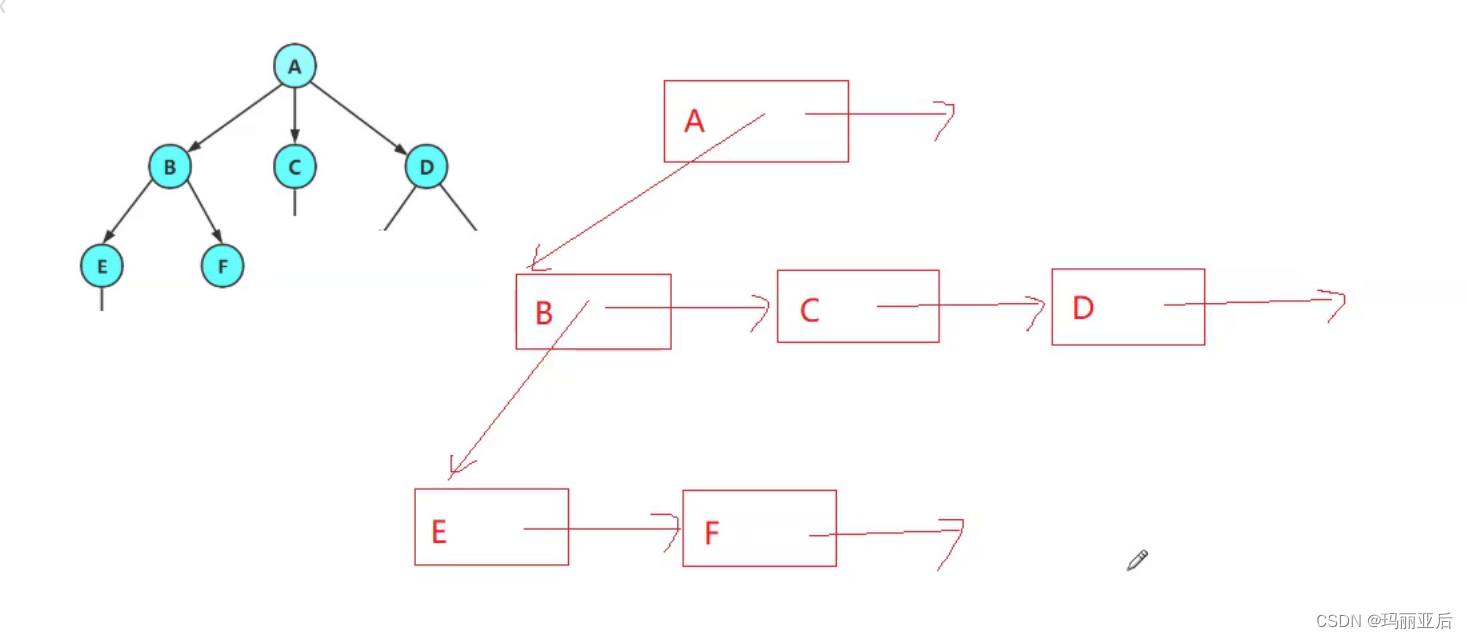
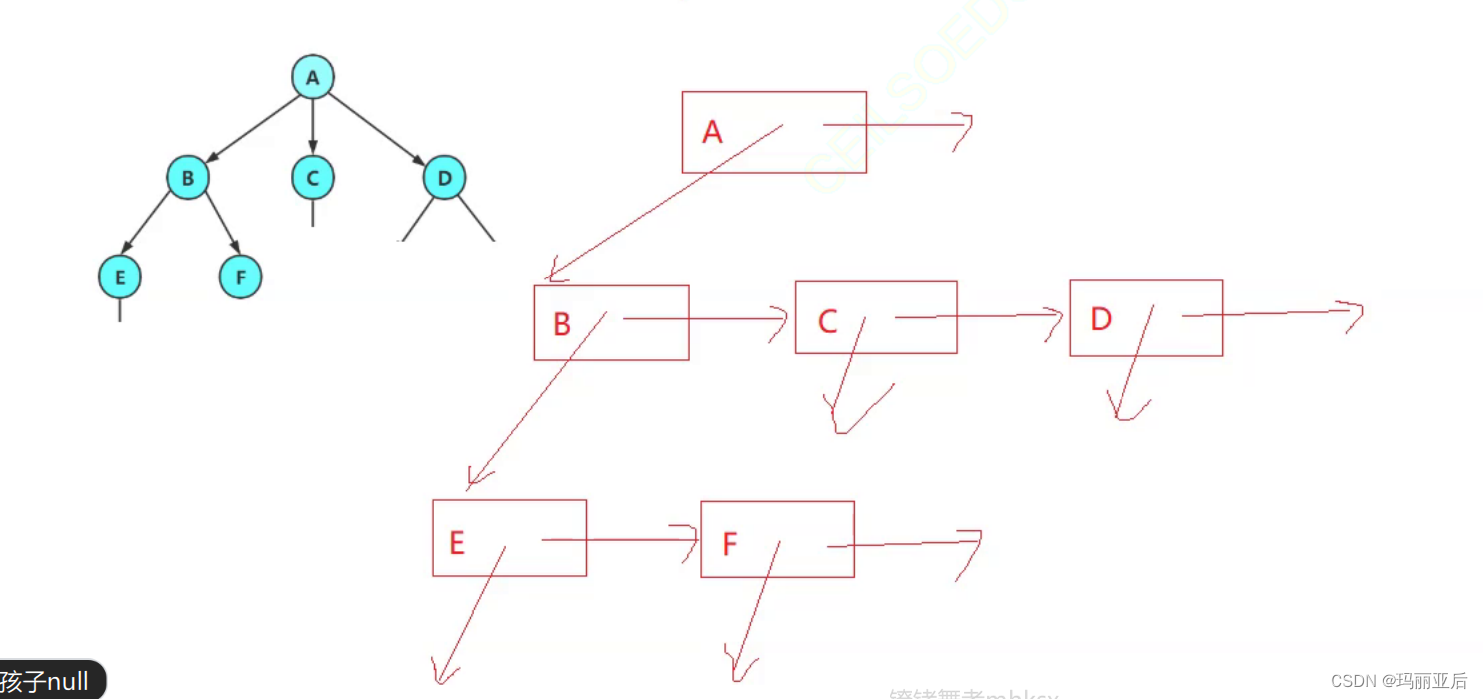
左孩子右兄弟表示法:當A生了3個孩子:B C D時,永遠指向最左邊的孩子(B),然后讓孩子B去帶孩子C,孩子C去帶孩子D。
A只生了3個孩子,所以最后的孩子D指向空,而A也沒有兄弟,那么根據左孩子右兄弟的指法,A右邊也指向空。
最后再看向E F,B有兩個孩子是E與F,根據右孩子所以指向最右邊的孩子E,而E有兄弟F,根據右兄弟E指向F,最后F指向空。
那么最后我們如何判斷一個結點是不是葉子呢?只需要看(firstchild)是否為空就行了。
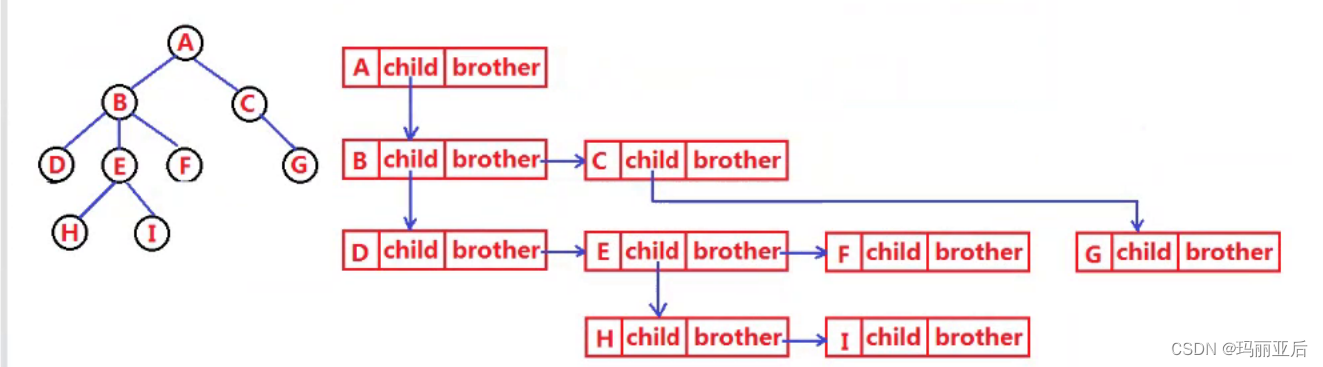
樹結構相對線性表就比較復雜了,要存儲表示起來比較麻煩,既要保存值域,也要保存結點和結點之間的關系,實際中樹有很多種表示方法如:雙親表示法,孩子表示法,孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單地了解其中最常用的孩子兄弟表示法。?
//樹的最優設計 struct TreeNode {int val; //結點中的數據域struct TreeNode* firstchild; //第一個孩子結點struct TreeNode* nextbrother;//指向其下一個兄弟結點 };
孩子兄弟法演示圖:?
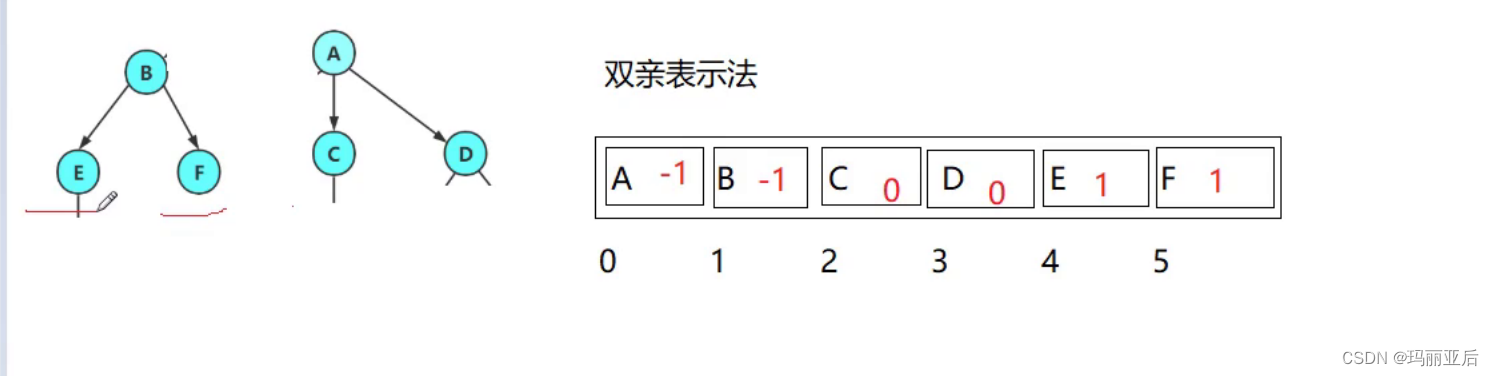
拓展:雙親表示法演示圖?
- 判斷有幾棵樹——(看幾個-1)。因為A和B找不到父親的下標就給數值-1。
- 判斷兩個結點在不在同一棵樹(看根一不一樣)。通過對比所在父親的下標是否相同來判斷。
注:鏈式結構看指針,下標看數組
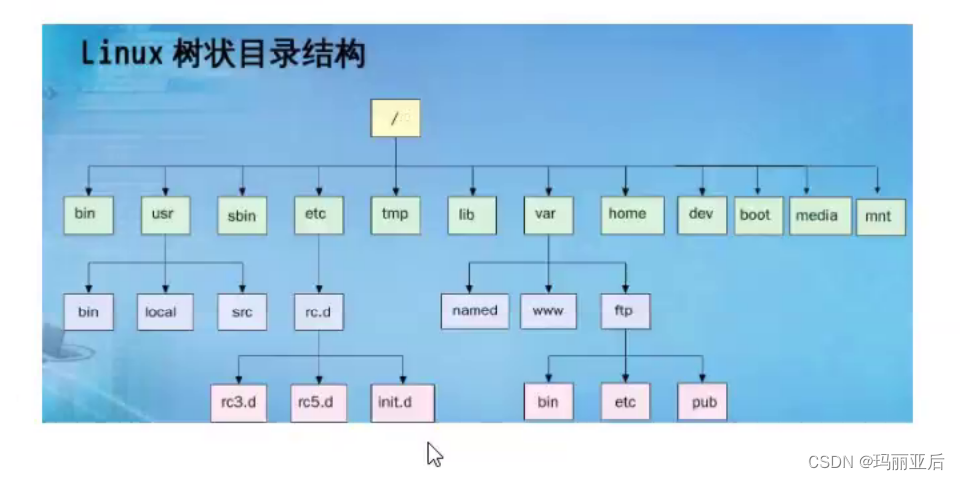
2.4 樹在實際中的應用(表示文件系統的目錄樹結構)
三.二叉樹的概念及結構
3.1 概念
一棵二叉樹是結點的一個有限集合,該集合:
- 或者為空
- 由一個根結點加上兩棵別稱為左子樹和右子樹的二叉樹組成
從上圖可以看出:
- 二叉樹不存在度大于2的結點
- 二叉樹的子樹有左右之分,次序不能顛倒,因此二叉樹是有序樹
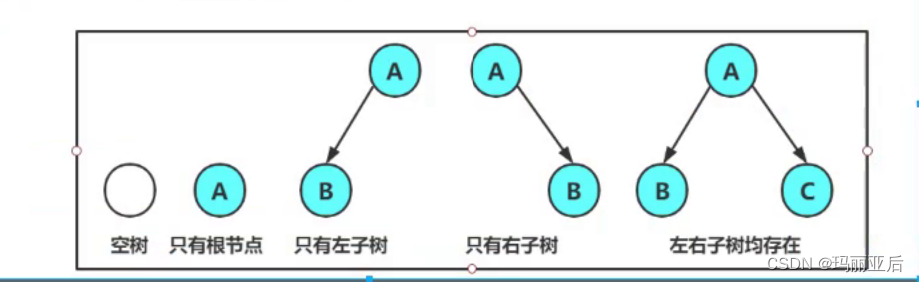
注意:對于任意的二叉樹都是由以下幾種情況復合而成的:
3.2 特殊的二叉樹
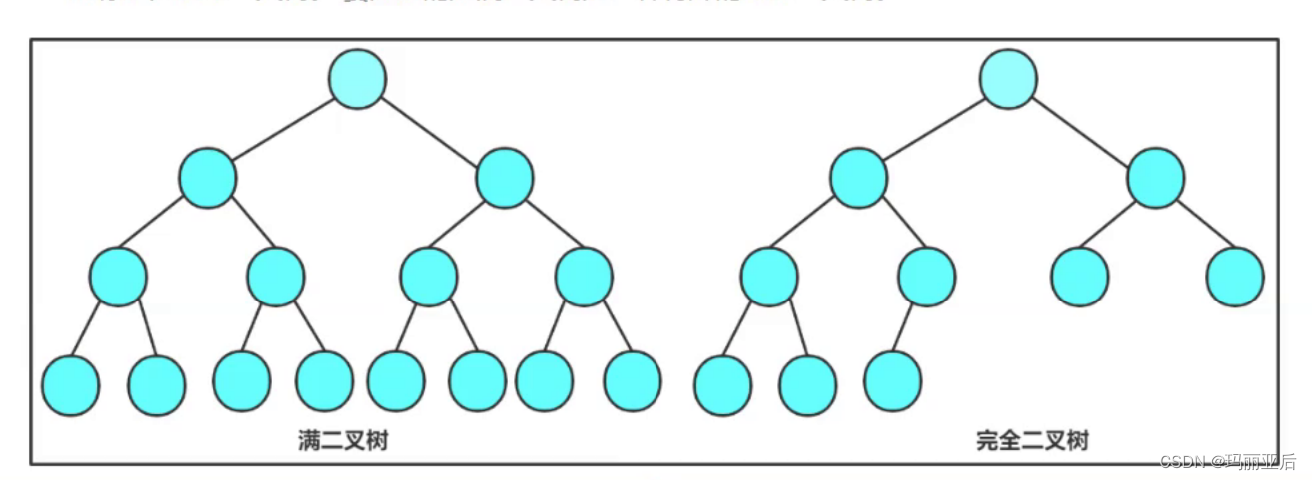
- 滿二叉樹:一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。也就是說,如果一個二叉樹的層數為K,且結點總數是2^k-1,則它就是滿二叉樹。
- 完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對于深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點——對應時稱之為完全二叉樹。要注意的是滿二叉樹是一種特殊的完全二叉樹。
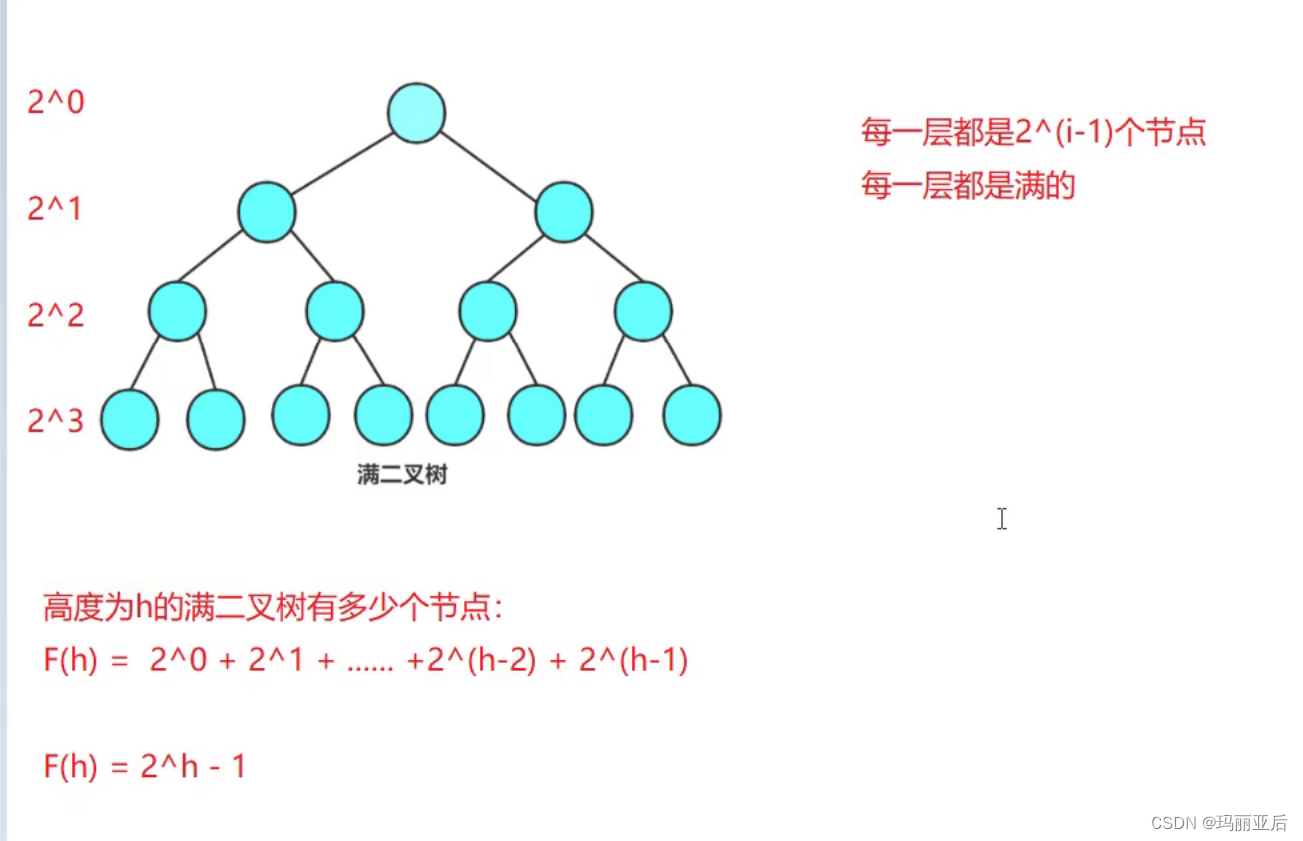
假設它的高度是h,每一層都是滿的。
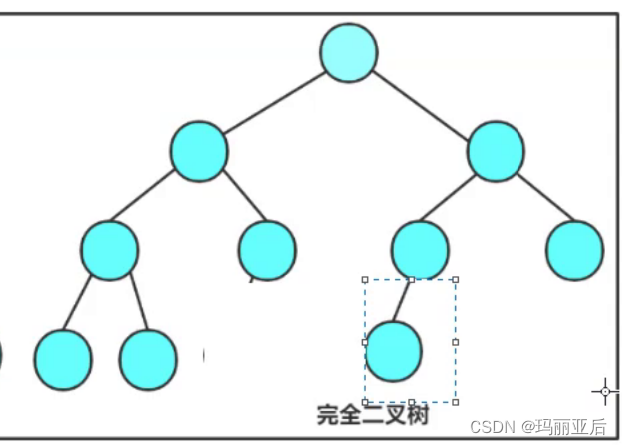
假設它的高度是h,前h-1層是滿的,最后一層不一定滿,從左到右是連續的。
比如我們移動一個結點后最后一層不再是連續的了,那就不叫做完全二叉樹。?
下面我們來看看在高度為h中二叉樹的結點數是多少~
我們還可以通過結點來反推高度h
至于高度為h的完全二叉樹的結點范圍,最多結點那就是跟滿二叉樹一樣(2^h-1)
那最少結點呢?我們可以把它拆成高度為h-1的滿二叉樹,此時結點為(2^(h-1)-1)。最后在h層添上一個節點就是最少結點(2^(h-1))?
3.3?二叉樹的性質
- 若規定根結點的層數為1,則一棵非空二叉樹的第i層上最多有2^(i-1)個結點
- 若規定根結點的層數為1,則深度為h的二叉樹的最大結點數是2^h-1
- 對任何一棵二叉樹,如果度為0其葉結點個數為n0,度為2的分支結點個數為n2,則有n0=n2+1
- 若規定根結點的層數為1,具有n個結點的滿二叉樹的深度,
- 對于具有n個結點的完全二叉樹,如果按照從上至下從左至右的數值順序對所有結點從0開始編號,則對于序號為i的結點有:
- 若i>0, i位置結點的雙親序號:(i-1)/2;i=0;i為根結點編號,無雙親結點
- 若2i+1<n,? ?左孩子序號:2i+1,? 2i+1>=n否則無左孩子
- 若2i+2<n,右孩子序號:2i+2,2i+2>=n否則無右孩子
下面來幾道練習題~?
第一問:葉子結點就是度為0的點,通過n0=n2+1公式可以得出為200個,故選A。
第二問:非完全二叉樹不適合,會空出數組位置。故選A
第三問:
N1只能是1,因為n只能是整數,故選A。
第四問:
我們可以根據完全二叉樹結點數的范圍來判斷h為多少(把h代入看是否超過范圍)。故選B
第五問:
跟第三問一樣的特點,只不過767是一個奇數,所以N1只能取0.故選B
3.4 二叉樹的存儲結構
二叉樹一般可以使用兩種結構存儲,一種順序結構,一種鏈式結構。
3.4.1 順序存儲
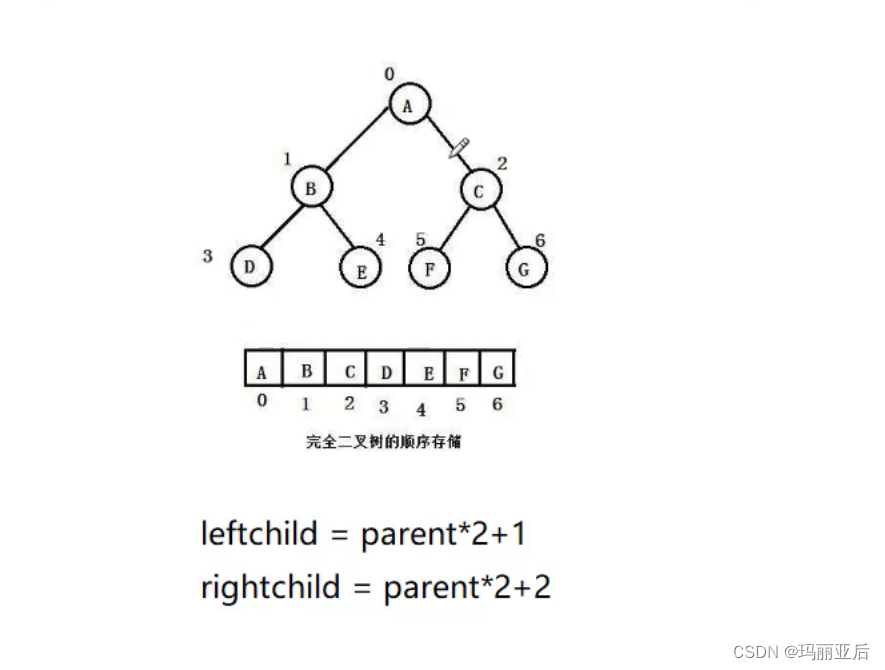
順序結構存儲就是使用數組來存儲,一般使用數組只適合表示完全二叉樹,因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲,二叉樹順序存儲在物理上是一個數組,在邏輯上是一棵二叉樹。
左孩子為其父親所示下標*2+1,右孩子為父親所示下標*2+2.反過來孩子其父親的坐標也可以反推——parent = (child-1)/2
注:右孩子都在偶數位上,但6-1=5,5/2還是2公式還是可以用
任意位置通過下標可以找父親或者孩子
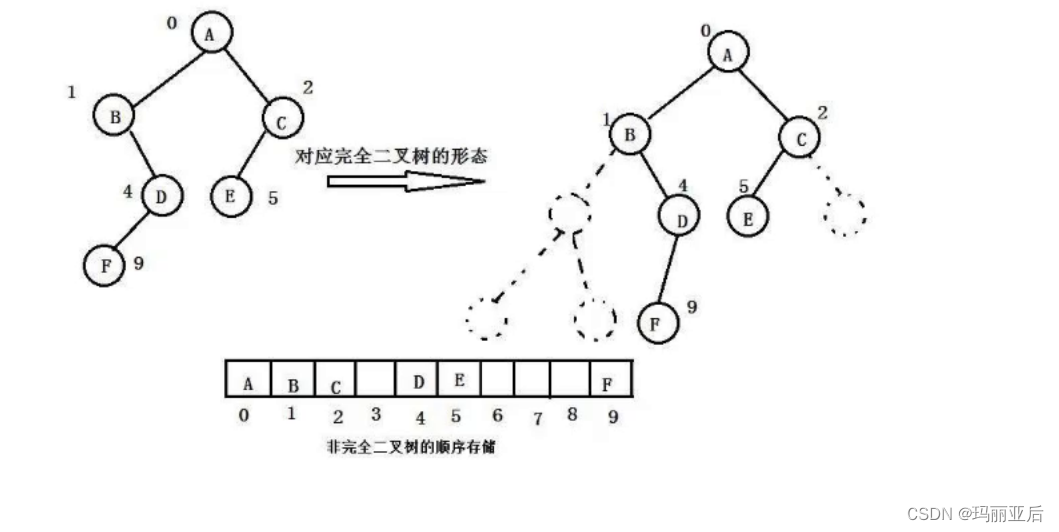
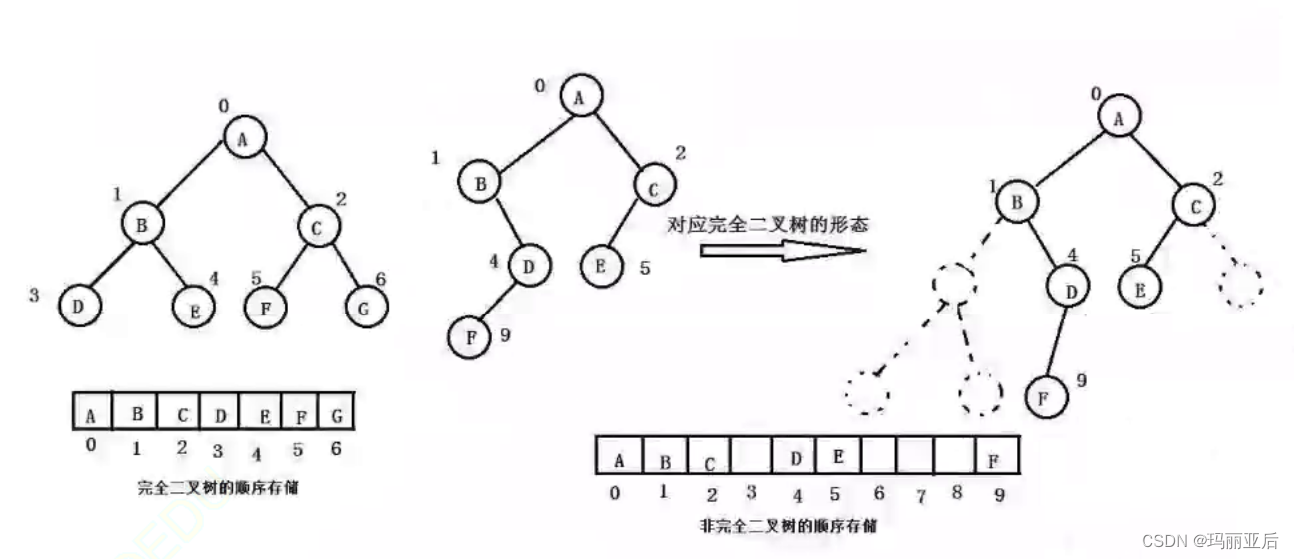
如果是不完全二叉樹適不適合用該存儲結構呢?——不適合用這樣的結構(數組存儲)
滿二叉樹或者完全二叉樹適合,不完全二叉樹適合用鏈式結構存儲
3.4.2 鏈式存儲
二叉樹的鏈式存儲結構是指,用鏈表來表示一棵二叉樹,即用鏈來指示元素的邏輯關系。通常的方法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別用來給該結點左孩子和右孩子所在的鏈結點的存儲地址。鏈式結構又分為二叉鏈和三叉鏈,當前我們學習中一般都是二叉鏈。
四.二叉樹順序結構及實現
4.1 二叉樹的順序結構
普通的二叉樹是不適合用數組來存儲的,因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結構存儲。現實中我們通常把堆(一種二叉樹)使用順序結構的數組來存儲,需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事,一個是數據結構,一個是操作系統中管理內存的一塊區域分段。
4.2 堆的概念及結構
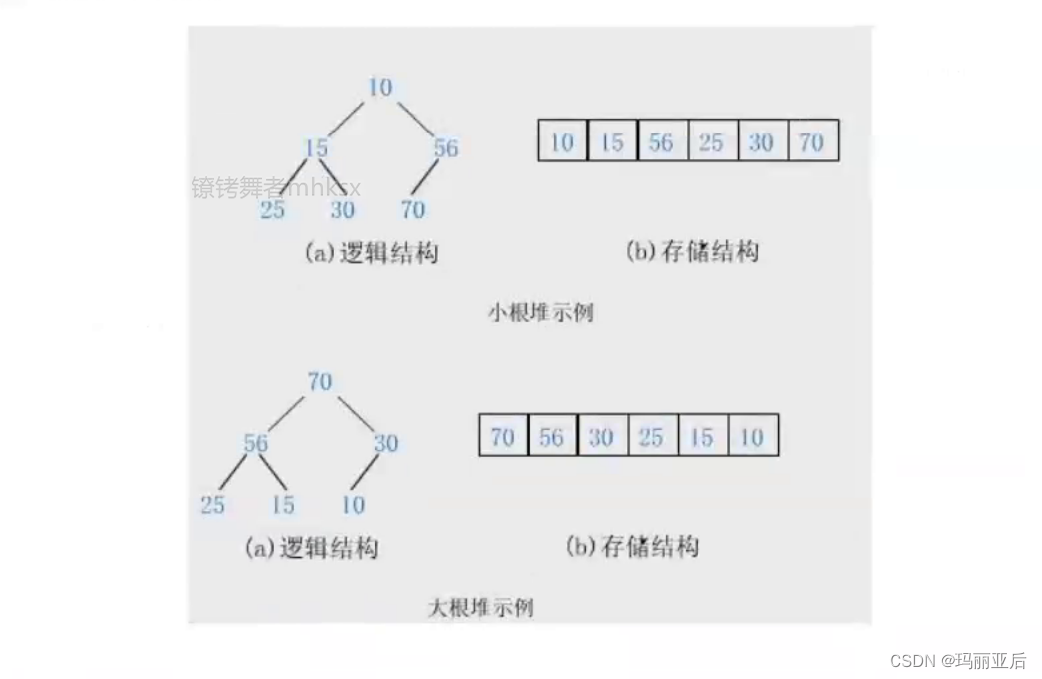
如果有一個關鍵碼的集合k={k0,k1,k2,...k(n-1)},把它的所有元素按完全二叉樹的順序存儲方式存儲在一個一維數組中,并滿足:ki<=k()2i+1)且ki<=k(2i+2)? ?(ki>=k(2i+1)且ki>=k(2i+2)) i=0,1,2...,則稱為小堆(或大堆)。將根結點最大的堆叫做最大堆或大根堆,根結點最小的堆叫做最小堆或小根堆。
堆的性質:
- 堆中某個結點的值總是不大于或不小于其父結點的值;
- 堆總是一棵完全二叉樹。
注:說的是數值而不是下標
我們來用練習題來體會其中的規律~
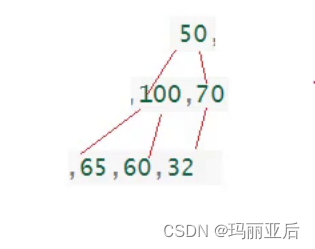
選項A:我們先按照完全二叉樹的定義把堆給表現出來(注意連續),后面發現這是大堆(樹中任意一個父親都>=孩子)
選項D:我們會發現從上面是一個小堆,而下面又是一個大堆,這是明顯矛盾的,所以判定為錯誤。
底層:
- 物理結構,數組
- 邏輯結構,完全二叉樹
問:如果是小堆,那底層數組是否升序呢?——不一定~
但可以確定的是小堆的根是整棵樹的最小值。
堆的運用:
- topk問題
- 堆排序(時間復雜度——O(N*logN)
————————————————————————————————以上都是概念。
4.3 堆的實現
4.3.1 堆向下調整算法(略)
4.3.2 堆的創建(略)
4.3.3 建堆時間復雜度(略)
4.3.4 堆的插入(略)
4.3.5 堆的刪除(略)
4.3.6 堆代碼的實現(詳)
?4.3.6.1初始化函數
//初始化函數 void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0;}這是我們的老朋友了,基本每篇文章都寫一遍哈哈~?
另一種初始化函數
//另一種初始化函數 void HeapInitArray(HP* php, int* a, int n) {assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}php->size = 0;php->capacity = 0;memcpy(php->a, a, sizeof(HPDataType) * n);for (int i = 1; i < n; i++){AdjustUp(php->a, i);} }直接給你一個數組,然后把這個數組直接插入堆里面去。原先的初始化是不給值,然后一個一個慢慢插入堆?
4.3.6.2 銷毀函數
//銷毀函數 void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0; }
4.3.6.3 插入函數
?
?假設我們插入的數是90,在小堆中剛好可以直接插入,不需要做其他的變動。
那如果我們插入50呢?這樣就破壞的小堆的結構了,所以我們需要調整插入的位置。按照小堆的規則我們不可能去向下進行調整,那只好去找上面的結點了~
所以我們現在就要去找該結點的父親位置了,通過公式(child-1)/2推出父親為下標2的56。
找到后如果該結點比它父親大,那就不動,如果小,那么就得交換位置。相當于讓50當父親,56當兒子,這樣才能維持小堆結構。
當然這樣還不算結束,我們交換完還得再跟10這個根進行比較,完成上述操作后才可以算是達成小堆的結構。
最壞情況是要調到根才結束,
//插入函數 void HeapPush(HP* php, HPDataType x) {assert(php);//擴容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);//不僅要把數組傳過去,我們還得把孩子也傳過去,而孩子可以通過下標找到}擴容和插入都是很常見的操作了,在成功插入后(尾插),我們還得去做向上的一個調整(畢竟插入后并不能保證可以維持原來小堆或大堆的結構)。
PS:?之所以要傳尾部是因為我們插入的數據是在尾部,所以得從該數據插入起進行調整。
4.3.6.4 向上調整函數
當發現插入的孩子小于父親時,進行交換。然后再讓5去當孩子繼續和新的父親10進行對比。
那要在什么時候才算是結束調整呢?在最壞情況下,孩子5與父親10發現交換,child指向5,而parent則指向數組外,說明當parent小于0時就代表無需調整。
但是這里有一點需要注意,如果按照孩子5已經為根(child==0)的計算規則其父親下標為(child-1)/2,結果將會是0.而不是-0.5,那代表調整還未結束,發生矛盾。
所以我們這里調整結束的條件改為(child>0),當child等于0也意味著調整結束了。
//向上調整函數 void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}} }
4.3.6.5?交換函數
//交換函數 void Swap(HPDataType* p1, HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp; }
?4.3.6.6打印函數
//打印函數 void HeapPrint(HP* php) {assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");}
做完以上這些函數,我們就來測試一下:
int main() {int a[] = { 65, 100, 70, 32, 50, 60 };HP hp;HeapInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}HeapDestroy(&hp);return 0; }
測試完畢,插入后進行調整還是小堆~
PS:我們這里的插入是額外開辟一個空間然后從數組里面取值,在開辟的空間里一個一個插入。
4.3.6.6 刪除函數
有一個問題,在堆的刪除中,我們刪除誰比較有意義呢?
如果只是刪除尾,那沒有什么意義~最有意義的就是刪除根,至于為什么,下面就來演示一番~
注:挪動覆蓋數組的方式并不可取,這樣無法保證小堆原有的結構。
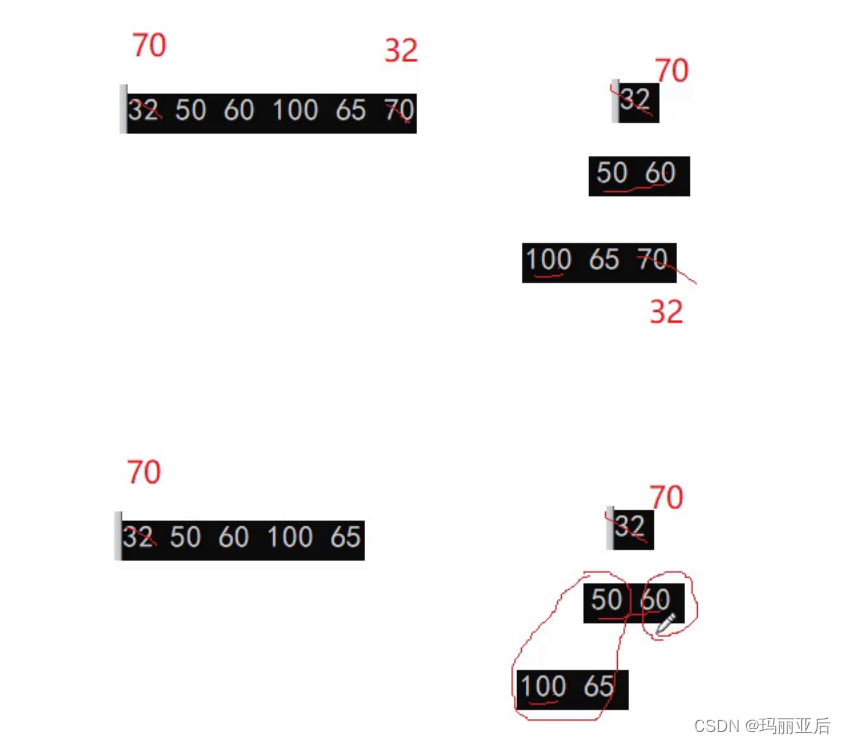
我們可以這樣操作:讓根與尾的數據進行交換,再刪除,這樣的好處是不會破壞原有的左右子樹的小堆結構。
然后我們再根據新的根進行向下調整來維持小堆的結構,注:無論是向下調整還是向上調整,它們的前提都是左右子樹為小堆或大堆。
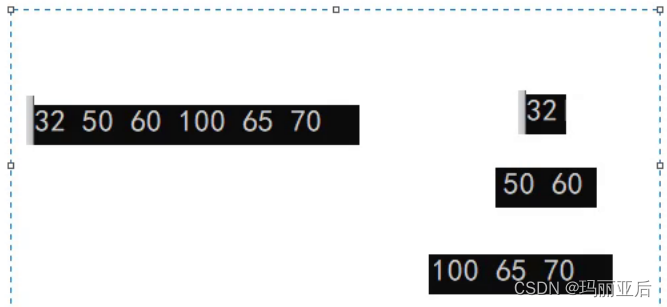
向下調整:我們先找出根下面的左右兩個孩子,然后和二者中最小的進行對比,這里左孩子50比右孩子60更小,讓根70與左孩子50作對比,發現左孩子比根還小,按照小堆的規則兩者需要進行交換。
以此類推,直到最后和葉子65進行對比。向下調整就是把小的往下調,大的往下沉這樣一個過程。
其實這里的Pop還有另外一層意義——找出當前二叉樹中最小的值。
時間復雜度:O(logN) 具有極高效率的算法排序
//刪除函數 void HeapPop(HP* php) {assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//刪除數據AdjustDown(php->a, php->size, 0); }
4.3.6.7 向下調整函數
在這里我們不去刻意區分左孩子和右孩子,而是先假設左孩子是最小的,如果實際上是右孩子小,那就讓它們進行交換。最后換到葉子就終止。——先假設,錯誤再糾正。
//向下調整函數 void AdjustDown(HPDataType* a, int n, int parent) {//假設左右孩子中小的為左孩子int child = parent * 2 + 1;while (child<n)//換到葉子就終止,循環結束后child已經是指向數組外了{//找出小的孩子if (child+1<n&&a[child + 1] < a[child])//如果右孩子比左孩子小{child++;//小的孩子變成右孩子}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//繼續向下調整parent = child;child = parent * 2 + 1;//跟向上調整法一樣,交換完后把parent和child都移下一層為下一次的循環作準備}else{break;}} }有一點需要注意,在我們規定好child<n的條件后還要判定child+1是否在該范圍內:
就比如我們把在調整第二行80的位置時(尾部的80已經和堆頂的32交換完畢,接著80和它的右孩子40交換完畢),按照我們的代碼是會去找到child+1,可是畫圈部分根本沒有右孩子,所以為了避免它越界隨便找一個值替代,我們要再多加一個判定條件——child+1<n。
4.3.6.8 獲取根值函數
//獲取根值函數 HeapTop(HP* php) {assert(php);assert(php->size > 0);return php->a[0]; }
4.3.6.9 判空函數
//判空函數 bool HeapEmpty(HP* php) {assert(php);return php->size == 0; }
測試一下:我們去取最小、次小等等的數據
int main() {int a[] = { 65, 100, 70, 32, 50, 60 };HP hp;HeapInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}HeapPrint(&hp);while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestroy(&hp);return 0; }
最后會發現取出來的確實都是最小的,最后形成升序的結果。只要我們去修改成大堆或小堆,就可以起到降序或升序的效果~
4.3.6.10 堆排序?
當然現在這樣還不算是真正的堆排序,因為我們只是打印出來排序的堆,要想用堆實現數組本身的排序,請看如下解析:
void HeapSort(int* a, int n) {HP hp;HeapInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}int i = 0;while (!HeapEmpty(&hp)){//printf("%d ", HeapTop(&hp));//關鍵代碼,真正實現對數組內部的排序a[i++] = HeapTop(&hp);HeapPop(&hp);}HeapDestroy(&hp); }int main() {int a[] = { 65, 100, 70, 32, 50, 60 };HeapSort(a, sizeof(a) / sizeof(int));return 0; }但這種寫法有兩個大缺陷:
- 先有一個堆的數據結構
- 空間復雜度的消耗(為了排序額外開辟了一塊數組空間)
所以我們還需要進行優化:
我們不用先去開辟空間搞堆,直接把數組當成堆去看
目前數組只能說是排成堆的模樣,但還不是堆,所以我們需要對它進行調整——建堆
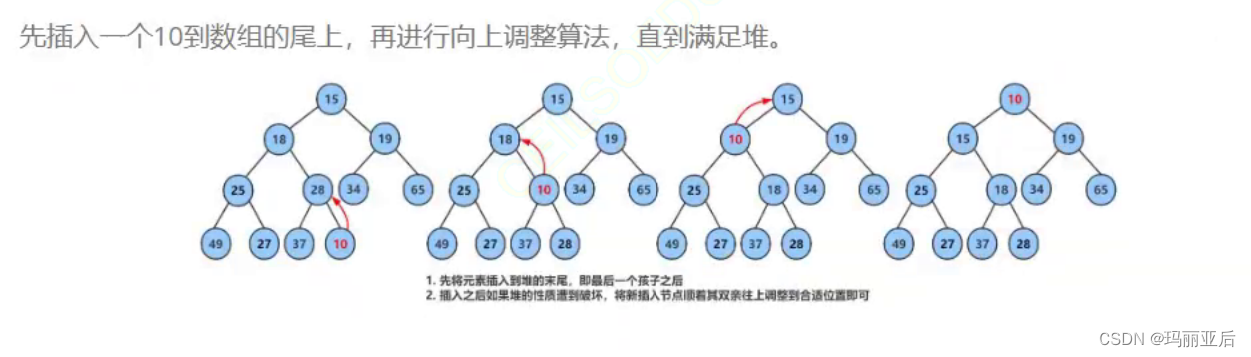
最核心的部分!!!
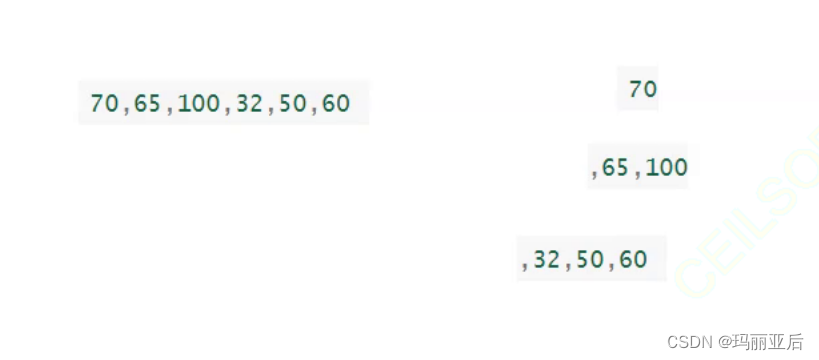
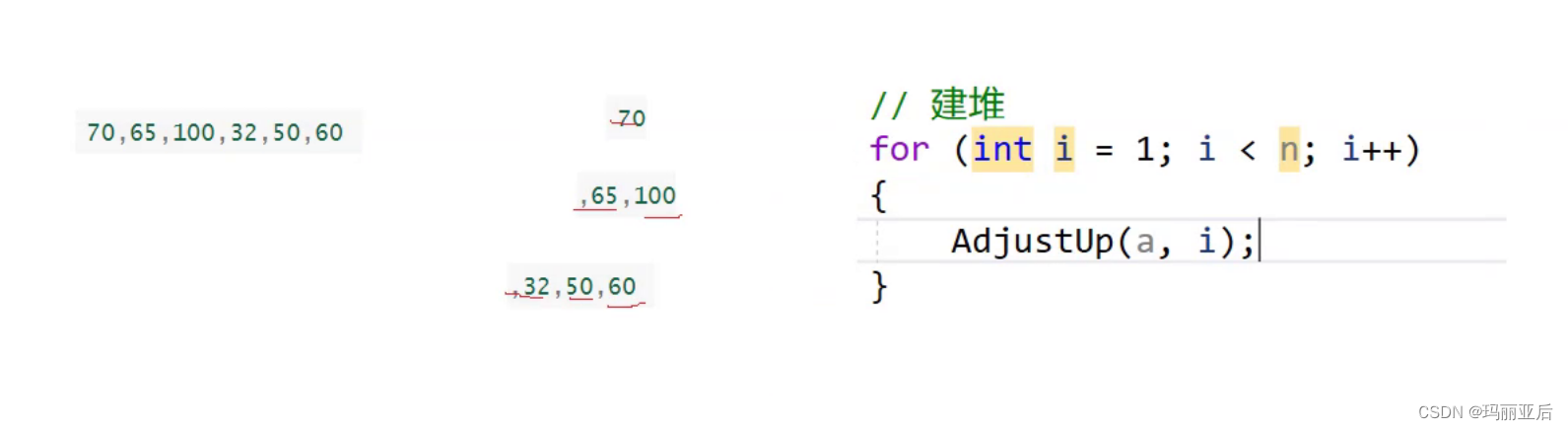
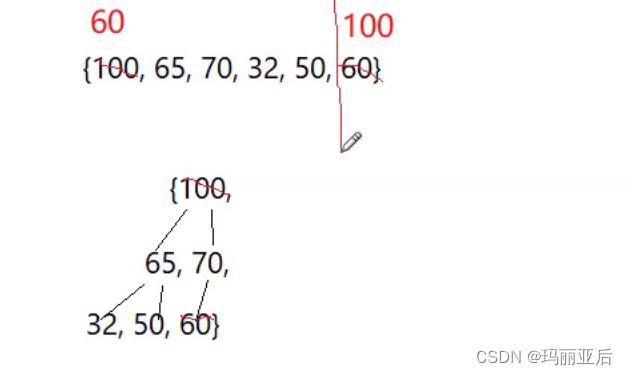
在我們前面寫的向上調整法中一般都是把最后的數據傳遞進去再進行調整整個堆,因為我們的插入算是尾插,所以傳的也只是尾部數據。而在上圖中,我們可以想象該數組只有一個數——70(自成堆),然后我們插入65進行向上調整(比如我們想要調成大堆),調整完畢后變成70——65(兩個數組成堆),就這樣以此類推地去插入數據,這樣就是建堆的關鍵!——遍歷除堆頂以外的數字,把每一次的調整都看作是尾插。
最后來驗證一下:
void HeapSort(int* a, int n) {//建堆for (int i = 0; i < n; i++){AdjustUp(a, i);} }int main() {//int a[] = { 65, 100, 70, 32, 50, 60 };int a[] = { 70, 65, 100, 32, 50, 60 };HeapSort(a, sizeof(a) / sizeof(int));return 0; }
最后達成建堆效果,也彌補了前面的兩大缺陷~接下來我們來實現排序效果~
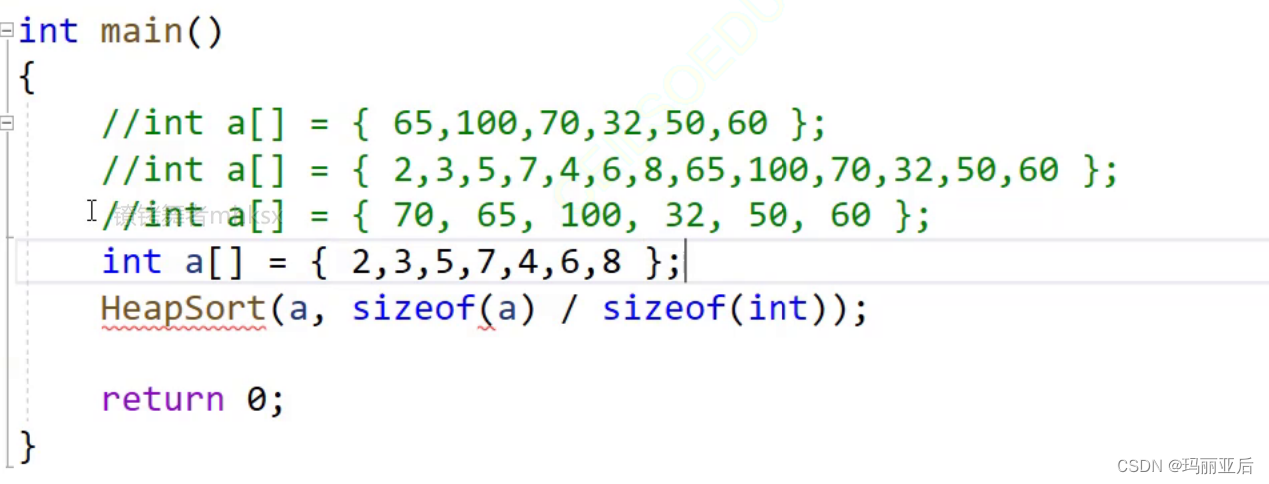
如果我們想要升序,那就要去建小堆~我們換個數組來建堆
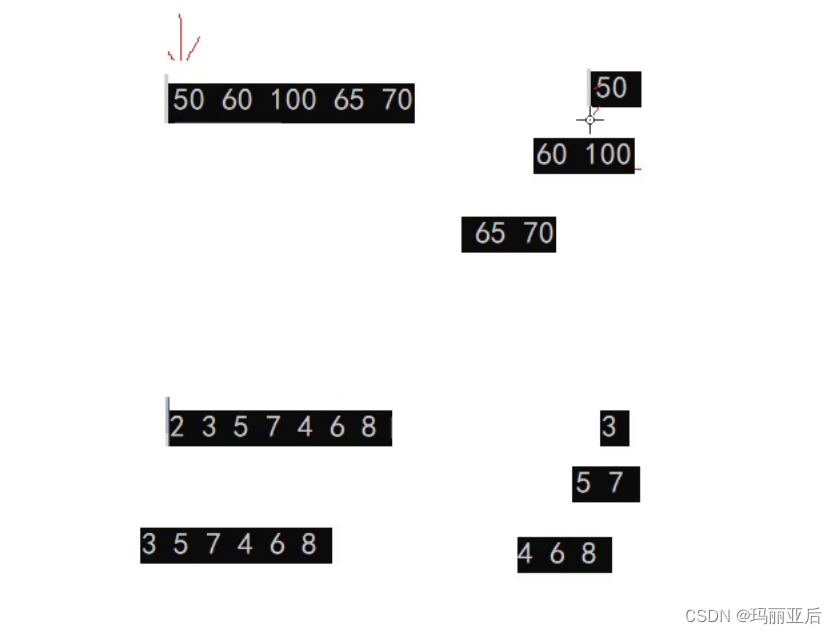
由于是升序,當我們把根(2)選出去后——選出了最小的數據,要選次小,只能把剩下的數據看作堆。但最后發現已經無法構成小堆的結構了~所以我們只能換個思路了,想要升序建小堆不行的話那就試試大堆怎么樣~
在建好大堆后用向下調整法先和尾部60進行交換,交換完不用去刪除尾部數據,而是把它從數組中隔離開來(就是無視它在數組和堆中的位置)。
然后把剩下的數據看作堆,那選次大要怎么選呢?繼續用向下調整法即可。
每一次一個數據的調整是logN,一共有N個數據,那時間復雜度就是O(N*logN)
void HeapSort(int* a, int n) {//建堆for (int i = 0; i < n; i++){AdjustUp(a, i);}//建大堆升序int end = n - 1;//數組尾部數據下標while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);//選出最大end--;//讓數組最后數據的前一位和堆頂交換} }int main() {//int a[] = { 65, 100, 70, 32, 50, 60 };//int a[] = { 70, 65, 100, 32, 50, 60 };int a[] = { 2, 3, 5, 7, 4, 6, 8 };HeapSort(a, sizeof(a) / sizeof(int));return 0; }調試內容:經過不斷調試,最終的結果為升序
?
4.3.6.11向下調整去建堆
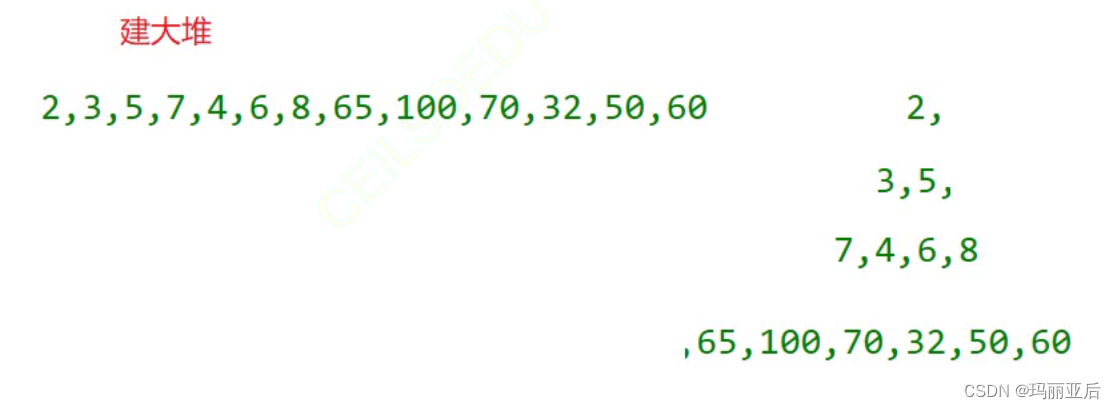
除了可以用向上調整插入的方式去建堆,我們還有另外一種思路:向下調整去建堆
如果我們想要建大堆,能不能直接從2的位置開始向下調呢?
不行~因為向下調整的前提是左右子樹都是大堆,這里明顯不符合。
那如果3的左子樹和右子樹都是大堆是不是意味著可以對3進行向下調整,可惜這兩棵子樹也不是大堆。
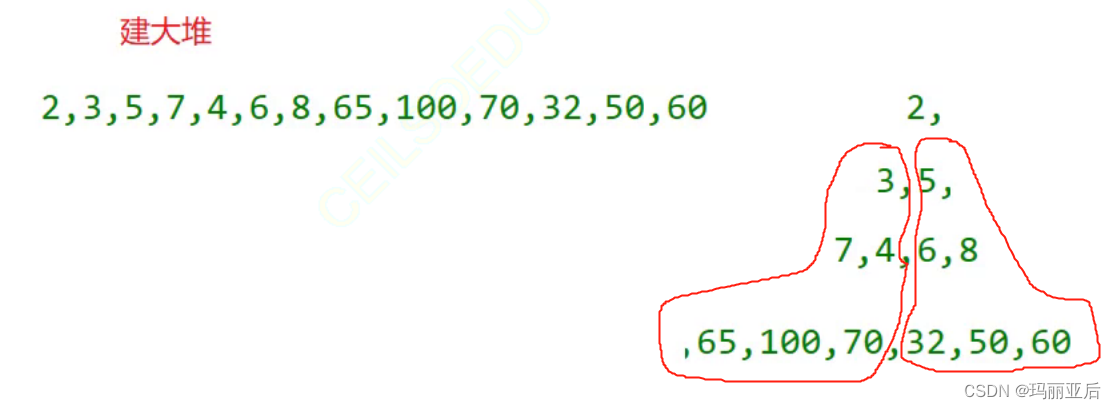
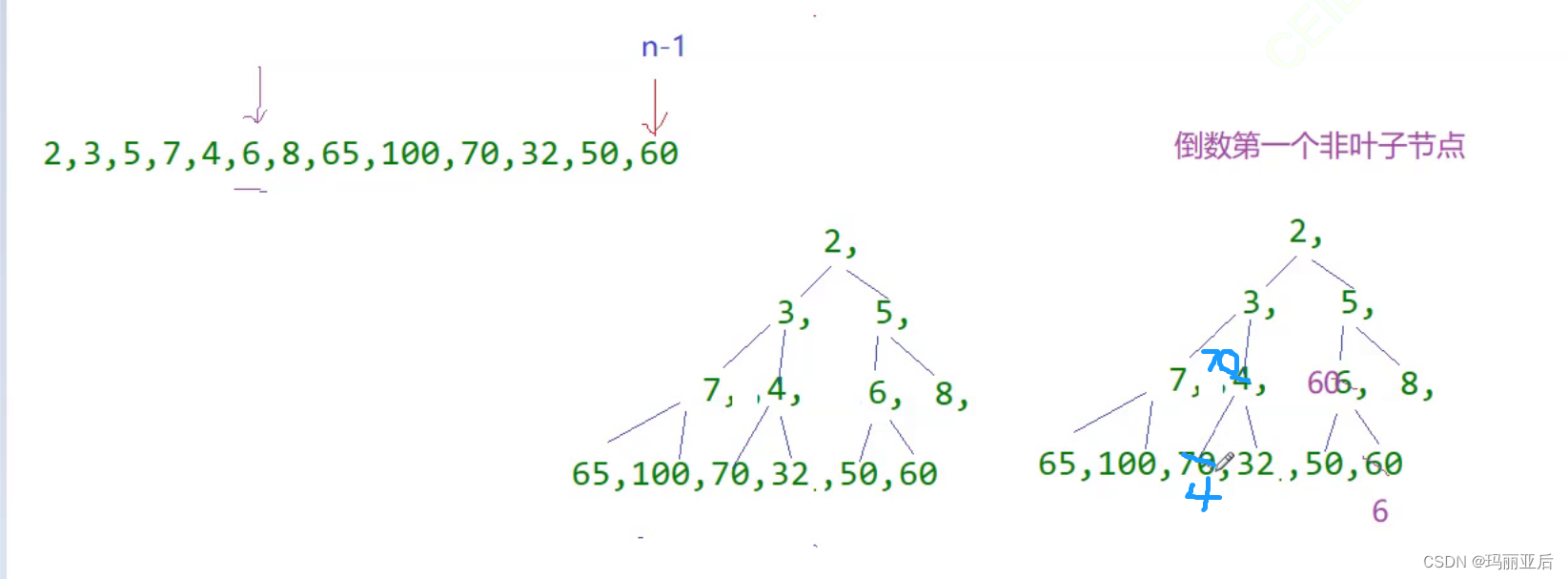
那我們不妨逆向思維——從最底層開始向下調整,從最下面一直調整到最上面,這樣就能保證每一棵左右子樹都是大堆了~不過有一點需要注意,最下面那一行屬于葉子的部分沒必要調整(葉子自己就可以看成大堆)。
所以我們第一個要找的是倒數第一個非葉子節點(6),然后對它進行向下調整(找出最大的孩子——60并和它交換)。
關于它們的下標也很好找尾部60的下標是n-1,那它的父親的下標就是(n-1-1)/2,當我們向下調整好6時,按照順序應該是要調整4這個結點了,而它的下標剛好就在6的前面。以此類推到7這個位置開始調整。
需要找到5的下標跟上面同理,下標--就好了,然后進行向下調整。
最后向下調整結束~
關于代碼部分的實現也很簡單:
void HeapSort(int* a, int n) {//建堆——向上調整建堆//for (int i = 0; i < n; i++)//{// AdjustUp(a, i);//}// //建堆——向下調整建堆for (int i = (n-1-1)/2; i >=0; i--){AdjustDown(a, n, i);}//建大堆升序int end = n - 1;//數組尾部數據下標while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);//選出最大end--;//讓數組最后數據的前一位和堆頂交換} }
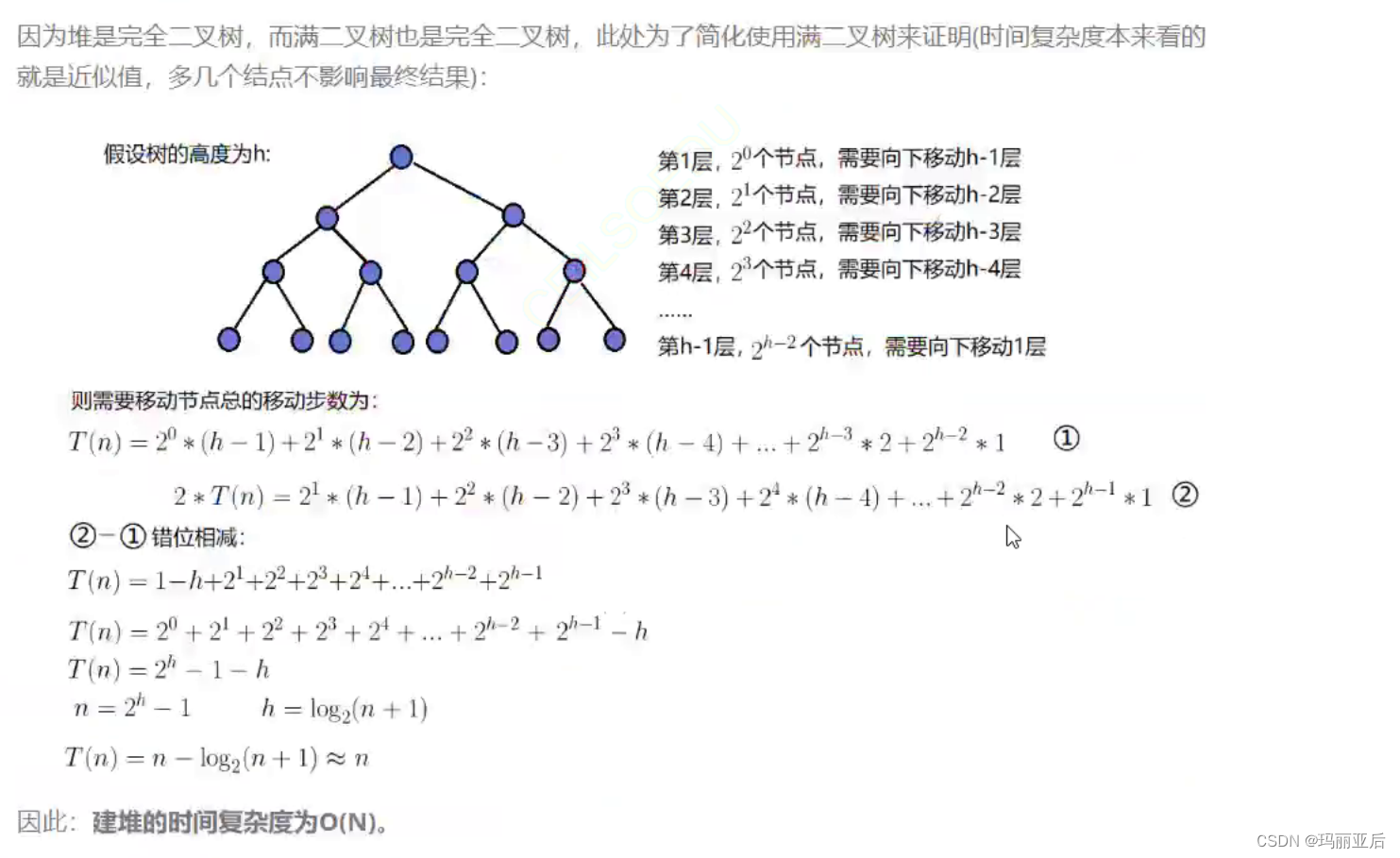
4.3.6.12 建堆復雜度的證明?
?
一般我們更推薦向下調整建堆,因為它效率更高 。
T(h)是一共要調整的次數——倒數第二層調整1次,倒數第三層調整2次.....一直到第一層調整h-1次。
?畫藍框的總和是我們之前數二叉樹節點的個數。
所以向下調整建堆的實際時間復雜度其實要比O(N)小一點點。(因為換算成時間復雜度那得跟N有關,但N又不好表達出來,所以就用h來表達,最后再換成N)
———————————————————————————————————————————
現在我們來用向上調整建堆~
我們會發現相比向下調整法,向上調整的數都是多乘多,最后一個數據是最大的,,換算過來是(N/2)*logN,所以這就是我們為什么會優先選擇向下調整法的原因。
開始錯位相減~
最終向上調整法實際實際復雜度差不多是O(N*logN-N),總而言之,向上調整最后一層數據太多,要調整到上層的層數也多,所以在效率上反而是不如向下調整法的。
這里的堆排序其實可以看作有N個數據在進行向下調整,那結果不言而喻~O(N*logN)
4.3.6.13 小練習(選看)
注:有C語言內存文件基本可放心食用~
假設10億個數據,內存存不下,數據在文件中找出最大的前K個。
基本思路:
- 讀取文件的前100個數據,在內存數組中建立一個小堆
- 再依次讀取剩下數據,跟堆頂數據進行比較,大于堆頂,就替換它進堆,向下調整
- 所以數據讀完,堆里面數據就是最大的前100個
有N個數要遍歷一遍,每一個數最壞情況都要進堆向下調整logK次,當N足夠大時,那時間復雜度就是O(N)了而不是O(N*logK)。空間復雜度——O(K)
void CreateNDate() {//造數據int n = 1000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");//寫操作if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin); }void PrintTopK(const char* filename, int k) {//1. 建堆——用數組a中前k個元素建堆FILE* fout = fopen(filename, "r");//r——讀操作if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);//建立所放堆空間大小if (minheap == NULL){perroe("minheap fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);//把數組數據放入文件中}//開始構建前K個數小堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(minheap, k, i);}//2.將剩余n-k個元素依次與堆頂元素交換,如果比堆頂還小就換下一個//比堆頂大就替換堆頂int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}//上面的操作我們前面寫過了,需要注意的一般是文件那部分代碼別寫錯for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");fclose(fout); }int main() {CreateNDate();PrintTopK("Data.txt", 10);return 0; }
為了驗證是否真的找到了10個最大的數,我們先預先寫好10個比一百萬還大的數字,到時候看看是否可以找到它們——其他數都比一百萬小,直接在文件里手動插入比100萬大的數,不經歷取模看能不能找到。
成功實現~
五.全部代碼
//Heap.h #pragma once #include <stdio.h> #include <assert.h> #include <stdlib.h> #include <stdbool.h> #include <string.h> #include <time.h> typedef int HPDataType; typedef struct Heap {HPDataType* a;int size;int capacity; }HP;//初始化函數 void HeapInit(HP* php);//另一種初始化函數 void HeapInitArray(HP* php, int* a, int n);//銷毀函數 void HeapDestroy(HP* php);//插入函數 void HeapPush(HP* php, HPDataType x);//交換函數 void Swap(HPDataType* p1, HPDataType* p2);//打印函數 void HeapPrint(HP* php);//向上調整函數 void AdjustUp(HPDataType* a, int child);//刪除函數 void HeapPop(HP* php);//獲取根值函數 HeapTop(HP* php);//向下調整函數 void AdjustDown(HPDataType* a, int n, int parent);//判空函數 bool HeapEmpty(HP* php);————————————————————————————————————————
//Heap.c #include "Heap.h"//初始化函數 void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0;}//另一種初始化函數 void HeapInitArray(HP* php, int* a, int n) {assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}php->size = 0;php->capacity = 0;memcpy(php->a, a, sizeof(HPDataType) * n);for (int i = 1; i < n; i++){AdjustUp(php->a, i);} }//銷毀函數 void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0; }//交換函數 void Swap(HPDataType* p1, HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp; }//向上調整函數 void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;//再用公式去算父親的下標來找到父親while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}} }//插入函數 void HeapPush(HP* php, HPDataType x) {assert(php);//擴容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);//不僅要把數組傳過去,我們還得把孩子也傳過去,而孩子可以通過下標找到 }//打印函數 void HeapPrint(HP* php) {assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");}//向下調整函數 void AdjustDown(HPDataType* a, int n, int parent) {//假設左右孩子中小的為左孩子int child = parent * 2 + 1;while (child < n)//換到葉子就終止,循環結束后child已經是指向數組外了{//找出小的孩子if (child + 1 < n && a[child + 1] < a[child])//如果右孩子比左孩子小{child++;//小的孩子變成右孩子}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//繼續向下調整parent = child;child = parent * 2 + 1;//跟向上調整法一樣,交換完后把parent和child都移下一層為下一次的循環作準備}else{break;}} }//刪除函數 void HeapPop(HP* php) {assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//刪除數據AdjustDown(php->a, php->size, 0); }//獲取根值函數 HeapTop(HP* php) {assert(php);assert(php->size > 0);return php->a[0]; }//判空函數 bool HeapEmpty(HP* php) {assert(php);return php->size == 0; }————————————————————————————————————————
//Test.c #include "Heap.h"樹的最優設計 //struct TreeNode //{ // int val; // struct TreeNode* firstchild; // struct TreeNode* nextbrother; //}; // //void HeapSort(int* a, int n) //{ // HP hp; // HeapInit(&hp); // for (size_t i = 0; i < sizeof(a) / sizeof(int); i++) // { // HeapPush(&hp, a[i]); // } // int i = 0; // // while (!HeapEmpty(&hp)) // { // //printf("%d ", HeapTop(&hp)); // a[i++] = HeapTop(&hp); // HeapPop(&hp); // // } // // // HeapDestroy(&hp); //}//void HeapSort(int* a, int n) //{ // //建堆 // for (int i = 0; i < n; i++) // { // AdjustUp(a, i); // } // //建大堆升序 // int end = n - 1;//數組尾部數據下標 // while (end > 0) // { // Swap(&a[0], &a[end]); // AdjustDown(a, end, 0);//選出最大 // end--;//讓數組最后數據的前一位和堆頂交換 // } //}void HeapSort(int* a, int n) {//建堆——向上調整建堆//for (int i = 0; i < n; i++)//{// AdjustUp(a, i);//}// //建堆——向下調整建堆for (int i = (n-1-1)/2; i >=0; i--){AdjustDown(a, n, i);}//建大堆升序int end = n - 1;//數組尾部數據下標while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);//選出最大end--;//讓數組最后數據的前一位和堆頂交換} }//int main() //{ // //int a[] = { 65, 100, 70, 32, 50, 60 }; // int a[] = { 70, 65, 100, 32, 50, 60 }; // HeapSort(a, sizeof(a) / sizeof(int)); // // return 0; //} void CreateNDate() {//造數據int n = 1000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");//寫操作if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin); }void PrintTopK(const char* filename, int k) {//1. 建堆——用數組a中前k個元素建堆FILE* fout = fopen(filename, "r");//r——讀操作if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);//建立所放堆空間大小if (minheap == NULL){perroe("minheap fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);//把數組數據放入文件中}//開始構建前K個數小堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(minheap, k, i);}//2.將剩余n-k個元素依次與堆頂元素交換,如果比堆頂還小就換下一個//比堆頂大就替換堆頂int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}//上面的操作我們前面寫過了,需要注意的一般是文件那部分代碼別寫錯for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");fclose(fout); }int main() {CreateNDate();PrintTopK("Data.txt", 10);return 0; }
 六.結語
六.結語
本文除了給友友們普及二叉樹與堆的概念外,更重要的是關于堆功能的代碼實現,其中的方法會幫助提高我們的算法效率。最后感謝大家的觀看,友友們能夠學習到新的知識是額滴榮幸,期待我們下次相見~






























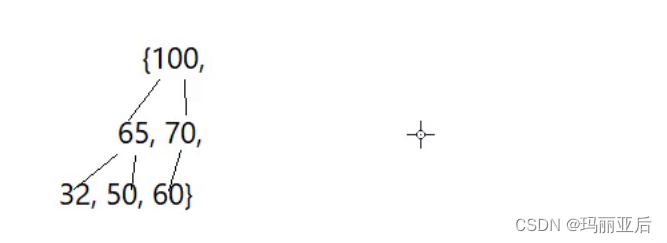

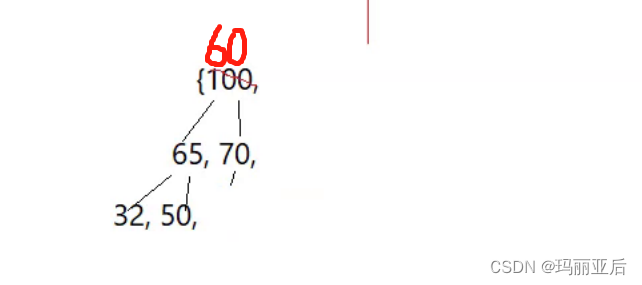













)



#困難,想不到)






)







