一、122.買賣股票的最佳時機 II

力扣題目鏈接

🦄解題思路：

首先需要明確的幾個點：

• 當前只能有最大一支股票
• 每一天操作只能3選1：買or賣or休息

此外，對于貪心，總有像下面圖示的一種直覺：如果后一天比今天高，則買，否則不買；這是正確的直覺：

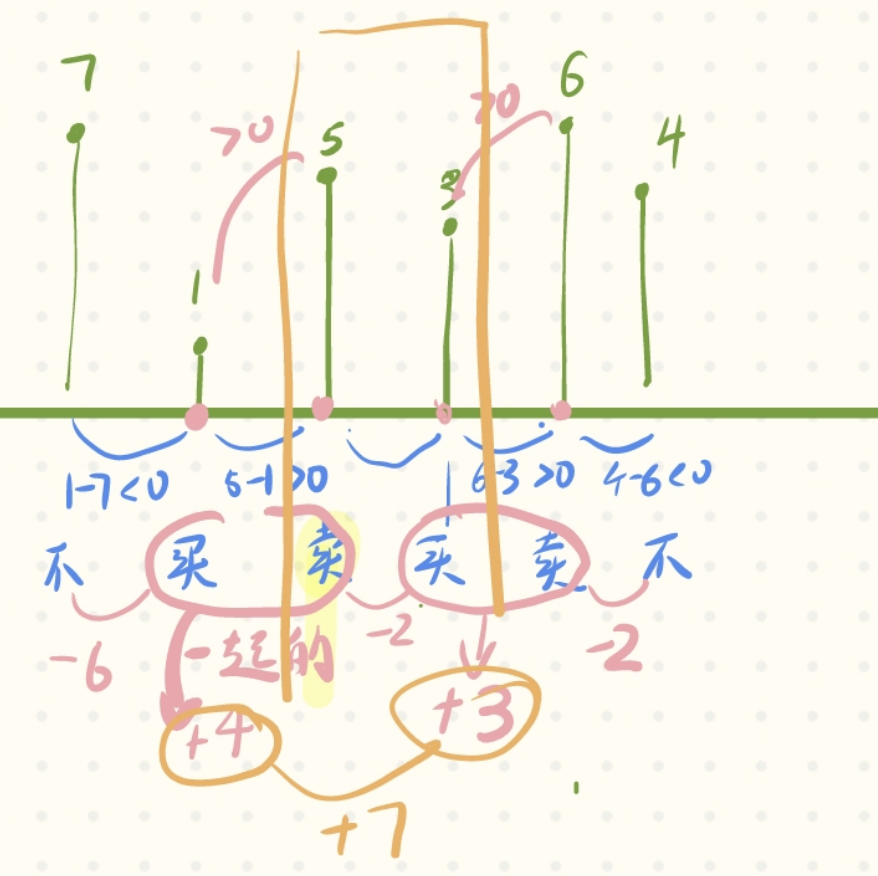
那么這里可能想給出這樣的一個思路：

• 若當前元素的價格低于后面元素，則買入，并在后面一個元素賣出：相當于：確定了，今天買，必須明天賣；如此遍歷。
• 若當前元素的價格高于后面元素，則當前元素不動，即休息一天。

沒錯，很有道理，但是我想到了一個反例：
如下圖，如果按照上面的思路，則第一個元素買入，第二個元素賣出；遍歷到第二個元素時，由于已經賣出，按理來說不能再操作了，但是由于當前元素低于第三個元素，還應該買下第二個元素，這樣似乎違法了每天只能有一個操作的前提。

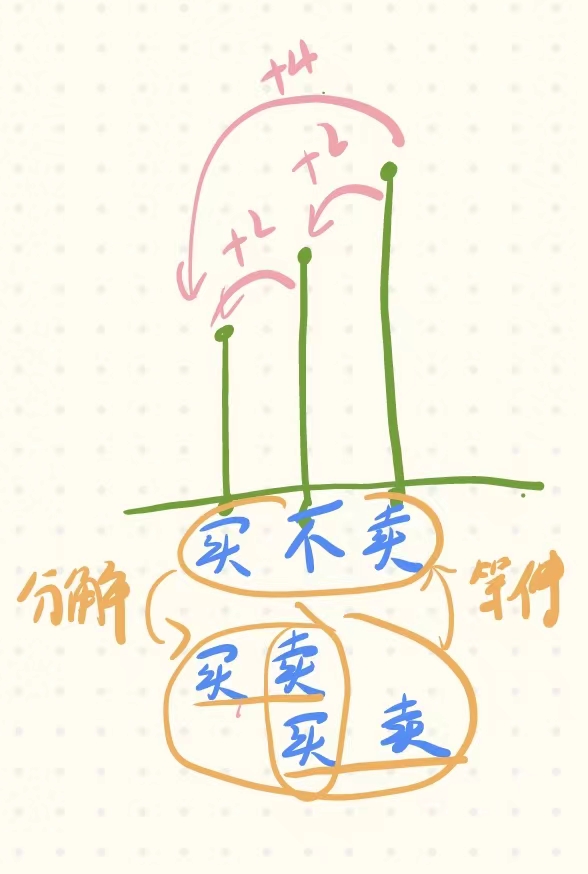
但是后來看了一些題解，發現這種情況根本不影響，雖然正確情況的：第 0 天買入，第 2 天賣出，那么利潤為：prices[2] - prices[0]。相當于 (prices[2] - prices[1]) + (prices[1] - prices[0])。也正是由于這種情況,也就是說，計算過程并不等同于實際交易過程，但是計算買賣利潤的總和的結果(prices[2] - prices[1]) + (prices[1] - prices[0])，和實際交易情況prices[2] - prices[0]的結果一致，這也是為什么可以這么算！

而且還要發現一點的是，買和賣總是一個單位，它們之間可能有“休息”，像上圖一樣，但是分解過后，還是兩天“買”和“賣”為一個單元。只有這樣才能獲得最大利潤。

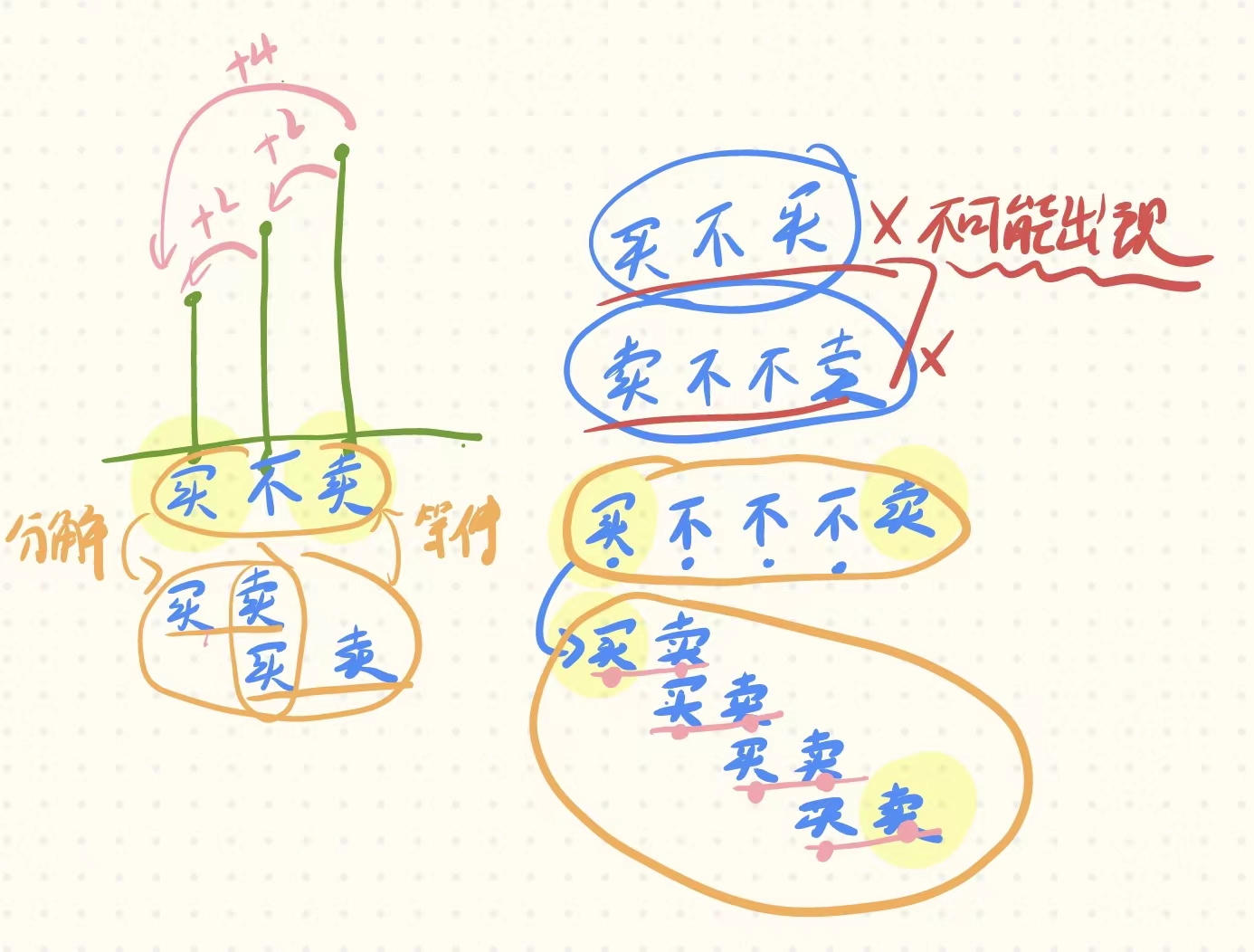
所以這題還是一個比較偏直覺的，一開始可能會像我一樣，死磕在當前這一天的操作上（一天操作只能三選一），從而無法下手。

所以具體算法過程如下，貪心貪的就是收集所有正項：

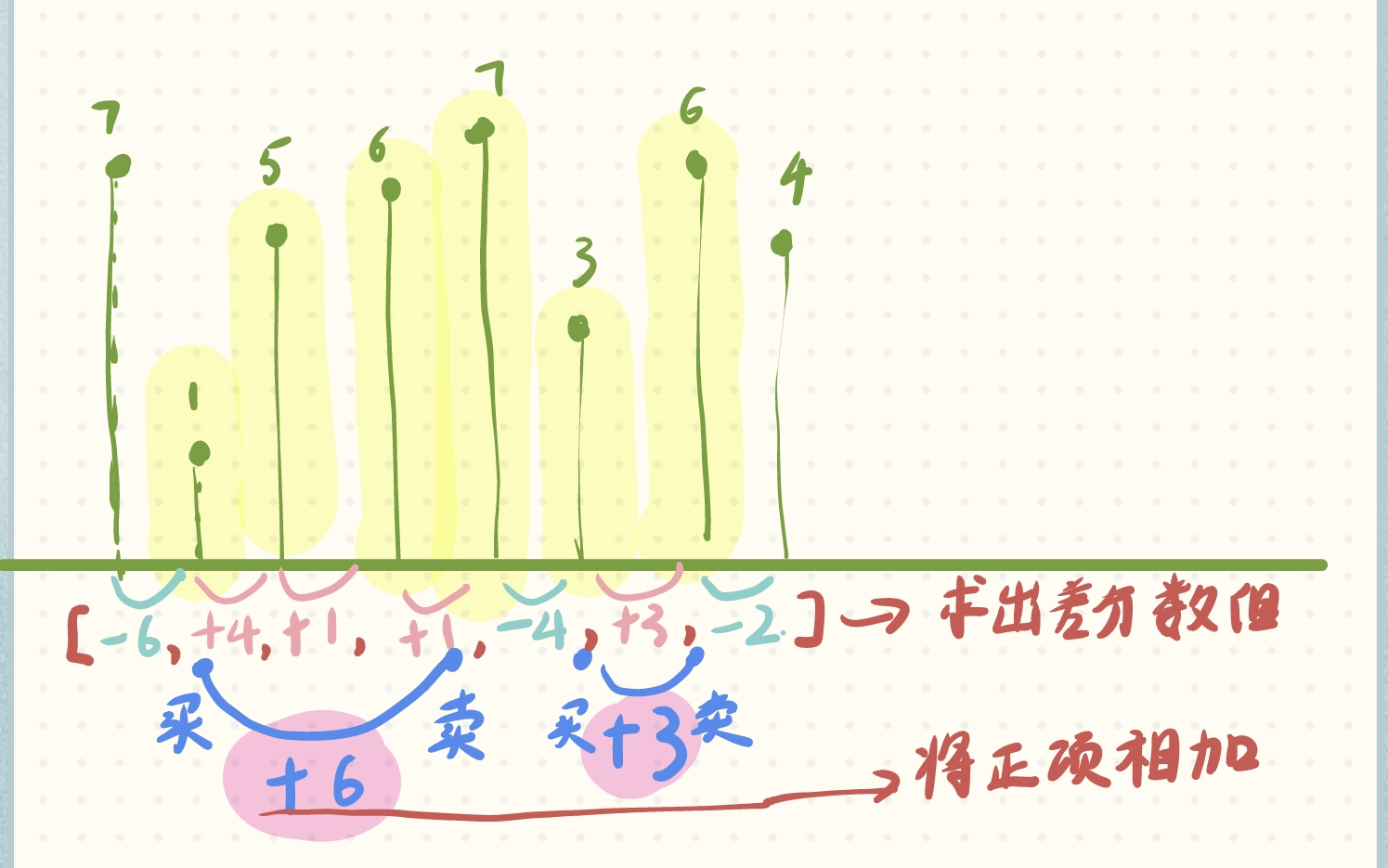
貪心算法和動態規劃相比，它既不看前面（也就是說它不需要從前面的狀態轉移過來），也不看后面（無后效性，后面的選擇不會對前面的選擇有影響），因此貪心算法時間復雜度一般是線性的，空間復雜度是常數級別的；

?正確代碼：

class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for (int i = 1; i < prices.size(); i++){res += max(prices[i]-prices[i-1],0);}return res;}
};

二、55. 跳躍游戲

力扣題目鏈接

🦄解題思路：

我個人在做這題時并沒有做出來，而是陷入了兩個思維誤區：

• 總是在想，比如當前位于元素值為3的位置，我是走1步還是走2步呢？還是3步呢？
• 好像有點像動態規劃的跳樓梯？但是似乎不能從后往前推？狀態方程很難確定

其實這題還是貪心，而且它根本不拘泥與到底跳多少步，而是你能跳到哪？或者說你最遠能跳到哪里！你跳躍的覆蓋范圍！為什么這么說呢，可以看下面的圖解：

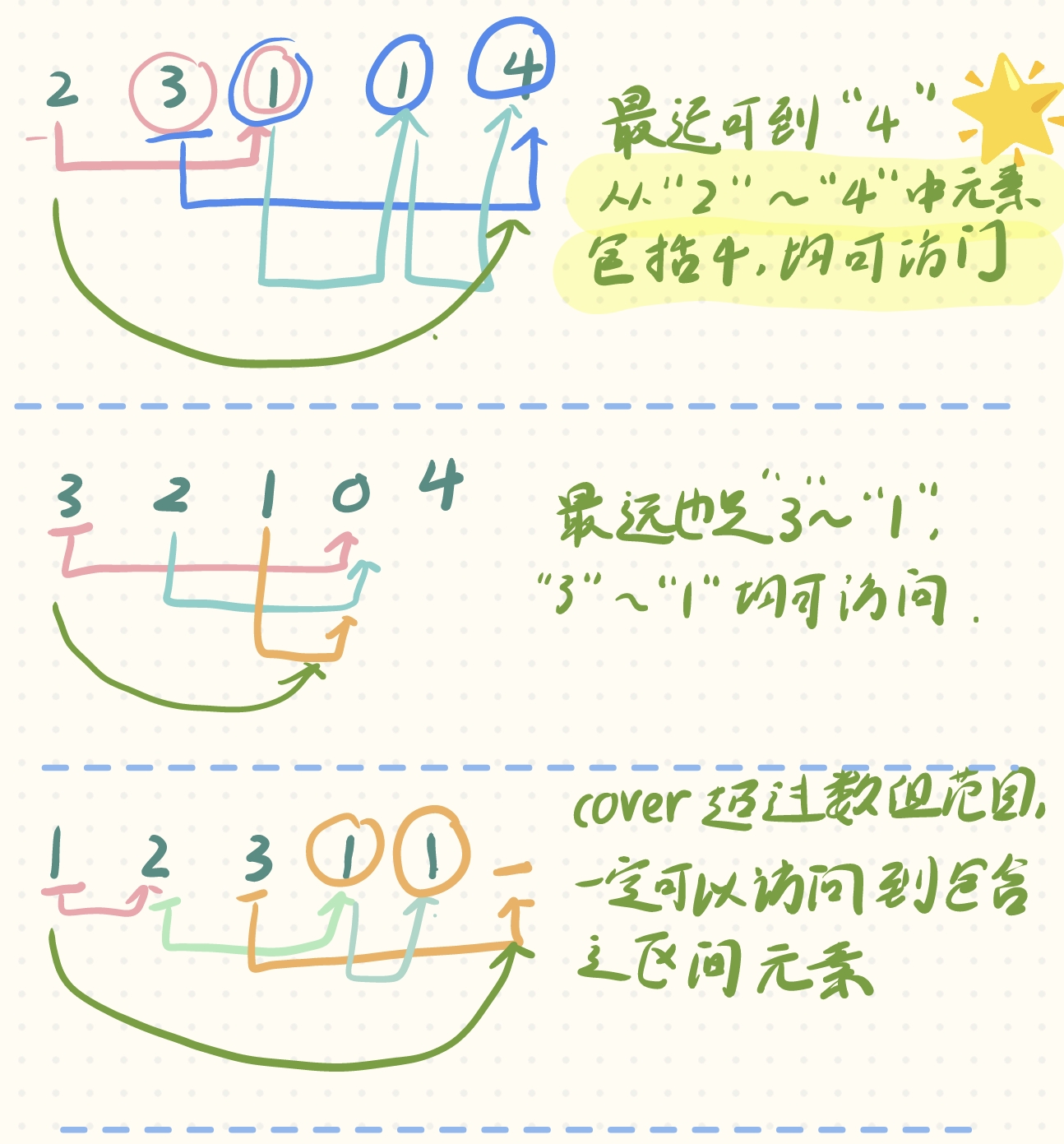
所以這題的coding核心如下

• cover變量，實時記錄和更新當前cover的最遠距離
• for循環逐個遍歷數組元素，更新cover（注意for循環的邊界

?錯誤代碼和分析1：

class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示當前覆蓋長度for (int i = 0; i < nums.size() - 1; i++){cover = max(i+1+nums[i],cover);}return cover >= nums.size()? true : false;}
};

• 沒有考慮只有一個元素：
  

?錯誤代碼和分析2：

class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示當前覆蓋長度if (nums.size() == 1) return true; // 只有一個元素，就是能達到for (int i = 0; i < nums.size() - 1; i++){cover = max(i+1+nums[i],cover);}return cover >= nums.size()? true : false;}
};

• for循環邊界不是nums.size()-1而是cover!指到這個元素，確定范圍cover，起碼你要能到這個元素吧。遍歷都是要遍歷能到達的元素（也就是cover內的，即使cover是隨時更新的）。比如這個第一個元素是0，那么你都到不了第二個元素；
  

?正確代碼：

class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示當前覆蓋數組范圍if (nums.size() == 1) return true; // 只有一個元素，就是能達到for (int i = 0; i <= cover; i++){cover = max(i + nums[i],cover);if (cover >= nums.size()-1) return true; // 說明可以覆蓋到終點了}return false;}
};