腦電信號一直伴隨著人類的生命，腦電波是腦神經細胞發生新陳代謝、離子交換時細胞群興奮突觸電位總和，腦電信號的節律性則和丘腦相關，含有豐富的大腦活動信息。通常我們所接觸的腦電圖都是頭皮腦電圖，在有些特殊場合還需要皮下部位的腦電圖，腦電信號主要有以下幾個特點：

（1）腦電信號只有50pV左右，所以非常的微弱，通常頭皮腦電信號，超過100pV的可以認作是噪聲。腦電信號按照波幅值可以分為高、中、低三種:低波幅值小于25pV；中波幅值大于25pV小于50pV；高波幅值大于50pV。

（2）具有隨機性及非平穩性。腦電信號被影響的因素很多，但規律通常都沒有被識別，通常來說，腦電信號的規律從大量的數據統計、大量的技術處理檢測、識別和估計結果中顯示，并且生命體對外界的自適應力，以及生理因素的作用都對腦電信號產生了影響，所以腦電信號具有著隨機性和非平穩性，并且一直隨著時間在變化。

（3）具有非高斯、非線性的特征。生物組織自適應和生理機使得人體腦電的信號有非線性的特性，當前信號處理通常通過線性系統分析基礎上進行，所以在分析方法上如何最小地去減小非線性誤差在腦電信號的處理上也應該要考慮。

（4）腦電信號容易受到諸多的背景噪聲干擾。影響腦電波的因素還有很多。比如人的年齡，當人在50歲以后，慢波又可以逐漸回升，還有著不同程度的基頻慢波。腦波還更易受到意識、情緒以及思維狀態等因素的影響。

腦電波在病理的狀態下的形態也經常會出現一些異常瞬態波。尖波周期范圍是在80~200ms，其波形快速上升、緩慢下降，類似于三角波，病癥常見于癲癇。棘波多見于局限性的癲癇，而棘慢綜合波是通過棘波和慢波所構成的復合波。

鑒于此，本項目采用譜分析方法，對兩個來源（PhysioNet數據庫和自測數據庫）的腦電信號進行了研究，目標是應用不同的時頻譜分析技術評估相應的結果。算法程序運行環境為MATLAB R2021b，執行EEG信號的譜分析，也可遷移至金融時間序列，地震信號，機械振動信號，語音信號，聲信號等一維時間序列信號。

部分代碼如下：

%EEG Signal Spectral Analysis
%Load data & Initialize params
%Sleep dataset
clear;
[x, Fs, Start_date, Start_time, Label, Dimension, Coef, Nmb_chans,N] = readedf_EX1('sc4002e0.rec',0,0,360);
windows = int16([128 256 512]);
overlaps = double([0 0.25 0.50 0.75]);
dft_points = [64 128 256 512 1024];
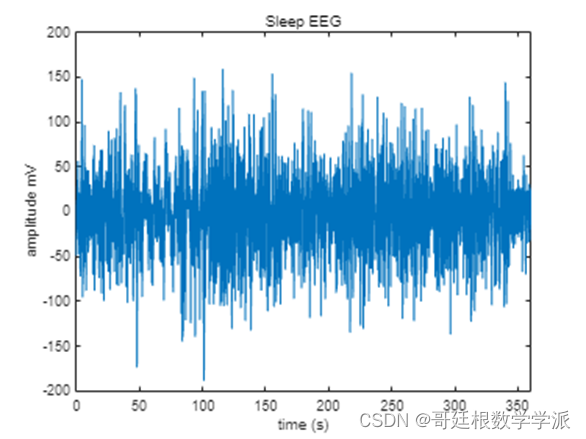
Signal overview
figure
time = linspace(0,length(x)/Fs, length(x));
plot(time,x)
axis('normal')
title('Sleep EEG')
xlim([0 length(time)/Fs])
xlabel('time (s)')
ylabel('amplitude mV')1. PSD params experiment1.1 Window size
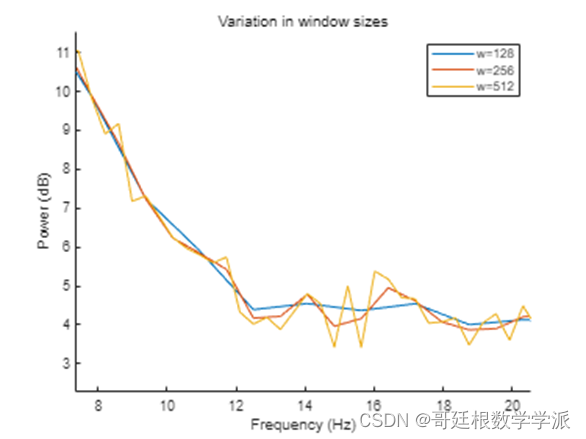
figure
hold on
for i=1:length(windows)[pxx, f] = pwelch(x,windows(i),overlaps(3)*windows(i),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('w=%d', windows(1)), ...sprintf('w=%d',windows(2)), ...sprintf('w=%d', windows(3)))
xlabel('')
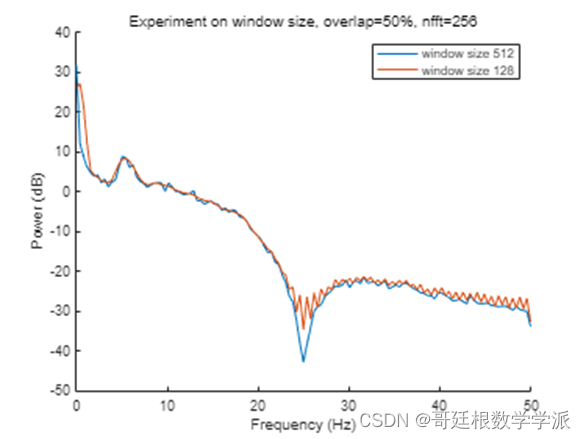
title('Variation in window sizes')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off
% Better visualization for comparision
xlim([7.37 20.53])
ylim([2.30 11.52])1.2 Overlap
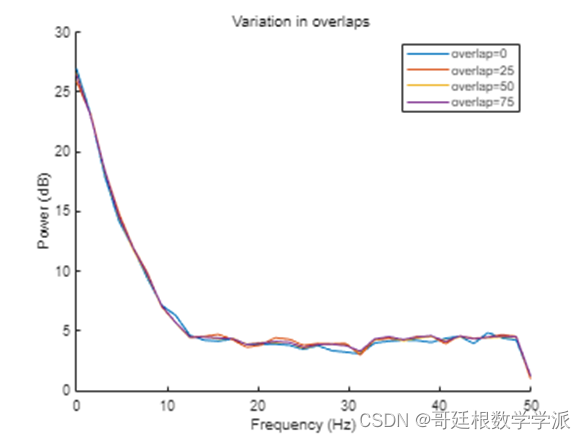
figure
hold on
noverlaps = overlaps .* 128;
for i=1:length(noverlaps)[pxx, f] = pwelch(x, windows(1), noverlaps(floor(i)), dft_points(1), 100);plot(f, pow2db(pxx),'LineWidth',1)
end
legend(sprintf('overlap=%d %', overlaps(1)*100), ...sprintf('overlap=%d %', overlaps(2)*100), ...sprintf('overlap=%d %', overlaps(3)*100),...sprintf('overlap=%d %', overlaps(4)*100))
xlabel('')
title('Variation in overlaps ')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off1.3 Number of DFT points
figure
hold on
for i=1:length(dft_points)[pxx, f] = pwelch(x,windows(1),overlaps(2)*windows(1),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('nfft=%d', dft_points(1)), ...sprintf('nfft=%d',dft_points(2)), ...sprintf('nfft=%d',dft_points(3)), ...sprintf('nfft=%d',dft_points(4)), ...sprintf('nfft=%d', dft_points(5)))
xlabel('')
title('Variation in number of DFT points')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off2. Spectrogram params experimentspec_w_1 = 128;
spec_w_2 = 512;
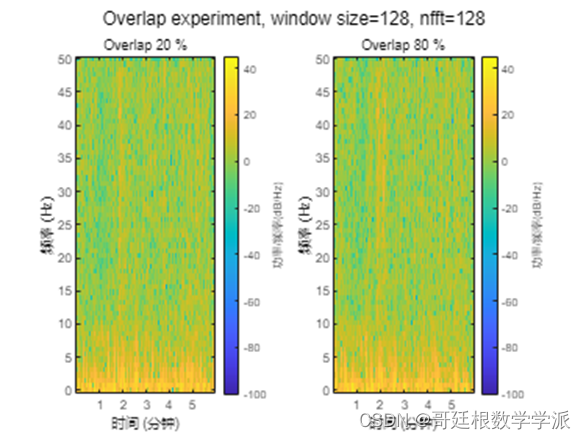
spec_o_1 = 0.5;
spec_o_2 = 0.8;
spec_o_3 = 0.2;
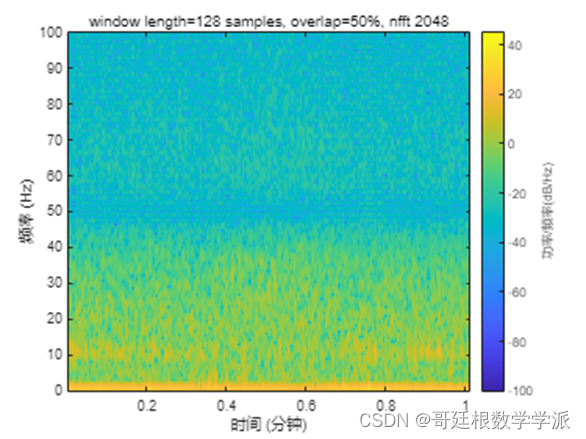
spec_nfft_1 = 128;
spec_nfft_2 = 1024;2.1 Window size
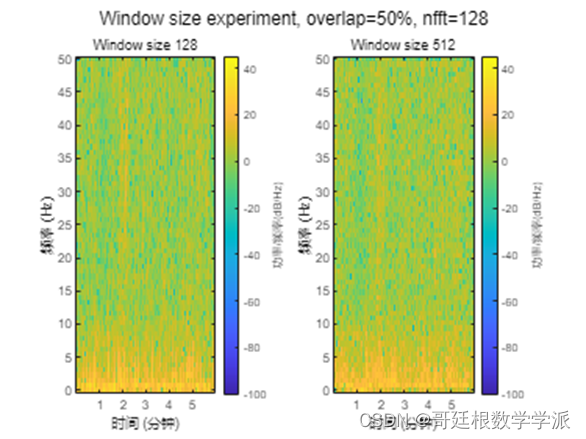
Small window size results in high detail frequecy representation.
Large window size results in blocky-looking frequecy representation.
figure;
subplot(1,2,1);
spectrogram(x,spec_w_1,64,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_1))subplot(1,2,2);
spectrogram(x,spec_w_2, spec_o_1 * spec_w_2,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_2))sgtitle(sprintf('Window size experiment, overlap=%d%%, nfft=%d', spec_o_1*100, spec_nfft_1));

出圖如下：

工學博士，擔任《Mechanical System and Signal Processing》審稿專家，擔任
《中國電機工程學報》優秀審稿專家，《控制與決策》，《系統工程與電子技術》，《電力系統保護與控制》，《宇航學報》等EI期刊審稿專家。

擅長領域：現代信號處理，機器學習，深度學習，數字孿生，時間序列分析，設備缺陷檢測、設備異常檢測、設備智能故障診斷與健康管理PHM等。