𝙉𝙞𝙘𝙚!!👏🏻???????👏🏻??????? 👏🏻?????:Solitary_walk

? ? ? ?? ? ━━━┓
? ? ?- 個性標簽 - ：來于“云”的“羽球人”。 Talk is cheap. Show me the code
┗━━━━━━━ ?? ?

本人座右銘 ： ? 欲達高峰,必忍其痛;欲戴王冠,必承其重。

👑💎💎👑💎💎👑?
💎💎💎自💎💎💎
💎💎💎信💎💎💎
👑💎💎　💎💎👑 ? ?希望在看完我的此篇博客后可以對你有幫助喲

👑👑💎💎💎👑👑 ? 此外，希望各位大佬們在看完后，可以互相支持，蟹蟹！
👑👑👑💎👑👑👑

---

對二叉樹的基本概念性的理解，若有不明白的友友們，可以看一下前期寫的關于堆與二叉樹的精講

鏈接在此：

有了大家對二叉樹的基本理解接下來，對以下知識的理解應該是易如反掌！

1.二叉樹的鏈式結構的實現

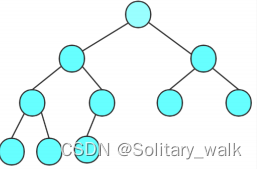
?對于任何一個二叉樹的節點來說：都是由值域，左孩子，右孩子構成，只不過對于某些節點而言左右孩子為空

1.1定義一個二叉樹的結構體

typedef int BT_DataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left; //左孩子struct BinaryTreeNode* right;//右孩子BT_DataType val;  //值域}BT;

1.2二叉樹的鏈式結構

?為了方便對二叉樹的理解，我暫時手動創建節點，進行連接

BT* BT_Create()
{BT* n1 = BuyNode( 1);BT* n2 = BuyNode( 2);BT* n3 = BuyNode( 3);BT* n4 = BuyNode( 4);BT* n5 = BuyNode(5);BT* n6 = BuyNode( 6);BT* n7 = BuyNode( 7);BT* n8= BuyNode( 8);BT* n9 = BuyNode( 9);BT* n10 = BuyNode( 10);n1->left = n2;n1->right = n3;n2->right = n4;n3->left = n5;n3->right = n6;n2->left = n7;n4->left = n8;return n1;
}

2.二叉樹的遍歷

2.1前序遍歷（先序遍歷）

先訪問根節點，其次訪問左子樹，左后訪問右子樹，注意這是一個遞歸的定義。

見圖如下：

?代碼：

void Pre_order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示為空return;}printf("%d ", root->val);Pre_order(root->left);Pre_order(root->right);
}

遞歸展開圖的解釋：

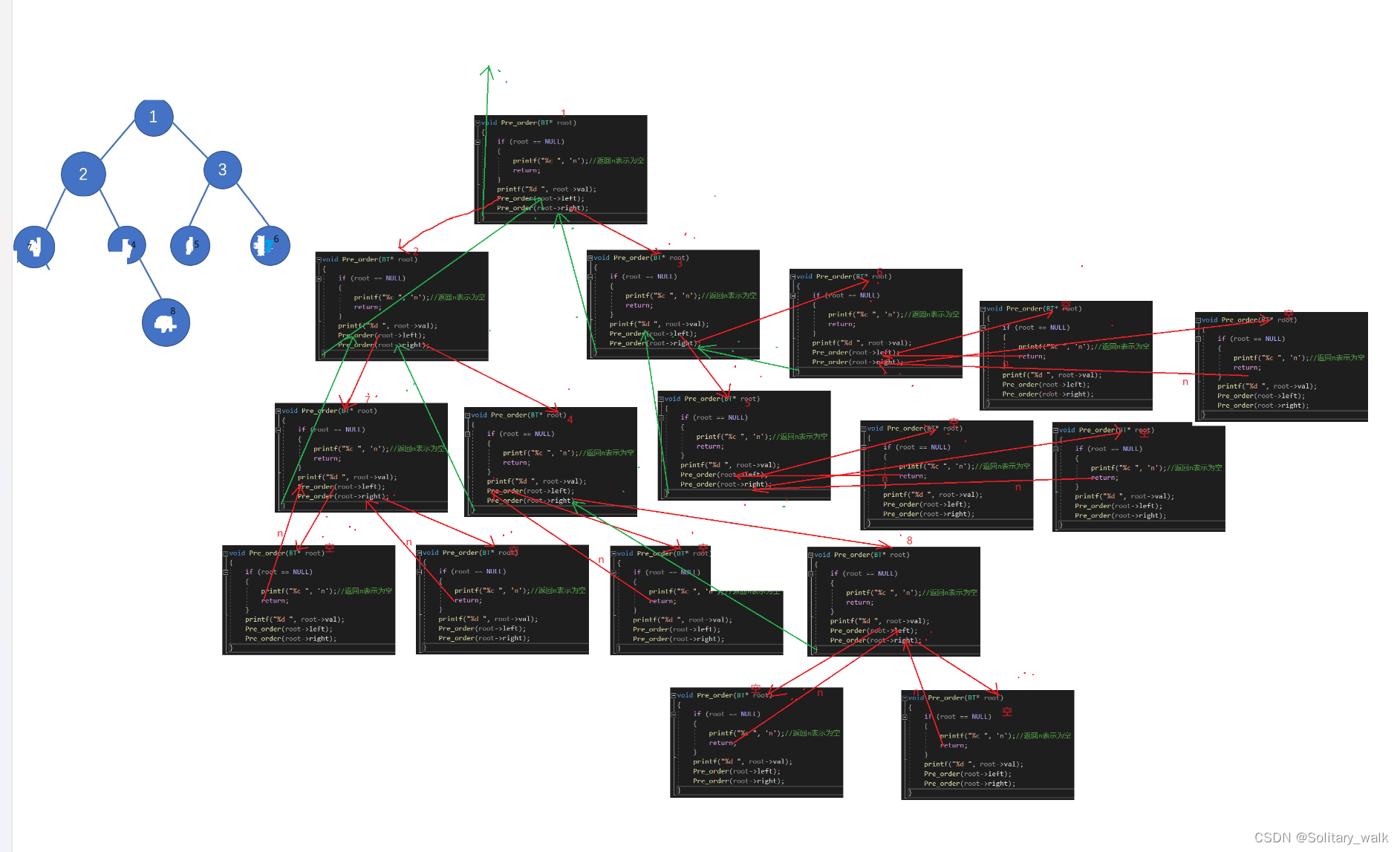
2.2中序遍歷

先訪問左子樹，在訪問根節點最后訪問右子樹，依然是一個遞歸的定義

分析如下：

?代碼：

void In_Order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示為空return;}In_Order(root->left);printf("%d ", root->val);In_Order(root->right);
}

2.3后續遍歷

先訪問左子樹，再訪問右子樹，最后訪問根節點，依然是遞歸定義

分析見下：

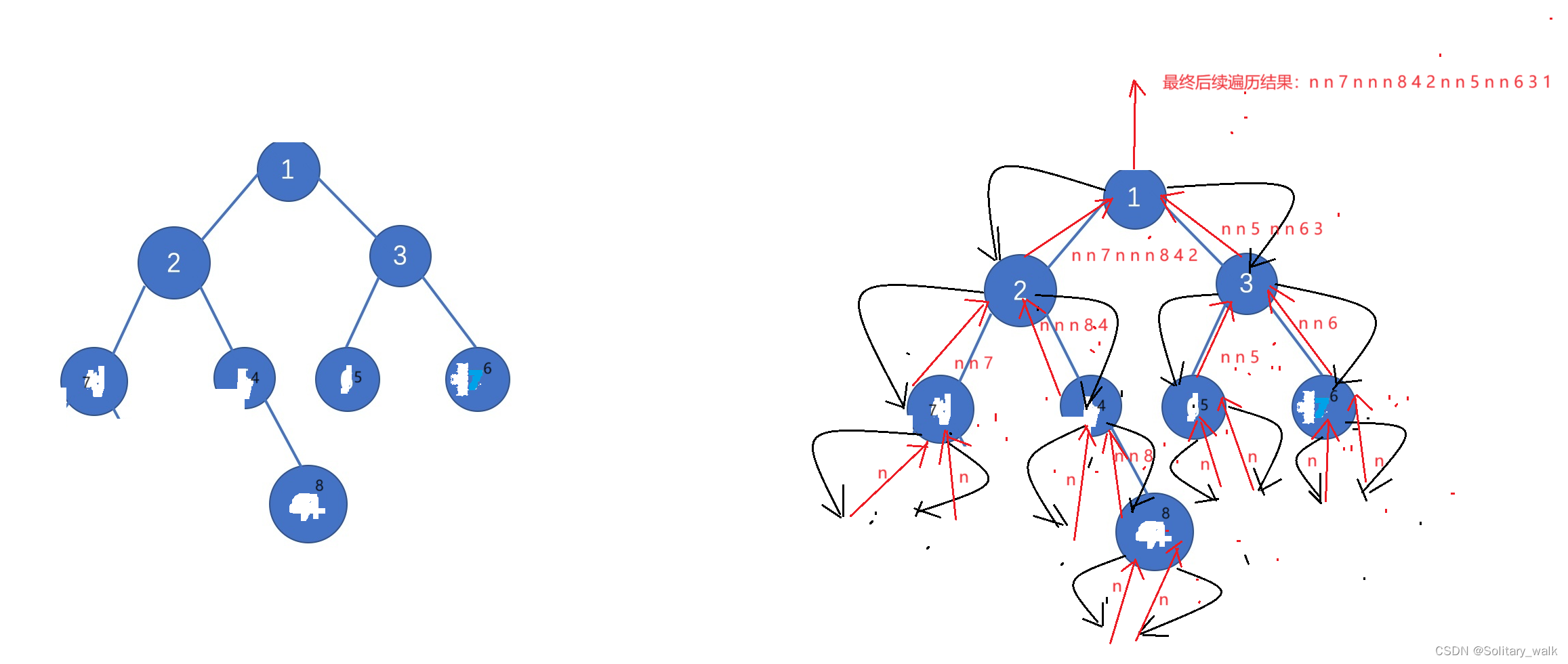
代碼：

void Post_Order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示為空return;}Post_Order(root->left);Post_Order(root->right);printf("%d ", root->val);}

3.與二叉樹相關節點的求解

3.1求二叉樹所有節點個數

可能有些老鐵們會說：直接進行計數就可以了：只有是當前節點不為空就讓計數器（size）加一，采用前序遍歷的方法。沒錯也可以這樣但是這樣有些坑需要注意一下否則一不小心就掉進坑里了。

?

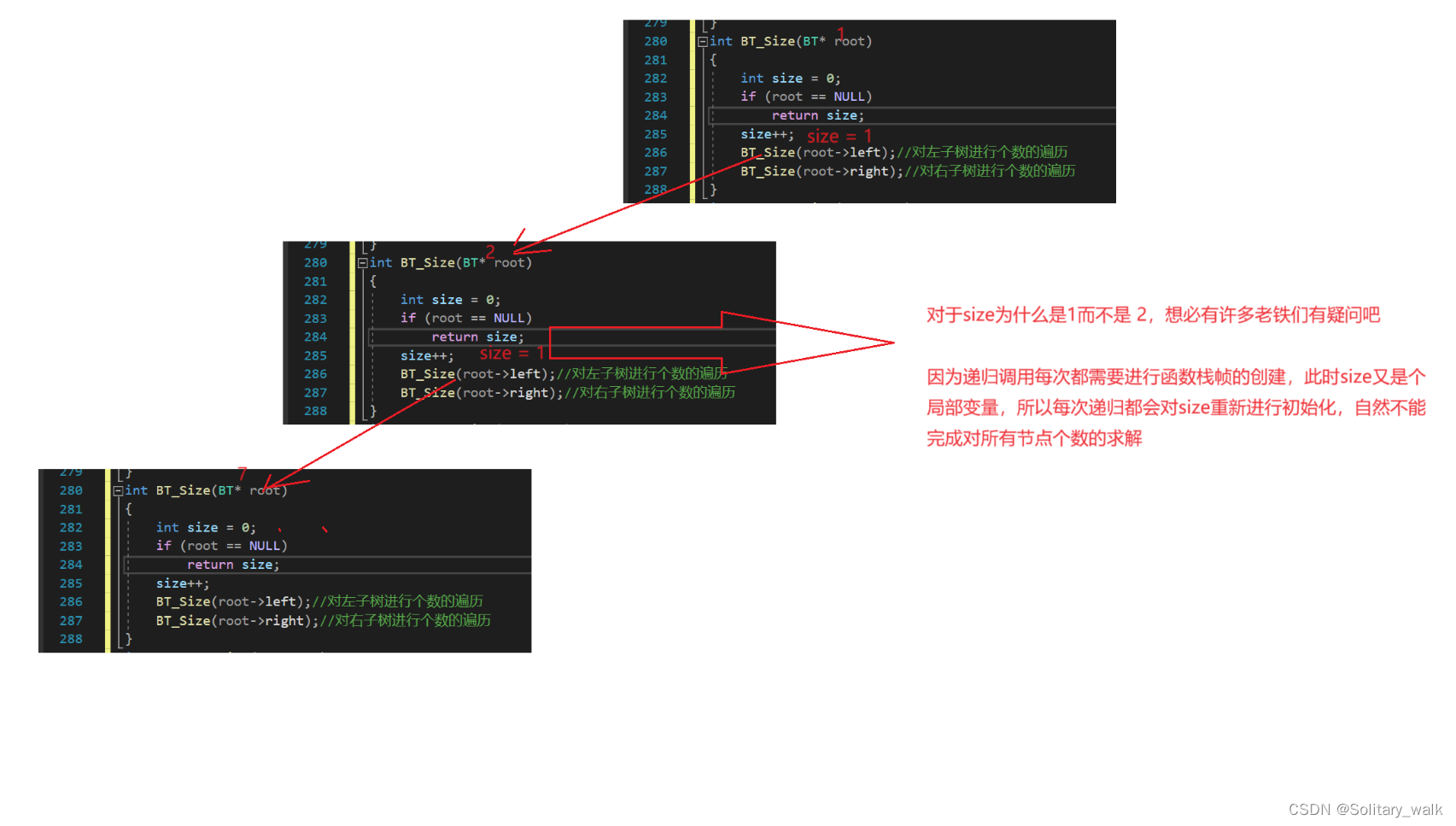
?這時候可能有老鐵會說，直接定義一個全局變量不就OK了，注意當我們連續調用BT_Size()這個函數進行求個數的話會有問題滴！

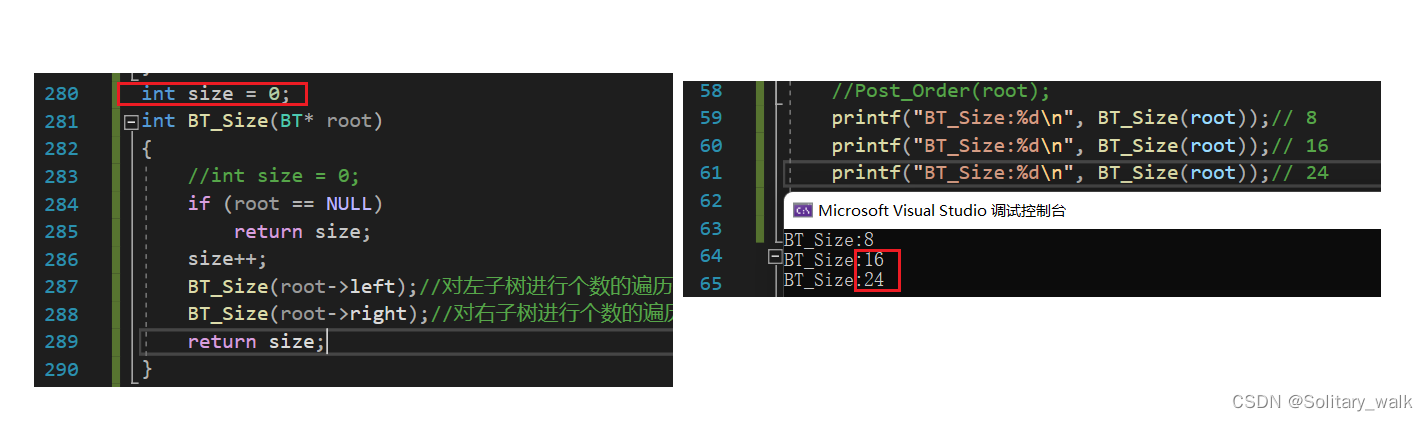
?因為szie作為一個全局變量，第一調用確實為8沒有錯，但是當我們后續在進行調用的時候就需要把size 手動進行置零，（關于這個問題詳解，感興趣的友友們，可以看前期我寫的博客：鏈接在此，自取，蟹蟹支持!）要不然只會在當前size = 8 的基礎上進行相加，這也就是為什么最后會出現16,24的這樣結果了，也就不以為奇了。

代碼：

int size = 0;
int BT_Size(BT* root)
{//int size = 0;if (root == NULL)return size;size++;BT_Size(root->left);//對左子樹進行個數的遍歷BT_Size(root->right);//對右子樹進行個數的遍歷return size;
}

?運行結果：

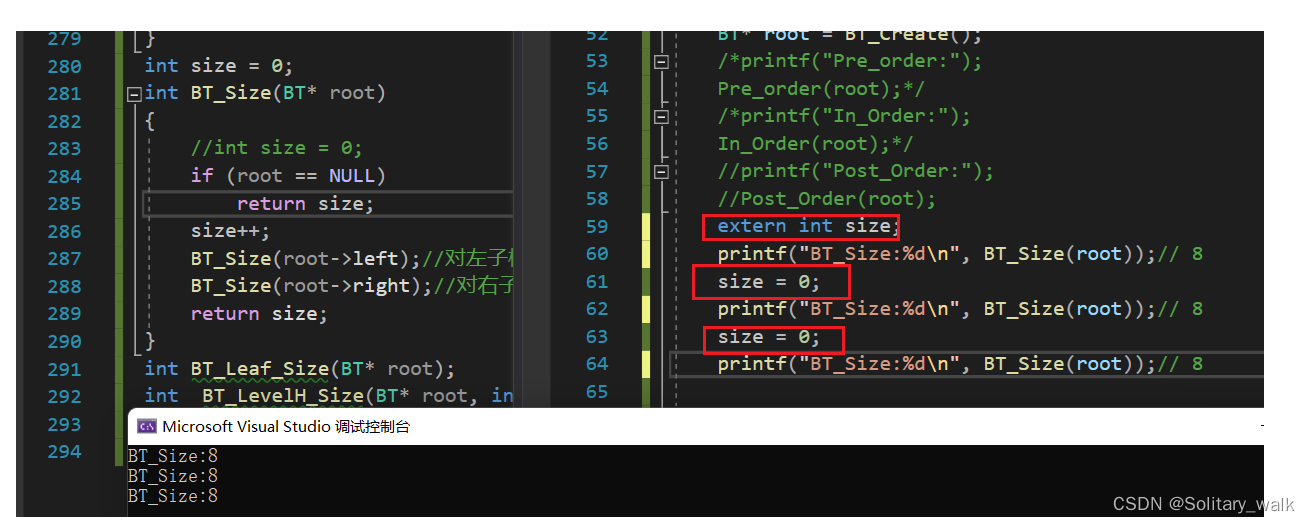
3.2求二叉樹葉節點個數

既然是讓咱求葉節點個數，咱就需要知道什么是葉節點：度為0的節點（沒有左孩子，也沒有右孩子的節點）

通過前面對二叉樹的遍歷咱們應該漸漸對遞歸要有些體悟了，當一個問題很大的時候，可以化大為小，化繁為簡。這樣豈不是很爽！

?分析見下：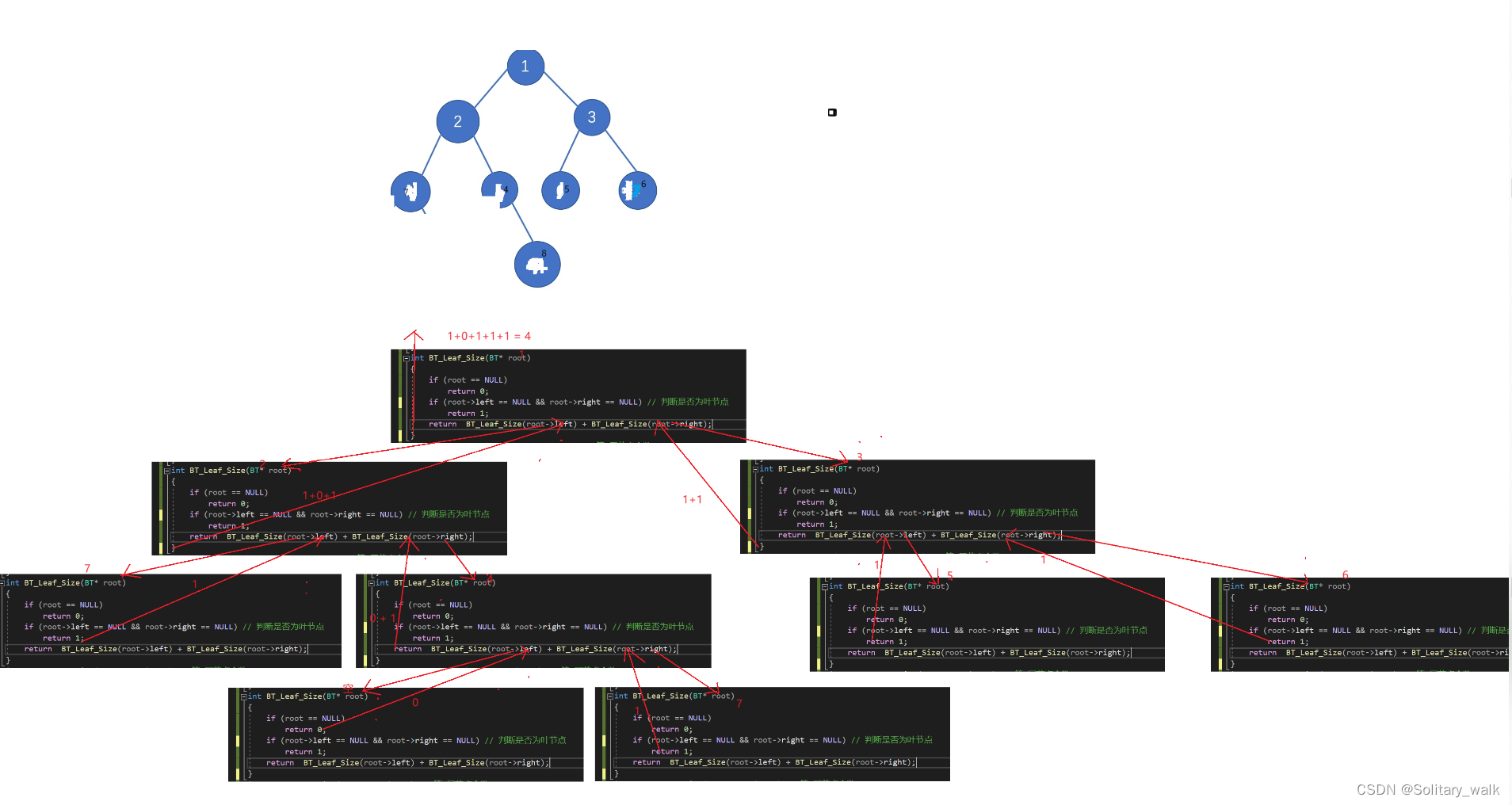

?代碼：

int BT_Leaf_Size(BT* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL) // 判斷是否為葉節點return 1;return  BT_Leaf_Size(root->left) + BT_Leaf_Size(root->right);
}

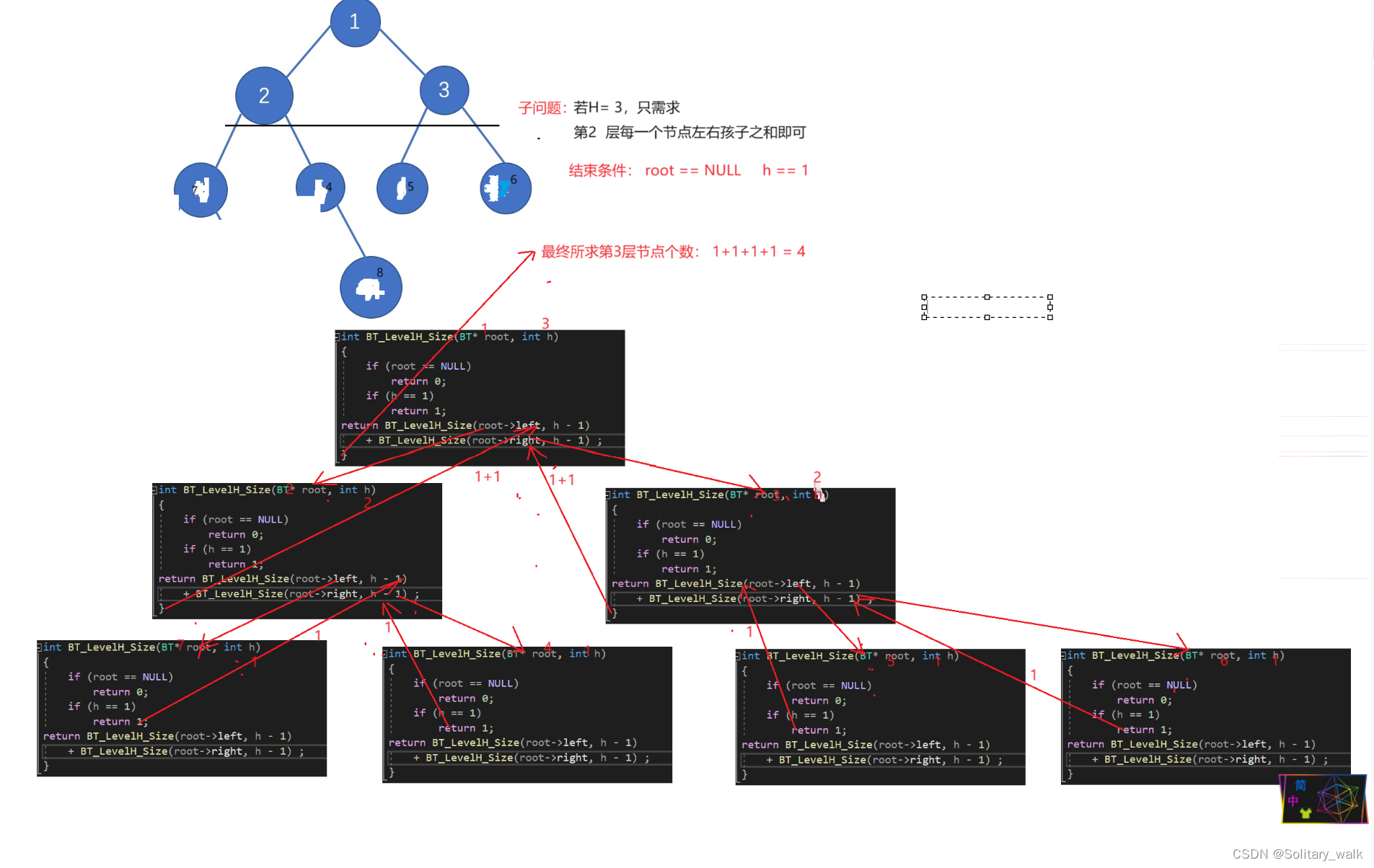
3.3求二叉樹第H層節點個數

假設根節點所在層次就是第一層，依次下推，第H層的每個節點必然是第（H-1）層節點的左右孩子，這不就解決問題了嘛：求二叉樹第H層節點個數轉化為求二叉樹第H-1層每個節點的左右孩子之和不就OK了。

?分析見下：

?代碼：

int BT_LevelH_Size(BT* root, int h)
{if (root == NULL)return 0;if (h == 1)return 1;
return BT_LevelH_Size(root->left, h - 1)+ BT_LevelH_Size(root->right, h - 1) ;
}

4.二叉樹高度的求解

對于一個二叉樹而言，樹的高度是左子樹與右子樹相比高度最大的一個再加1

還是如此，借助遞歸思想

子問題：左子樹與右子樹相比高度最大的一個再加1

結束條件：判斷當前節點是否為空，其次當前節點是否為葉節點

?分析見下：

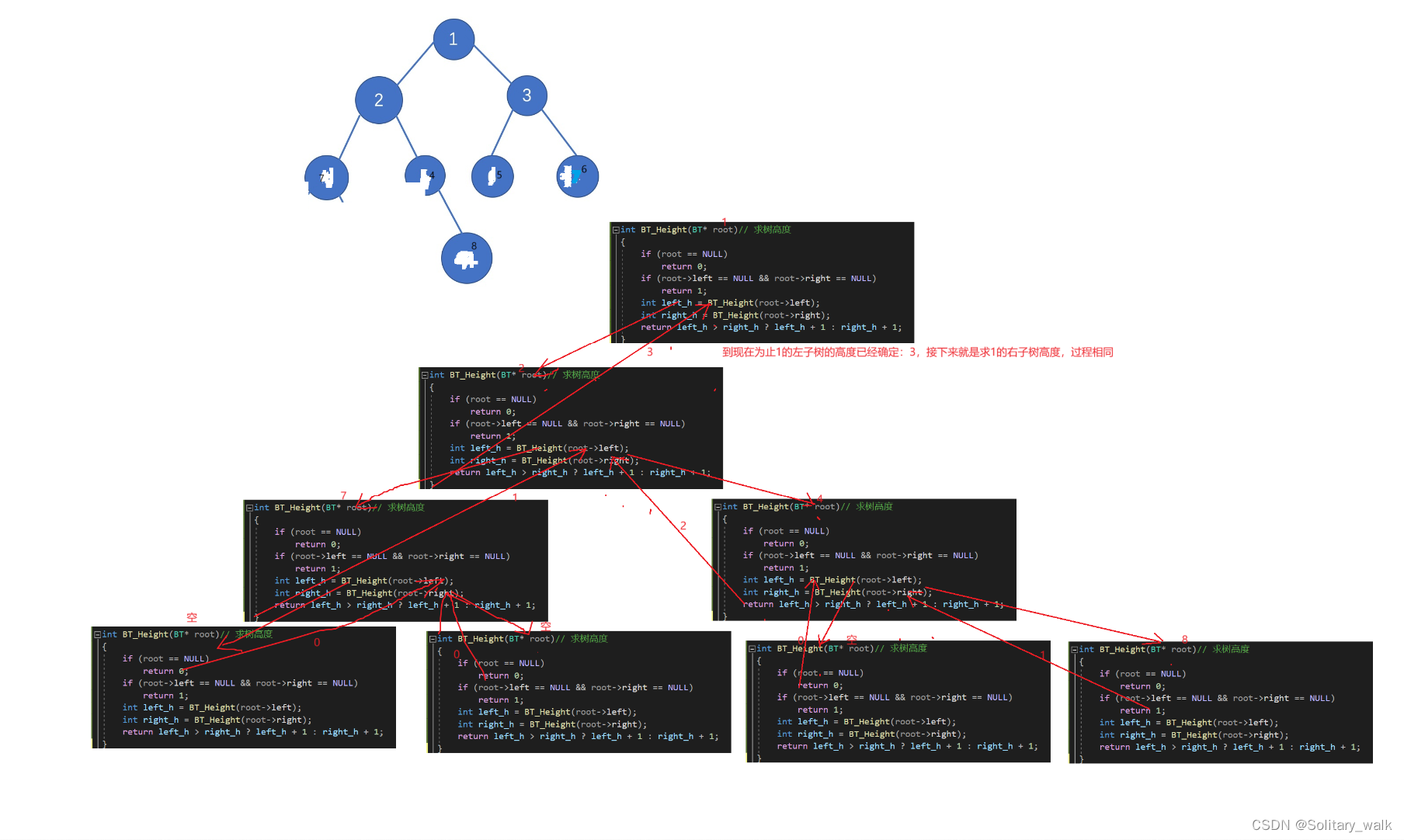
代碼：

int BT_Height(BT* root)// 求樹高度
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;int left_h = BT_Height(root->left);int right_h = BT_Height(root->right);return left_h > right_h ? left_h + 1 : right_h + 1;
}

5.二叉樹的銷毀

注意這是鏈式二叉樹，不能直接進行刪除，更為直接的是采用后續遍歷來進行銷毀

代碼：

void BT_Destroy(BT* root)
{if (root == NULL)return;BT_Destroy(root->left);BT_Destroy(root->right);free(root);
}

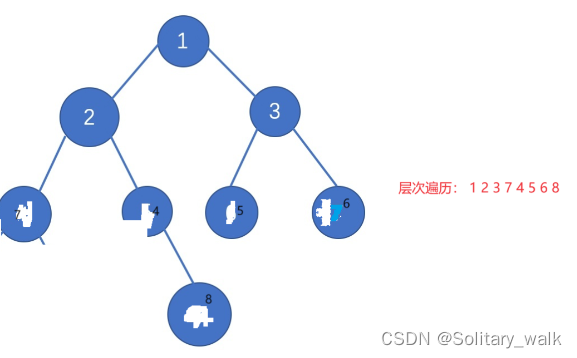
6.二叉樹的層次遍歷

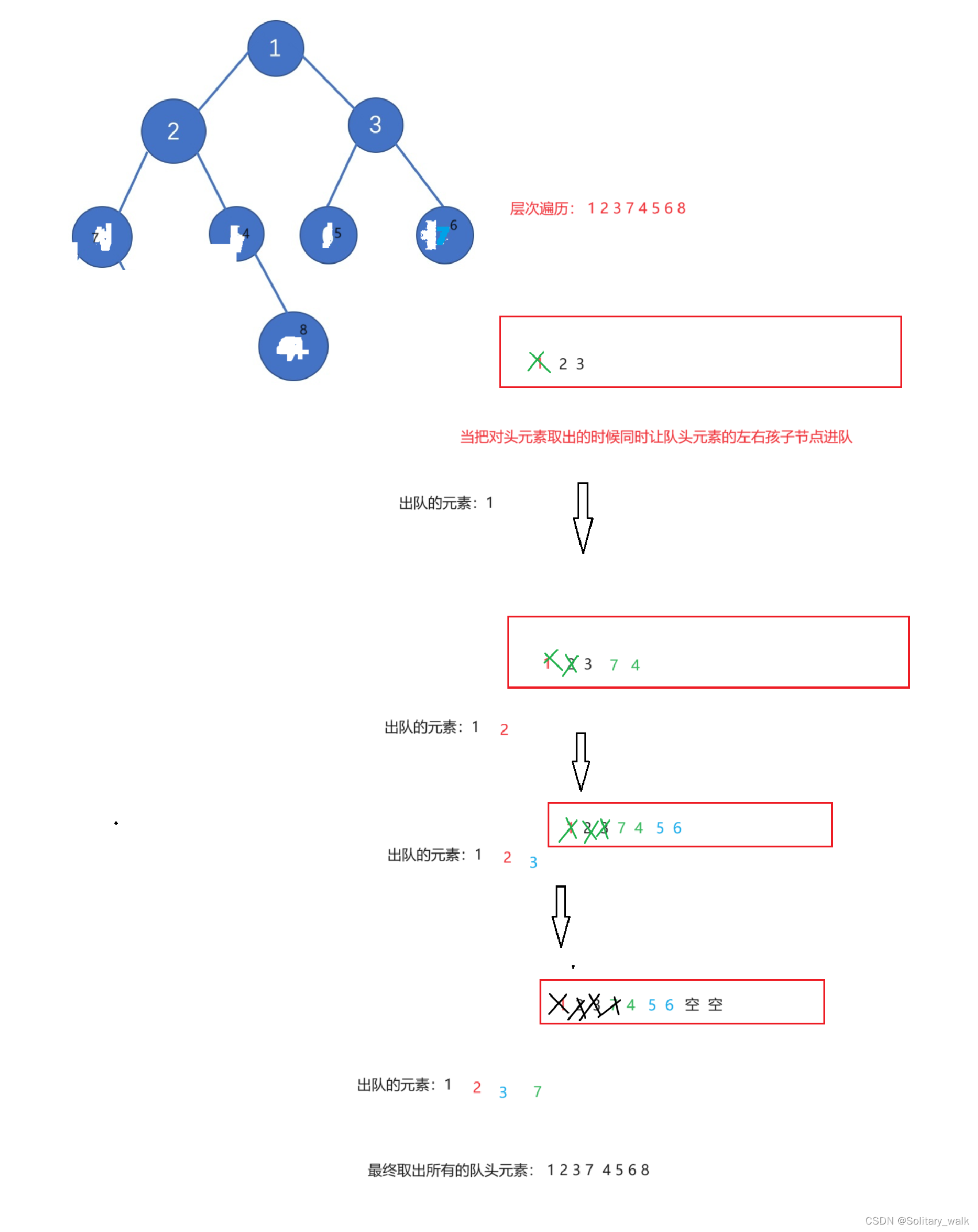
?對于二叉樹的層次遍歷很顯然就是一層一層進行遍歷，在這里借助隊的性質先進先出，來實現對二叉樹的層次遍歷

當隊頭元素出隊的時候同時讓隊頭元素的左右孩子節點也進隊

?這里需要借助咱們之前寫的隊列的相關代碼才可以玩喲！

?代碼：

void Level_order(BT* root)
{Queque q;QuqueInit(&q);QuquePush(&q, root);while (!QuequeEmpty(&q)){BT* front = QuequeFront(&q);//取隊頭元素if (front)printf("%d ", front->val);QuquePop(&q);//刪除隊頭元素//隊頭元素的左右孩子進隊if (front)  {QuquePush(&q, front->left);QuquePush(&q, front->right);}}QuqueDestroy(&q);
}

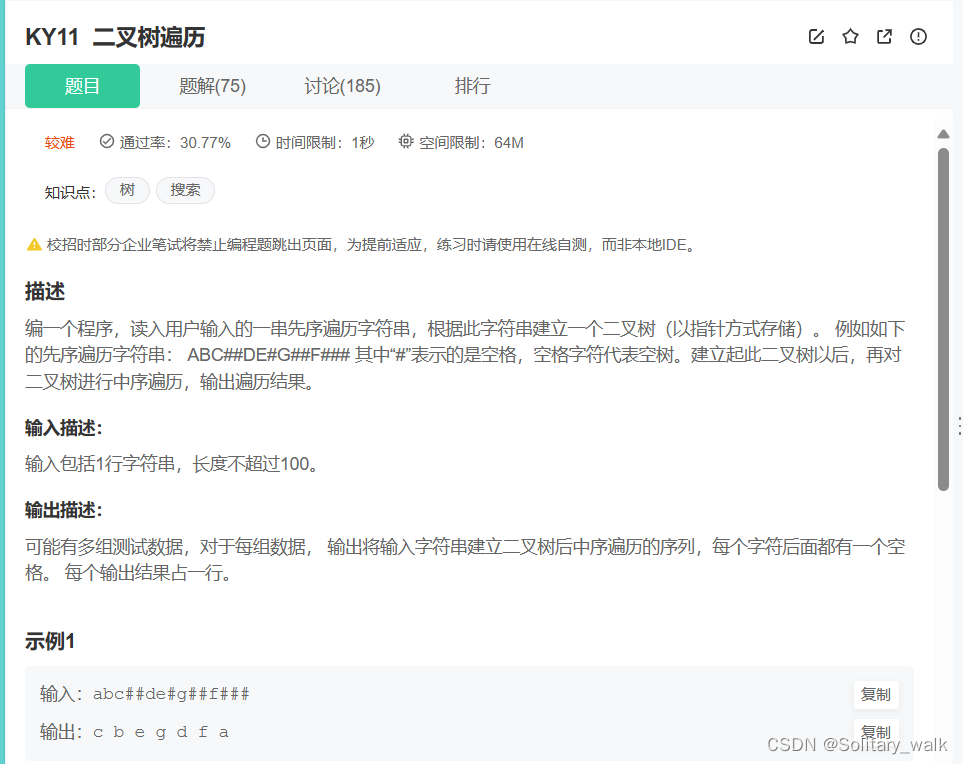
7.借助二叉樹前序遍歷的結果實現對二叉樹的構建

?分析：?還是分治的思想，層層遞歸，直到遇到空返回，把每一個節點看作一個新的根節點,只要當前節點不為空，就繼續先序遍歷

首先這是一個IO型的，所以完全需要自己手撕代碼，

先把當前字符串的內容進行接收

其次利用遞歸：先序建立二叉樹

子問題：先序建立? ? 結束條件:遇到空，直接返回

最后利用遞歸寫一個中序遍歷

?輔助：需要我們每一個數據開辟節點

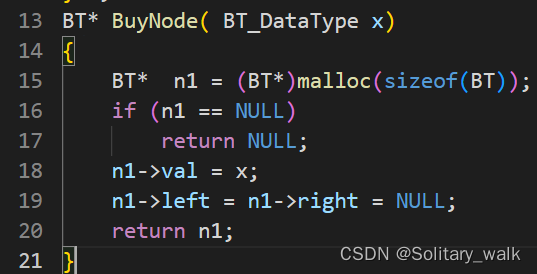
?定義一個二叉樹的結構體：

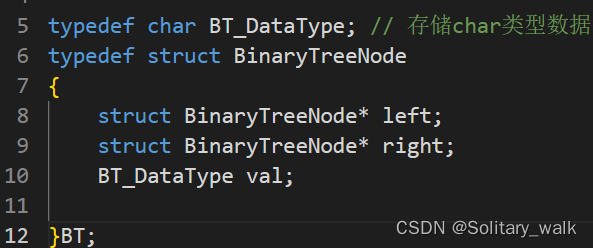
?遞歸建立二叉樹：

注意這里必須是 （*pi）++,不能是 *pi++。因為是遞歸調用每一次都需要進行棧幀建立，這樣就不能做保證下標正確性，問題本質同二叉樹求節點個數中的size

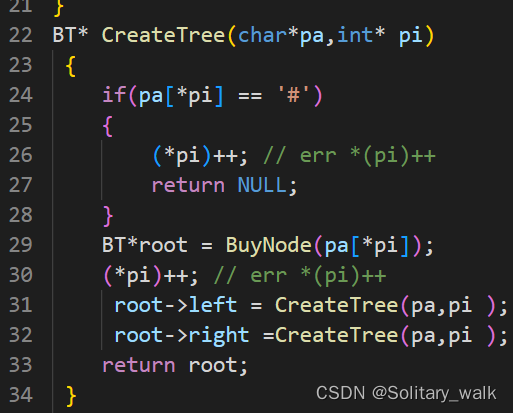
?完整代碼：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef char BT_DataType; // 存儲char類型數據
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BT_DataType val;}BT;
BT* BuyNode( BT_DataType x)
{BT*  n1 = (BT*)malloc(sizeof(BT));if (n1 == NULL)return NULL;n1->val = x;n1->left = n1->right = NULL;return n1;
}
BT* CreateTree(char*pa,int* pi){if(pa[*pi] == '#'){(*pi)++; // err *(pi)++return NULL;}BT*root = BuyNode(pa[*pi]);(*pi)++; // err *(pi)++root->left = CreateTree(pa,pi );root->right =CreateTree(pa,pi );return root;}void  In_Order(BT*root){if(root == NULL)return ;In_Order(root->left);printf("%c ",root->val);In_Order(root->right);}int main() 
{char a[100];scanf("%s",a);int i = 0;// 下標訪問數組BT* root =  CreateTree(a,&i);In_Order(root);
}

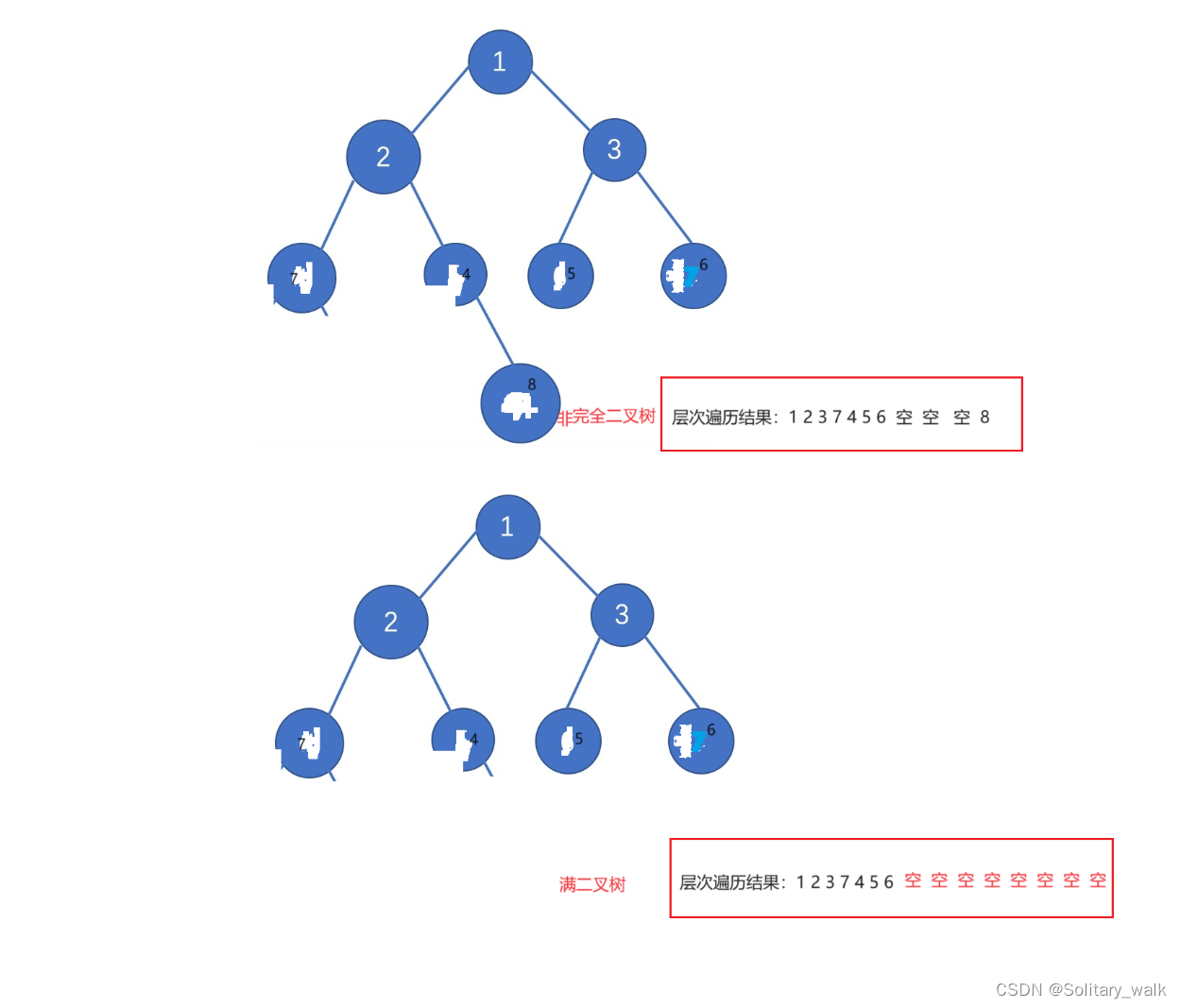
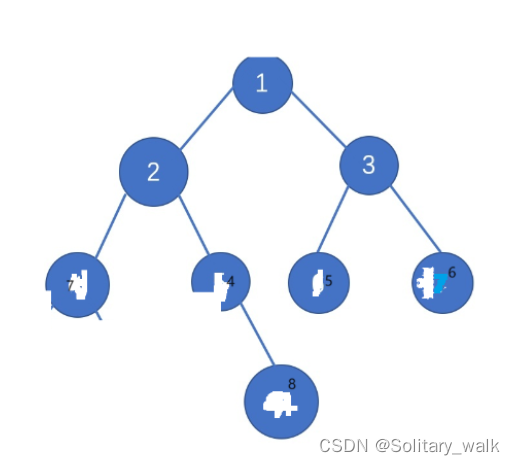
8.判斷一棵樹是否為完全二叉樹

?對于這個，可以借助層次遍歷的思想來玩。只要是在出隊的時候連續全部為空即為完全二叉樹；否則就不是完全二叉樹

?

代碼：

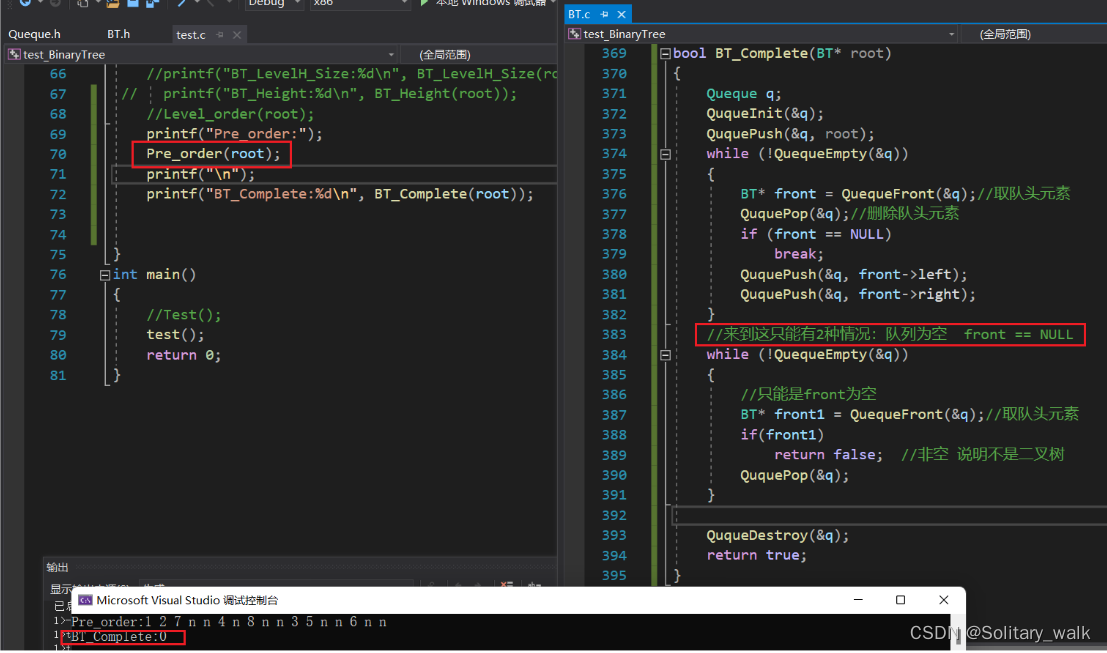
bool BT_Complete(BT* root)
{Queque q;QuqueInit(&q);QuquePush(&q, root);while (!QuequeEmpty(&q)){BT* front = QuequeFront(&q);//取隊頭元素QuquePop(&q);//刪除隊頭元素if (front == NULL)break;QuquePush(&q, front->left);QuquePush(&q, front->right);}//來到這只能有2種情況：隊列為空  front == NULLwhile (!QuequeEmpty(&q)){//只能是front為空BT* front1 = QuequeFront(&q);//取隊頭元素if(front1)return false;  //非空 說明不是二叉樹QuquePop(&q);}QuqueDestroy(&q);return true;
}

9：二叉樹的查找

查找某個節點的值是否存在，若存在則返回該節點的地址，否則返回NULL

可以用先序來遍歷

?錯誤示例：當我想查找3這個節點時候

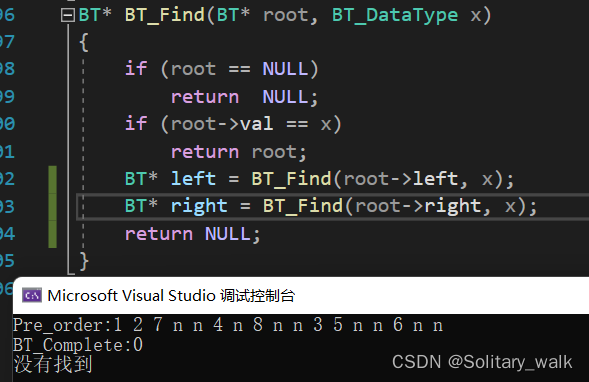
?相信有不少老鐵們一開始就會這樣寫吧，但是明明3這個節點存在為什么會沒有找到呢？

其實通過我們調試發現這樣寫的邏輯是有Bug的，及時當要查找的節點存在時，也會造成把已找到的節點覆蓋掉，其實這個查找邏輯的代碼重在對return 返回的考察

正確代碼：

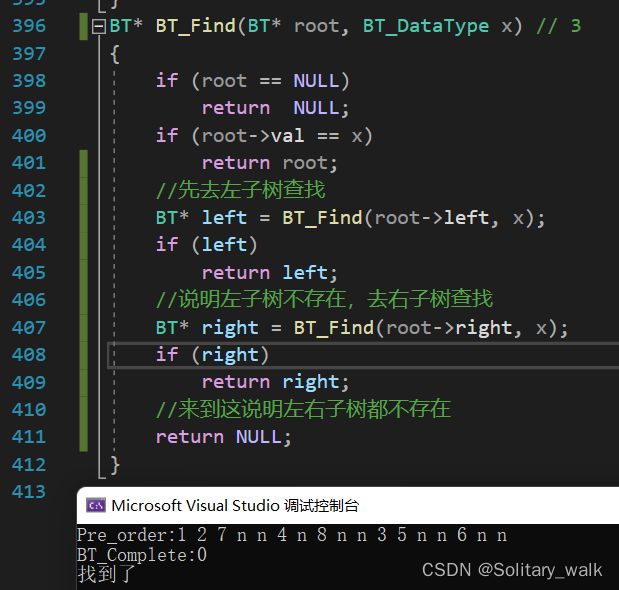
BT* BT_Find(BT* root, BT_DataType x) // 3
{if (root == NULL)return  NULL;if (root->val == x)return root; //先去左子樹查找BT* left = BT_Find(root->left, x);if (left)return left;//說明左子樹不存在，去右子樹查找BT* right = BT_Find(root->right, x);if (right)return right;//來到這說明左右子樹都不存在return NULL;
}

?運行結果：

10.二叉樹相關OJ的練習

10.1 單值二叉樹

?解題分析：

其實一個遍歷就直接搞定了。拿雙親節點的值與孩子節點對應的值進行比較，若是不相等直接 return false

是不是看著比較簡單，但是寫起來是有坑滴！

?

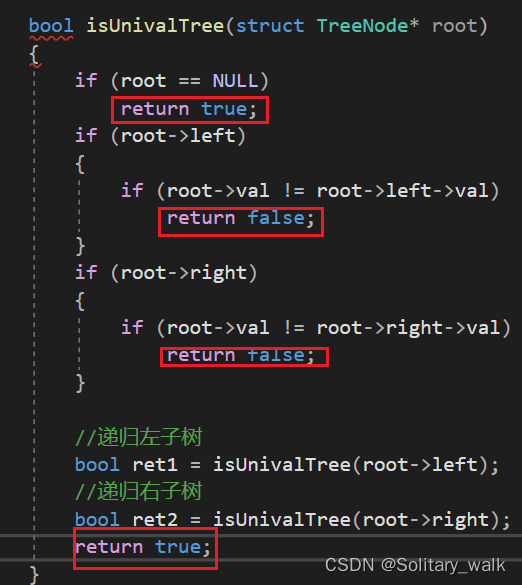
?運行結果：

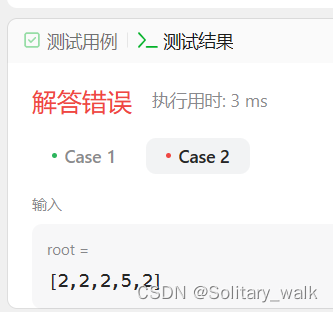
其實走讀一遍代碼大概就找到問題所在了：return 語句返回是返回到調用當前函數的上一個函數里，并不是直接返回到最外層?

這個問題的本質同二叉樹查找指定數據是一樣的

OJ代碼：

bool isUnivalTree(struct TreeNode* root) 
{if(root == NULL)return true;if(root->left){if(root->val != root->left->val)return false;}if(root->right){if(root->val != root->right->val)return false;}//遞歸左子樹bool ret1 = isUnivalTree(root->left);//遞歸右子樹bool ret2=  isUnivalTree(root->right);return ret1 && ret2;
}

10.2 判斷2個二叉樹是否相同

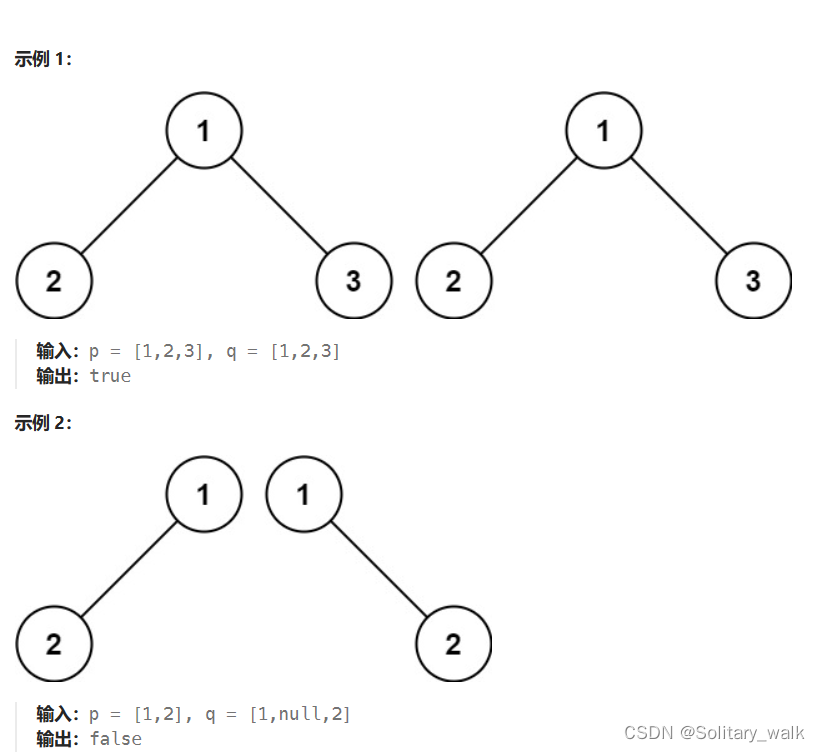
?解題分析：

采用遍歷的方式，根節點與根節點進行對比，左孩子與左孩子對比，右孩子與右孩子對比，注意是對比val而不是對比節點所對應的地址

OJ代碼：

bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL &&q == NULL)return true;if(p == NULL || q == NULL)return false;//來到這說明都不為空if(p->val  != q->val)return false;return  isSameTree(p->left,q->left) && isSameTree(p->right,q->right);//注意這里必須是 邏輯且的關系，不能是邏輯或
}

?OK，以上就是我今日要為大家分享的，希望各位都有得！對于二叉樹這部分是數據結構初階比較難的一部分了，初學的時候是不好理解，事事都有個過渡期，當然自己有空的時候也不要忘了敲敲代碼！