卷積（convolution）、通道（channel）

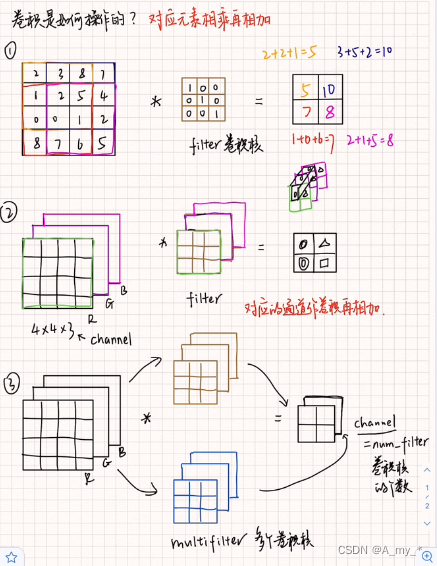
步長（stride）、填充（padding）

卷積核移動的步長（stride）小于卷積核的邊長（一般為正方行）時，便會出現卷積核與原始輸入矩陣作用范圍在區域上的重疊（overlap），卷積核移動的步長（stride）與卷積核的邊長相一致時，不會出現重疊現象。

舉例：

填充（padding，在原始input的周圍進行填充），以保證卷積后的大小與原始 input shape 一致。

定量計算公式：

補零填充（zero padding）：保證卷積后的大小與原始尺寸一致

K為卷積核的大小（K通常是奇數），這樣如果原始 input 的大小為 w*w，填充后的大小為 (w+k-1)*(w+k-1)（兩端都要填充）

卷積后的大小：

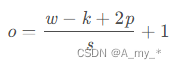
其中,w： input 的 height/width；k：卷積核的 height/width；p：表示填充的大小；s：stride 步長；

舉例：

7*7 的 input，3*3 的 kernel，無填充，步長為1，則 o = （7-3）/1 +1=5，也即 output size 為 5*5

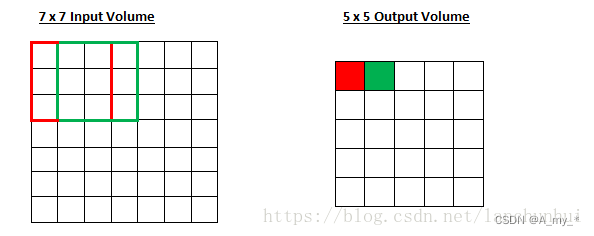
7*7 的 input，3*3 的 kernel，無填充，步長為2，則 o =(7-3)/2+1=3，也即 output size 為 3*3

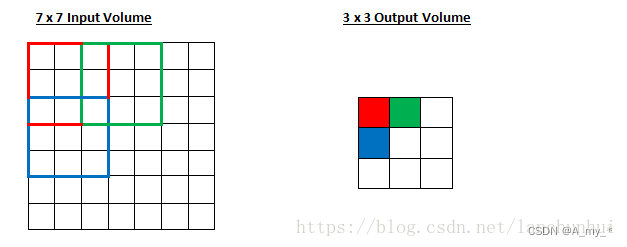
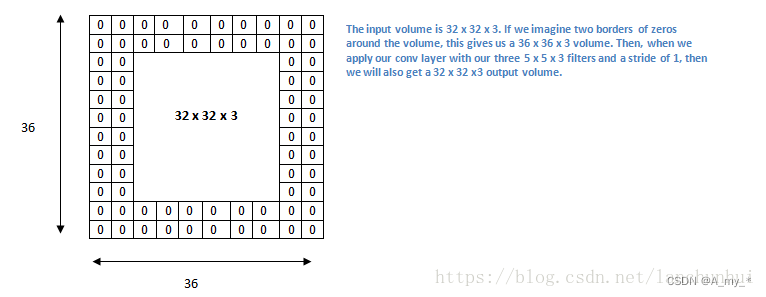
感受野

感受野指的是卷積神經網絡每一層輸出的特征圖(feature map)上每個像素點映射回輸入圖像上的區域大小。第一層卷積層的輸出特征圖像素的感受野大小等于卷積核的大小，其它卷積層的輸出特征圖的感受野的大小和它之前所有層的卷積核大小和步長都有關。神經元感受野的范圍越大表示其能接觸到的原始圖像范圍就越大，也意味著它能學習更為全局，語義層次更高的特征信息，更能檢測出大目標，相反，范圍越小則表示其所包含的特征越趨向局部和細節（比如說位置或者顏色）。因此感受野的范圍可以用來大致判斷每一層的抽象層次，并且我們可以很明顯地知道網絡越深，神經元的感受野越大。

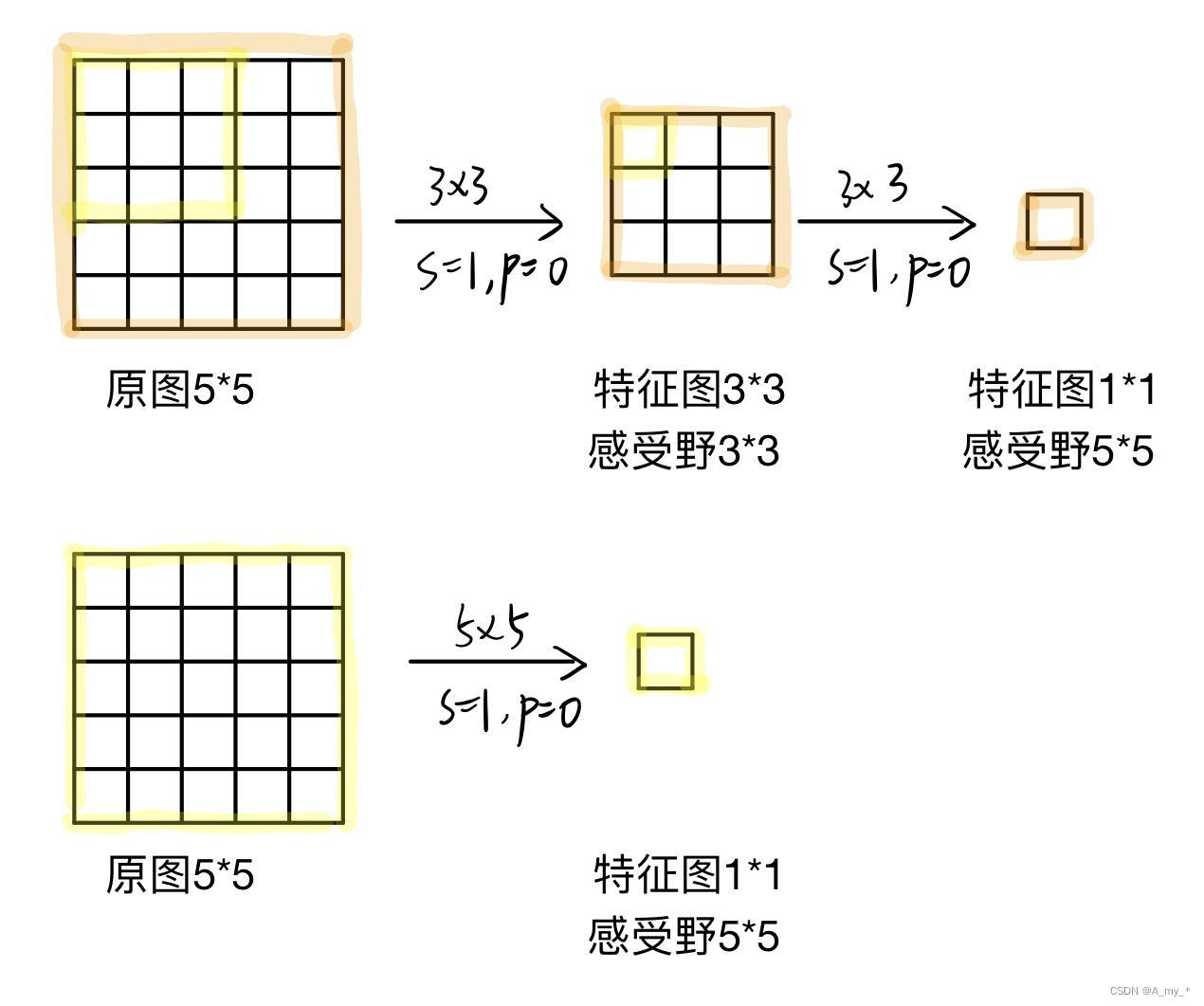
VGG使用上圖第一種方法，用多個3*3卷積核堆疊代替大的卷積核（5*5）來減少參數量。

解釋：設原圖大小h*w*c，卷積后通道數保持不變（如本文第一張圖的圖③，卷積后通道數為2，原圖通道數為3，要使卷積后通道數保持不變應再加一組卷積核，即卷積核組數=原圖通道數），計算卷積核參數的數量：

2個3*3：（3*3*c）*c*2=18c^2

1個5*5：（5*5*c）*c=25c^2

由此可見，得到相同大小的特征圖和感受野，用多個3*3卷積核堆疊代替大的卷積核（5*5），參數量有所下降。而且由于是多個卷積層的堆疊，每個卷積層后都加relu激活，那么提取出來特征的非線性就更強

卷積核：k*k，k太大會增加后續的計算量且信息抽象層次不夠高，影響網絡性能，k太小會造成非常嚴重的信息丟失，如原始分辨率映射到最后一層的feature map有效區域可能不到一個像素點，使得訓練無法收斂。k一般為奇數，有中心像素點，便于定位卷積核。

計算每一層特征圖的感受野：

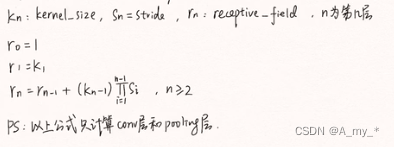
舉例：

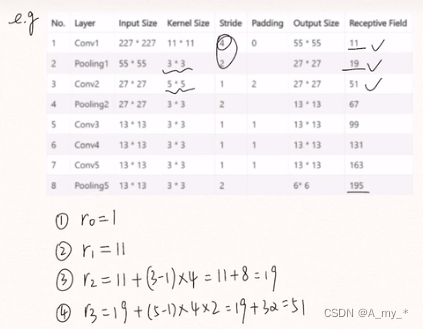
反卷積

為了更深度的了解反卷積，現在還來看下卷積的數學操作。

1、卷積的數學操作

如果把卷積操作寫成矩陣相乘，則對于4 ? 4的輸入和3 ? 3的卷積核的結果如下：

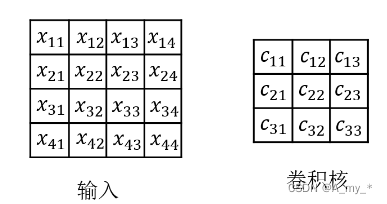
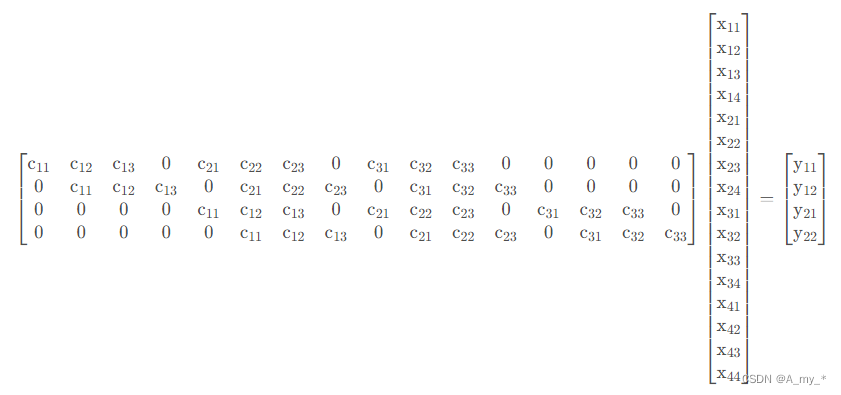
最后得到一個4 ? 1的矩陣，可以reshape成2 ? 2的矩陣，便是最后卷積的結果，即y=cx

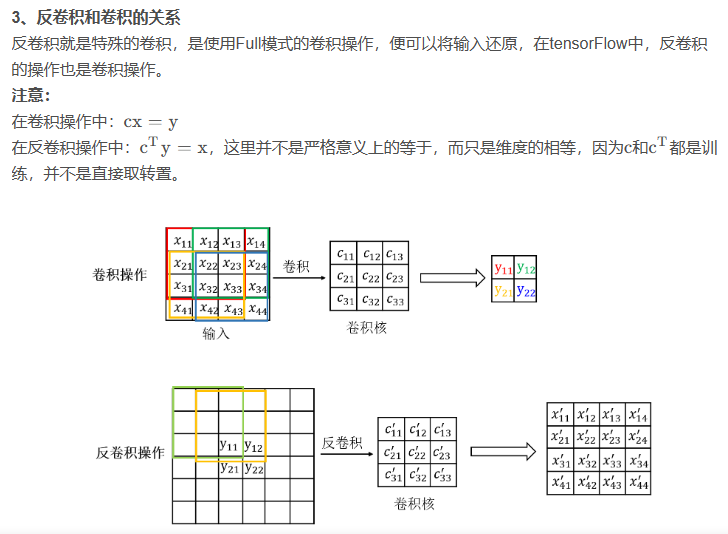
參考1

參考2

參考3