1、曲線的連續性

曲線的連續性是三維建模、動畫設計等領域中非常重要的一個概念，它涉及到曲線在不同點之間的連接方式和光滑程度。下面將詳細介紹曲線的連續性，包括C連續性和G連續性。

1.1C連續性（參數連續性）

C連續性是指曲線在參數空間中的連續性。在參數空間中，曲線的連續性可以通過匹配相鄰曲線段在連接點處的參數導數來實現。C連續性的級別用C0、C1、C2、C3等來表示，其中數字表示導數的階數。

C0連續性：這是最基本的連續性要求，它只要求曲線在連接點處沒有斷開，即幾何位置連續。C0連續性保證了曲線在連接點處是連續的，但沒有考慮到切線方向、曲率等更高級別的信息。

C1連續性：在滿足C0連續性的基礎上，C1連續性要求曲線在連接點處的切線方向相同，即曲線的斜率連續。這意味著曲線在連接點處不僅是連續的，而且在該點處的切線方向也是連續的。C1連續性提供了比C0連續性更高的平滑度要求。

C2連續性：C2連續性要求曲線在連接點處的曲率連續，即曲線在連接點處的曲率變化率也是連續的。這提供了比C1連續性更高的平滑度要求，使得曲線在連接點處更加平滑。

C3連續性：這是最高級別的參數連續性，它要求曲線在連接點處的曲率變化率的導數也是連續的。C3連續性提供了非常平滑的曲線過渡，使得曲線在視覺上更加自然。

1.2G連續性（幾何連續性）

G連續性是指曲線在幾何空間中的連續性。在幾何空間中，曲線的連續性可以通過匹配相鄰曲線段在連接點處的幾何信息來實現。G連續性的級別用G0、G1、G2、G3等來表示，其中數字表示導數的階數。

G0連續性（位置連續性）：G0連續性要求新構造的曲線直接連接兩個端點，即曲線在連接點處的位置連續。這是最基本的幾何連續性要求，它只保證了曲線在連接點處沒有斷開。

G1連續性（相切連續性）：在滿足G0連續性的基礎上，G1連續性要求新構造的曲線在連接點處與相鄰曲線段相切，即曲線在連接點處的切線方向相同。G1連續性提供了比G0連續性更高的平滑度要求，使得曲線在連接點處更加平滑。

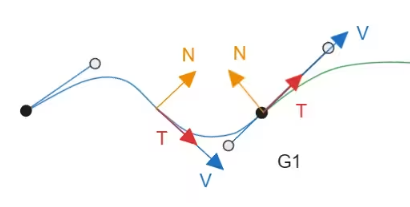
G2連續性（曲率連續性）：G2連續性要求在滿足G1連續性的基礎上，新構造的曲線在連接點處的曲率相同。這意味著曲線在連接點處不僅切線方向相同，而且曲率也相同。G2連續性提供了比G1連續性更高的平滑度要求，使得曲線在連接點處更加自然。

G3連續性（流連續性）：這是最高級別的幾何連續性，它要求新構造的曲線在連接點處的曲率變化率也相同。G3連續性提供了非常平滑的曲線過渡，使得曲線在視覺上更加自然和流暢。

2、曲面連續性

曲面的連續性是三維建模和幾何造型中的重要概念，它描述了曲面在不同點之間的連接方式和光滑程度。曲面的連續性可以分為多個級別，從最低的位置連續性（G0）到最高的流連續性（G3），每個級別都對曲面的光滑度和連續性有不同的要求。下面將詳細全面介紹曲面的連續性。

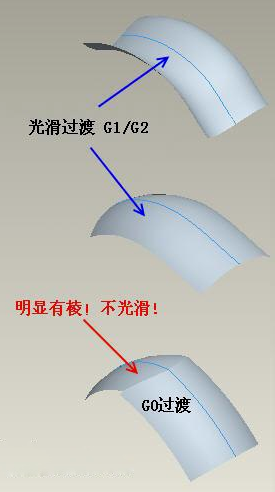
位置連續性（G0）

位置連續性是曲面連續性的最低要求。在G0連續性的條件下，新構造的曲面與相鄰的曲面在連接處沒有斷開，即它們的位置是連續的。換句話說，兩個曲面在相交線處可以直接連接起來，而不需要在相交線處相切。這種連續性的要求相對較低，因此在實際應用中很容易實現。

相切連續性（G1）

相切連續性是在位置連續性的基礎上更高的要求。在G1連續性的條件下，新構造的曲面與相鄰的曲面在相交線處不僅位置連續，而且它們的法線方向相同，即它們在該點處相切。這意味著兩個曲面在連接處具有相同的切線方向，使得曲面在視覺上更加平滑。G1連續性對于創建高質量的模型非常重要，特別是在需要平滑過渡的場景中。

曲率連續性（G2）

曲率連續性是在相切連續性的基礎上更高的要求。在G2連續性的條件下，新構造的曲面與相鄰的曲面在相交線處不僅位置連續、法線方向相同，而且它們的曲率也相同。這意味著兩個曲面在連接處的形狀和彎曲程度都是連續的，從而提供了更加平滑和自然的過渡效果。G2連續性在創建高質量的模型和動畫中非常重要，特別是在需要高度真實感和自然度的場景中。

流連續性（G3）

流連續性是曲面連續性的最高要求。在G3連續性的條件下，新構造的曲面與相鄰的曲面在相交線處不僅滿足上述所有條件，而且它們的曲率變化率也相同。這意味著兩個曲面在連接處的形狀、彎曲程度和速度變化都是連續的，從而提供了非常平滑和自然的過渡效果。G3連續性在創建高質量的模型和動畫中非常重要，特別是在需要高度真實感和自然度的場景中。

Open CASCADE在 GeomAbs_Shape 枚舉類型描述了曲線和曲面支持的連續性的類型。

enum GeomAbs_Shape{GeomAbs_C0,GeomAbs_G1,GeomAbs_C1,GeomAbs_G2,GeomAbs_C2,GeomAbs_C3,GeomAbs_CN};

C0 (GeomAbs_C0) —— 參數連續性。它與G0(幾何連續性)是一致的，所以G0沒有單獨變量表示。

G1(GeomAbs_G1) —— 左曲線的切向量和右曲線的切向量是平行的。

C1(GeomAbs_C1) —— 暗示一階導的連續性

G2(GeomAbs_G2) —— 在G1連續的基礎上，左曲線和右曲線的曲率中心是相同的

C2(GeomAbs_C2) —— 一直到二階導都是連續的

C3(GeomAbs_C3) —— 一直到三階導都是連續的

CN(GeomAbs_CN) —— 一直到N階到都是連續的(連續的無窮階)