題目描述

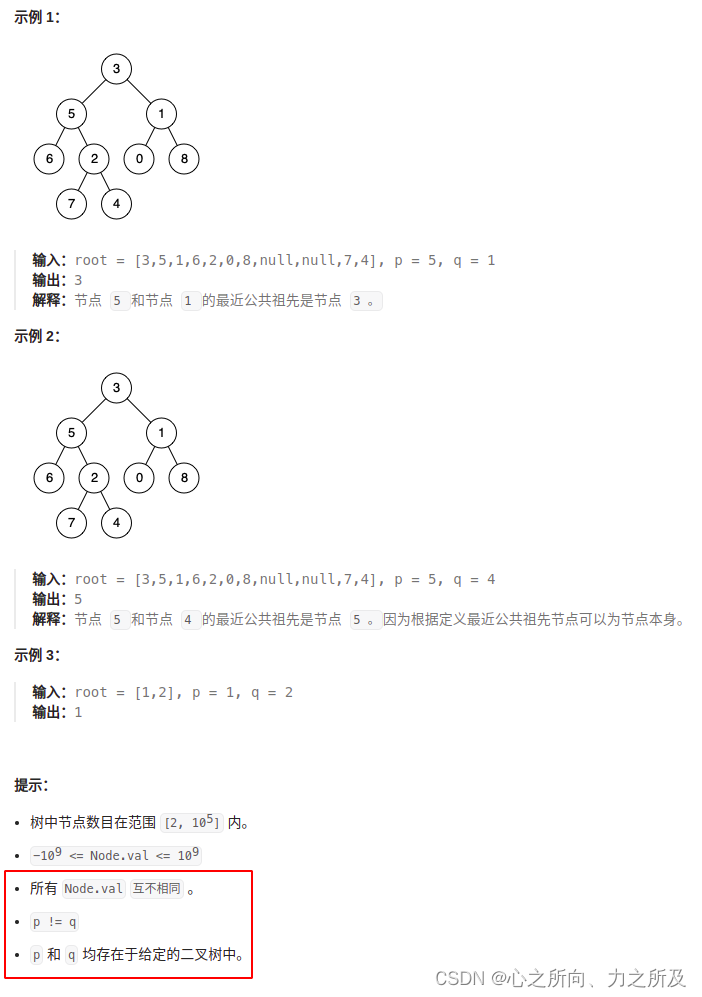
給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義為：“對于有根樹 T 的兩個節點 p、q，最近公共祖先表示為一個節點 x，滿足 x 是 p、q 的祖先且 x 的深度盡可能大（一個節點也可以是它自己的祖先）。”

題目分析

1. 首先需要注意下提示信息：
   a. 二叉樹中所有節點中的值互不相同；
   b. p不等于q;
   c. p和q均存在于給定的二叉樹中。
2. 根據題意可知，若node節點為p,q的最近公共祖先，則可能的情況如下：
   a. p 和 q分別在node的左右子樹中；
   b. p = node, 且q在node的左/右子樹中；
   c. q = node，且p在node的左/右子樹中。
3. 從根節點開始遍歷，遞歸向左右子樹進行遍歷；
   a. 遞歸結束條件：當前查詢節點為null，或者當前節點為p或q，則返回當前節點
   b. 遞歸邏輯，結合2中的情況分析：
   遞歸遍歷當前節點的左右子樹，如果左右子樹返回的節點都不為空，則表明p和q分別在左右子樹中，即當前節點為最近公共祖先。
   如果左右子樹返回節點其中一個不為空，則返回非空節點。

Code

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (nullptr == root || p == root || q == root) {return root;}TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p , q);if (nullptr == left) {return right;}if (nullptr == right) {return left;}return root;}
};